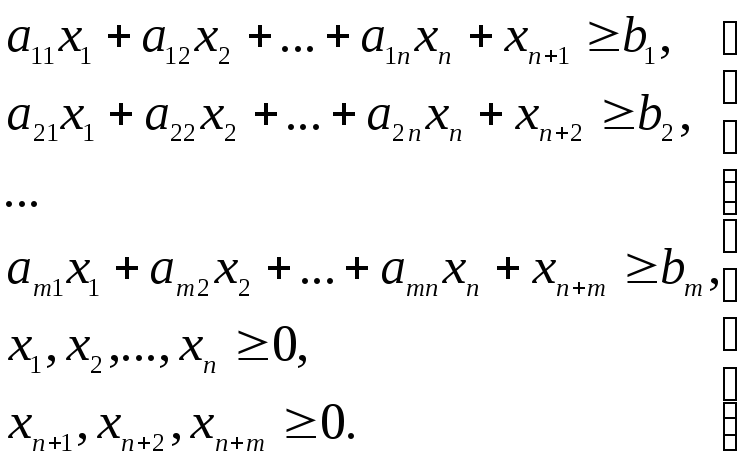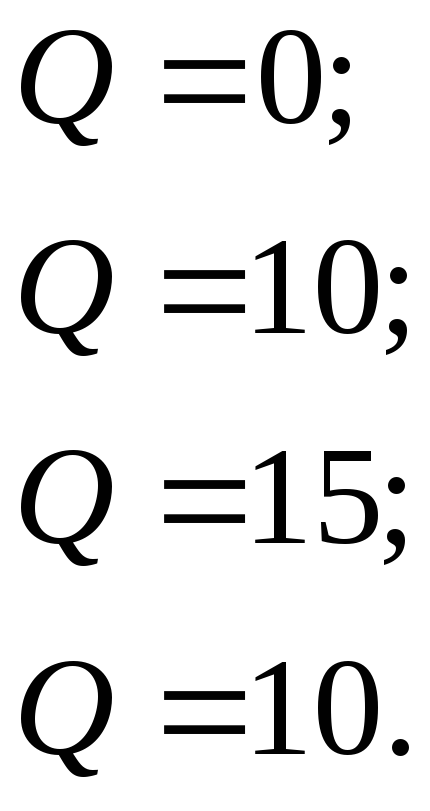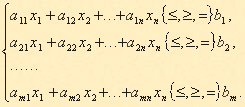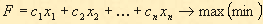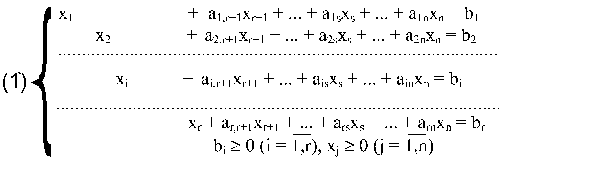Общая задача линейного программирования стандартный вид

6. Постановка задач линейного программирования. Примеры, различные формы задач и подходы решения. Постановка задач линейного программирования

Линейное программирование — область математики, разрабатывающая теорию и численные методы решения задач нахождения экстремума (максимума или минимума) линейной функции многих переменных при наличии линейных ограничений, т. е. равенств или неравенств, связывающих эти переменные.

В общей постановке задача линейного программирования (ЗЛП) формулируется следующим образом. Имеются какие-то переменные x = (x1, x2,…, xn) и линейная функция этих переменных, которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции при условии, что переменные x удовлетворяют системе линейных равенств и/или неравенств.

Функция цели в задаче линейного программирования обычно записывается так:

Или в сокращённом виде с сигмой:

Можно встретить обозначение целевой функции и через C, и через F.

Система ограничений в задаче линейного программирования в канонической форме записывается так:

И система ограничений, и целевая функция имеют линейный характер, то есть содержат переменные только в первой степени.

Целевая функция. Её нужно максимизировать или минимизировать. Для того, чтобы функцию максимизировать, переменные, являющиеся её слагаемыми, должны принимать как можно большие значения в соответствии с условиями задачи. При минимизации — наоборот, меньшие. Обычно целевая функция выражает доходы или расходы.

Переменные. Каждая переменная, как правило, означает запасы одного из производственных факторов — вида сырья, времени, рабочей силы, технологических возможностей или чего-либо другого.

Ограничения. Очень просто. Например, в каждом уравнении (неравенстве) заданы ограничения перечисленных выше или других запасов, используемых для производства определённого вида продукции.

Примеры, различные формы задач и подходы решения

Задача линейного программирования математически может быть представлена в различных формах.

Общей задачей ЛП называется задача, которая состоит в определении максимального (минимального) значения функции

Помимо общей формы, различают еще две частные задачи линейного программирования — стандартную и основную.

Особенностью стандартной задачи ЛП является то, что ее ограничения представлены в виде линейных неравенств, а также условий неотрицательности на переменные, присутствующие в задаче:

Ограничения основной задачи ЛП представляют собой линейные ограничения-равенства, а также условия неотрицательности на переменные:

Задачи линейного программирования в случае двух переменных можно решить и графическим методом, в случаях, когда переменных больше, применяется симплекс-метод.

Примеры решения задач линейного программирования:

Пример №1. Предприятие выпускает продукцию двух разновидностей. Каждый вид продукции проходит обработку на трёх станках. При обработке 1 т продукции I вида первый станок используется 0 ч, второй станок – 1 ч, третий станок – 1 ч. При обработке 1 т продукции II вида первый станок используется 1 ч, второй станок – 4 ч, третий станок – 1 ч. Время работы станков ограничено и не может превышать для первого станка 7 ч, для второго 29 ч, для третьего 11 ч. При реализации 1 т продукции I вида предприятие получает прибыль 2 руб., а при реализации 1 т продукции II вида – 5 руб. Найти оптимальный план выпуска продукции каждого вида, дающий максимальную прибыль от реализации всей продукции.

3. Решим прямую задачу графически:

Источник

2. Линейное программирование

К задачам линейного программирования относятся такие оптимизационные задачи, в которых и целевая функция и ограничения – линейный многочлен.

2.1. Стандартный вид задачи линейного программирования (злп)

В стандартном виде ЗЛП целевая функция минимизируется, ограничения имеют вид равенств:

(2.1)

Здесь a_ij, b_i, p_i – постоянные коэффициенты.

В этих задачах количество переменных больше или равно количеству ограничений-равенств: n≥m.

Если n  m, то область допустимых решений – точка;

если n  m, то область допустимых решений – многогранник;

если n  m, то (m – n) ограничений линейно зависимы и их можно исключить.

2.2. Способы приведения задачи линейного программирования к стандартному виду

Случай 1. Исходные условия задачи: целевая функция минимизируется, ограничения представляют систему неравенств вида «меньше или равно».

Для приведения задачи к стандартному виду вводят искусственные переменные . Эти искусственные переменные прибавляют к левым частям ограничений:

(2.2)

Полученная задача тождественна исходной. Действительно, убрав искусственные переменные, получим левые части ограничений  b_i.

Случай 2. Исходные условия задачи: целевая функция минимизируется, ограничения имеют вид неравенств типа «больше или равно»:

Аналогично предыдущему случаю вводятся искусственные переменные, но эти переменные вычитаются из левых частей ограничений.

Случай 3. Исходные условия задачи: целевая функция максимизируется, ограничения имеют вид равенств.

Для приведения задачи к стандартному виду (2.1) сменим целевую функцию на целевую функциюG, все коэффициенты которой помножены на –1: Полученная задача тождественна исходной.

2.3. Графический метод решения задач линейного программирования

Графический метод применяется для решения задач небольшой размерности (количество переменных не превышает 3). Рассмотрим метод на примере решения следующей задачи:

(2.3)

1. Ограничения-неравенства заменяются на ограничения-равенст­ва:

1. Строятся графики полученных функций:

Рис. 2.1. Графический метод решения ЗЛП

1. Находится область допустимых решений (область, где выполняются все ограничения).
2. Строится график целевой функции при каком-либо значении правой части:

1. График целевой функции перемещается параллельно самому себе в сторону роста (уменьшения при Q  min) целевой функции до касания с границей области допустимых решений. Граничная точка (или отрезок прямой) является решением задачи линейного программирования.
2. Находится решение: координаты граничной точки (точка А) и значение целевой функции в этой точке:

Выводы: 1. Область допустимых решений задачи линейного программирования представляет собой выпуклый многогранник. 2. Решение задачи линейного программирования находится на границе области допустимых решений. Способ 2. Пункты 1–3 выполняются аналогично Способу 1.

1. Подсчитываются значения целевой функции во всех вершинах допустимого многогранника.

, следовательно, точка – решение задачи. Пример 1. Способ 1.

1. Ограничения-неравенства заменяются на ограничения-равенства:

1. Строятся графики полученных функций:

Рис. 2.2. 3. Находится область допустимых решений (область, где выполняются все ограничения). 4. Строится график целевой функции при каком-либо значении правой части: 5. График целевой функции перемещается параллельно его начальному положению в сторону уменьшения целевой функции до касания с границей области допустимых решений. Отрезок прямой АВ является решением задачи линейного программирования. 6. В ответе записываются функция, граничные точки отрезка и значение целевой функции на этом отрезке: , , Способ 2. 1 – 3 пункты выполняются аналогично Способу 1.

1. Подсчитываются значения целевой функции во всех вершинах допустимого многогранника.

–в двух точках, следовательно, отрезок AB, соединяющий эти точки, является решением задачи.

Источник

11.Общая, каноническая, стандартная задача линейного программирования.

В общем виде задачи об использовании ресурсов и о диете можно записать в общем виде. Пусть дана система m линейных неравенств с n- неизвестными.

(7)

И линейная функция (8)

Необходимо найти такое решение Х=(х1,х2,…,хn) удовлетворяющее неотрицательности

При котором функция(8) принимает оптимальное (мин,мах) значение. Это задача называется ЗЛП.

Система(7) система ограниченная ЗЛП, функция (8) – целевая функция.

Допустимым решением ЗЛП называется решение Х=(х1,х2,…,хn) системы ограничении удовлетворения условиям неотрицательности.

Оптимальным решением решения ЗЛП наз-ся план х1,х2,…,хn при которой целевая функция принимает оптимальное значение. Мы рассмотрели ЗЛП в которых система ограничений состоят только из неравенств, такие ЗЛП называются СТАНДАРТНЫМИ. Но система ограничений может состоять и из линейных неравенств и из линейных уравнений – ОБЩАЯ ЗЛП. Если же система ограничений ЗЛП состоит только из уравнений то ЗЛП называют КАНОНИЧЕСКОЙ.

12. Симплексная форма злп.

Допустимое решение ЗЛП называется Базисным, если все его свободные неизвестные равны нулю, а соответствующие ему значения целевой функции f(b1,b2,…,br,0)=b0 называется базисным.

Симплексная форма ЗЛП удовлетворяет следующим требованиям: система ограничений должна быть такой что:

1. Все ограничения записаны в виде уравнений.
2. Правые части уравнений неотрицательны bi≥0, i=
3. Система состоящая из r уравнении имеет r базисных уравнений

Целевая ф-ия удовлетворяет условиям:

1. Она содержит только свободные переменные
2. Обязательная минимизация ( случай нахождения мах сводится на задаче нахождения мин по формуле махf=-minf
3. Все слагаемые целевой ф-ии перенесены влево кроме b0

13. Матричная форма симплексного метода. Критерии оптимальности плана и его отсутствия. Симплексные преобразования.

В симплексной форме ЗЛП соответствует симплексная матрица состоящая из коэффициентов при неизвестных, правых частей уравнений и функций.

Базисное решение =(в1,в2,….,в0,0…,0) и базисное значение целевой функции. При этом мы каждый раз будем получать новую симплексную матрицу. По ней можно определить является ли базисное решение оптимальным с помощью следующего критерия.

Критерий оптимальности плана.

Если в последней сторке (целевой строке) симплексной матрицы, все элементы положительны без учеты последнего в0, то соот-ии этой матрице на опорный план оптимален.

Критерий отсутствия оптимальности. Если в симплексной матрице имеется столбец в котором последний элемент Cs>0 а все остальные элементы не положительны то ЗЛП не имеет оптимального плана minf=-∞.

Если в симплексной матрице не выполняется оба критерия то в необходимо перейти к следующей матрице с помощью разрешающего элемента. ais >0. A)определяется разрешающий столбец по наибольшему из положительных элементов целевой строки. Cs=max(Cj). Целевая строка выбирается по наилучшему значению отношения элемента последнего столбца к соответствующему элементу S-го столбца. Bi/ais=min (bk/aks), aks>0.

Б) На пересечении разрешающего столбца и разрешающей строки и находится разрешающий элемент. Ais>0

Когда разрешающий элемент ais производят симплексные преобразование матрицы:

1. Все элементы разрешающей строки делятся на разрешающий элемент.
2. Все элементы разрешающего столбца кроме разрешающего элемента заменяют 0.
3. Все остальные элементы матрицы заменяют по правилу прямоугольника.

Источник