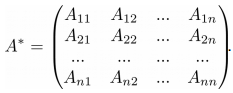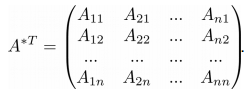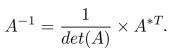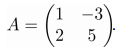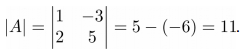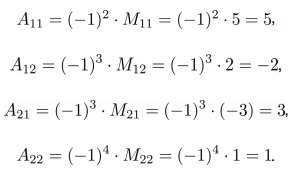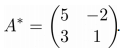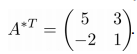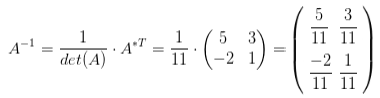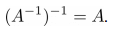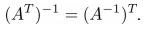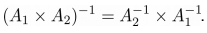Vorlogg / обратная матрица.py
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters
| a = [[ 7 , 2 , 0 ],[ 3 , 1 , 0 ],[ 1 , 1 , 1 ]] |
| b = [[ 0 , 2 , 3 ],[ 1 , 0 , — 2 ],[ 3 , 1 , 1 ]] |
| # !/usr/bin/python |
| # -*- coding: CP866 -*- |
| # Нахождение обратной матрицы, и Детерминанта, примеры на Python |
| import math # подключаем модуль математических функций |
| def determinant ( dim , data ): # функция вычисления детерминанты |
| if dim == 0 : |
| det = 0 |
| if dim == 1 : |
| det = data [ 0 ] |
| if dim == 2 : |
| det = data [ 0 ] * data [ 3 ] — data [ 2 ] * data [ 1 ] |
| if dim == 3 : |
| det = data [ 0 ] * data [ 4 ] * data [ 8 ] + data [ 1 ] * data [ 5 ] * data [ 6 ] + data [ 2 ] * data [ 3 ] * data [ 7 ] — data [ 6 ] * data [ |
| 4 ] * data [ 2 ] — data [ 7 ] * data [ 5 ] * data [ 0 ] — data [ 8 ] * data [ 3 ] * data [ 1 ] |
| if dim > 3 : |
| det = 0 |
| i = 0 |
| for j in range ( dim ): |
| det += data [ i * dim + j ] * cofactor ( dim , data , i , j ) |
| return det |
| def minor ( dim , data , i , j ): |
| new_matrix = [] |
| for k in range ( dim * dim ): |
| if ( math . floor ( k / dim ) != i and k % dim != j ): |
| new_matrix . append ( data [ k ]) |
| return determinant ( dim — 1 , new_matrix ) |
| def cofactor ( dim , data , i , j ): # функция вычисления кофактора |
| return math . pow ( — 1 , i + j ) * minor ( dim , data , i , j ) |
| def cofactor_matrix ( dim , data ): # функция вычисления кофакторной матрицы |
| new_matrix = [] |
| for i in range ( dim ): |
| for j in range ( dim ): |
| new_matrix . append ( cofactor ( dim , data , i , j )) |
| return new_matrix |
| def transpose_matrix ( dim , data ): #транспонирование |
| new_matrix = [] |
| for i in range ( dim ): |
| for j in range ( dim ): |
| new_matrix . append ( data [ j * dim + i ]) |
| return new_matrix |
| def adjoint_matrix ( dim , data ): #союзная матрица |
| return transpose_matrix ( dim , cofactor_matrix ( dim , data )) |
| matix = [[ 2 , 2 , 1 , 2 , 5 ], [ 1 , 3 , 3 , 1 , 3 ], [ 1 , 2 , 2 , 1 , 3 ], [ 4 , 2 , 2 , 3 , 8 ], [ 1 , 5 , 2 , 1 , 1 ]] # Пример матрицы |
| matix = a |
| data = [] # создаем пустую матрицу |
| for i in range ( len ( matix )): # создаем счетчик итераций на основе размера матрицы matix |
| for j in range ( len ( matix )): # создаем счетчик итераций на основе размера матрицы matix |
| data = data + [ matix [ i ][ j ]] # переводим квадратную матрицу matix в плоскую |
| dim = len ( matix ) # размер матрицы |
| dim2 = dim * dim # находим квадрат |
| det = determinant ( dim , data ) # находим детерминанту |
| print ( |
| ‘Детерминант: |A| =: ‘ , det # |
| ) |
| print () |
| print ( |
| ‘Обратная матрица : ‘ ) |
| print () |
| if det != 0 : # если матрица имеет детерминант не равный нулю |
| adj_matrix = adjoint_matrix ( dim , data ) # находим значение строк матрицы |
| for n in range ( dim2 ): # создаем счетчик итерации |
| cs = int (( adj_matrix [ n ]) / det ) # находим значение ячейки матрицы |
| if cs < 0 : # условие при котором значение меньше нуля |
| pr = » » # 3 пробела для форматирования |
| else : # иначе |
| pr = » » # 4 пробела для форматирования |
| g = pr + str ( cs ) + » » # конкатинация пробелов и значения ячейки матрицы |
| print ( |
| g ), # выводим значение переменной g |
| if ( n % dim == dim — 1 ): # |
| print () # пустая строка |
| else : # иначе |
| print ( |
| ‘Это вырожденная матрица, обратную матрицу найти невозможно’ ) # выводим сообщение о том что матрица вырождена |
Линейная алгебра на Python. [Урок 5]. Обратная матрица и ранг матрицы
Обратной матрицей A -1 матрицы A называют матрицу, удовлетворяющую следующему равенству:
где – E это единичная матрица.
Для того, чтобы у квадратной матрицы A была обратная матрица необходимо и достаточно чтобы определитель |A| был не равен нулю. Введем понятие союзной матрицы . Союзная матрица A* строится на базе исходной A путем замены всех элементов матрицы A на их алгебраические дополнения.
Транспонируя матрицу A*, мы получим так называемую присоединенную матрицу A* T :
Теперь, зная как вычислять определитель и присоединенную матрицу, мы можем определить матрицу A -1 , обратную матрице A:
Пример вычисления обратной матрицы. Пусть дана исходная матрица A, следующего вида:
Для начала найдем определитель матрицы A:
Как видно из приведенных вычислений, определитель матрицы не равен нулю, значит у матрицы A есть обратная. Построим присоединенную матрицу, для этого вычислим алгебраические дополнения для каждого элемента матрицы A:
Союзная матрица будет иметь следующий вид:
Присоединенная матрица получается из союзной путем транспонирования:
Решим задачу определения обратной матрицы на Python. Для получения обратной матрицы будем использовать функцию inv():
>>> A = np.matrix('1 -3; 2 5') >>> A_inv = np.linalg.inv(A) >>> print(A_inv) [[ 0.45454545 0.27272727] [-0.18181818 0.09090909]] Рассмотрим свойства обратной матрицы.
Свойство 1 . Обратная матрица обратной матрицы есть исходная матрица:
>>> A = np.matrix('1. -3.; 2. 5.') >>> A_inv = np.linalg.inv(A) >>> A_inv_inv = np.linalg.inv(A_inv) >>> print(A) [[1. -3.] [2. 5.]] >>> print(A_inv_inv) [[1. -3.] [2. 5.]] Свойство 2 . Обратная матрица транспонированной матрицы равна транспонированной матрице от обратной матрицы:
>>> A = np.matrix('1. -3.; 2. 5.') >>> L = np.linalg.inv(A.T) >>> R = (np.linalg.inv(A)).T >>> print(L) [[ 0.45454545 -0.18181818] [ 0.27272727 0.09090909]] >>> print(R) [[ 0.45454545 -0.18181818] [ 0.27272727 0.09090909]] Свойство 3 . Обратная матрица произведения матриц равна произведению обратных матриц:
>>> A = np.matrix('1. -3.; 2. 5.') >>> B = np.matrix('7. 6.; 1. 8.') >>> L = np.linalg.inv(A.dot(B)) >>> R = np.linalg.inv(B).dot(np.linalg.inv(A)) >>> print(L) [[ 0.09454545 0.03272727] [-0.03454545 0.00727273]] >>> print(R) [[ 0.09454545 0.03272727] [-0.03454545 0.00727273]] Ранг матрицы
Ранг матрицы является еще одной важной численной характеристикой. Рангом называют максимальное число линейно независимых строк (столбцов) матрицы. Линейная независимость означает, что строки (столбцы) не могут быть линейно выражены через другие строки (столбцы). Ранг матрицы можно найти через ее миноры, он равен наибольшему порядку минора, который не равен нулю. Существование ранга у матрицы не зависит от того квадратная она или нет.
Вычислим ранг матрицы с помощью Python. Создадим единичную матрицу:
>>> m_eye = np.eye(4) >>> print(m_eye) [[1. 0. 0. 0.] [0. 1. 0. 0.] [0. 0. 1. 0.] [0. 0. 0. 1.]]
Ранг такой матрицы равен количеству ее столбцов (или строк), в нашем случае ранг будет равен четырем, для его вычисления на Python воспользуемся функцией matrix_rank():
>>> rank = np.linalg.matrix_rank(m_eye) >>> print(rank) 4
Если мы приравняем элемент в нижнем правом углу к нулю, то ранг станет равен трем:
>>> m_eye[3][3] = 0 >>> print(m_eye) [[1. 0. 0. 0.] [0. 1. 0. 0.] [0. 0. 1. 0.] [0. 0. 0. 0.]] >>> rank = np.linalg.matrix_rank(m_eye) >>> print(rank) 3
P.S.
Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта . Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
Линейная алгебра на Python. [Урок 5]. Обратная матрица и ранг матрицы : 1 комментарий
- pedro kekulé 23.10.2019 i want that help me
1) написать программу вычисляющую обратную матрицу 2) написать программу для решения СЛАУ с помощью обратной матрицы 3) сравнить скорость работы всех трёх методов решения СЛАУ