scipy.stats.norm#
The location ( loc ) keyword specifies the mean. The scale ( scale ) keyword specifies the standard deviation.
As an instance of the rv_continuous class, norm object inherits from it a collection of generic methods (see below for the full list), and completes them with details specific for this particular distribution.
The probability density function for norm is:
The probability density above is defined in the “standardized” form. To shift and/or scale the distribution use the loc and scale parameters. Specifically, norm.pdf(x, loc, scale) is identically equivalent to norm.pdf(y) / scale with y = (x — loc) / scale . Note that shifting the location of a distribution does not make it a “noncentral” distribution; noncentral generalizations of some distributions are available in separate classes.
>>> import numpy as np >>> from scipy.stats import norm >>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots(1, 1)
Calculate the first four moments:
>>> mean, var, skew, kurt = norm.stats(moments='mvsk')
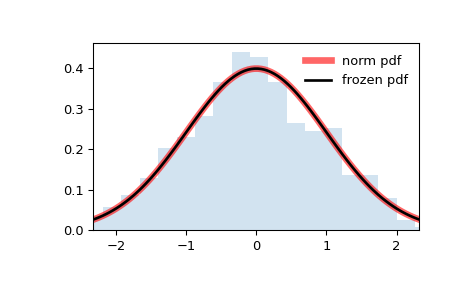
Display the probability density function ( pdf ):
>>> x = np.linspace(norm.ppf(0.01), . norm.ppf(0.99), 100) >>> ax.plot(x, norm.pdf(x), . 'r-', lw=5, alpha=0.6, label='norm pdf')
Alternatively, the distribution object can be called (as a function) to fix the shape, location and scale parameters. This returns a “frozen” RV object holding the given parameters fixed.
Freeze the distribution and display the frozen pdf :
>>> rv = norm() >>> ax.plot(x, rv.pdf(x), 'k-', lw=2, label='frozen pdf')
Check accuracy of cdf and ppf :
>>> vals = norm.ppf([0.001, 0.5, 0.999]) >>> np.allclose([0.001, 0.5, 0.999], norm.cdf(vals)) True
And compare the histogram:
>>> ax.hist(r, density=True, bins='auto', histtype='stepfilled', alpha=0.2) >>> ax.set_xlim([x[0], x[-1]]) >>> ax.legend(loc='best', frameon=False) >>> plt.show()
rvs(loc=0, scale=1, size=1, random_state=None)
pdf(x, loc=0, scale=1)
Probability density function.
logpdf(x, loc=0, scale=1)
Log of the probability density function.
cdf(x, loc=0, scale=1)
Cumulative distribution function.
logcdf(x, loc=0, scale=1)
Log of the cumulative distribution function.
sf(x, loc=0, scale=1)
Survival function (also defined as 1 — cdf , but sf is sometimes more accurate).
logsf(x, loc=0, scale=1)
Log of the survival function.
ppf(q, loc=0, scale=1)
Percent point function (inverse of cdf — percentiles).
isf(q, loc=0, scale=1)
Inverse survival function (inverse of sf ).
moment(order, loc=0, scale=1)
Non-central moment of the specified order.
stats(loc=0, scale=1, moments=’mv’)
Mean(‘m’), variance(‘v’), skew(‘s’), and/or kurtosis(‘k’).
entropy(loc=0, scale=1)
(Differential) entropy of the RV.
Parameter estimates for generic data. See scipy.stats.rv_continuous.fit for detailed documentation of the keyword arguments.
expect(func, args=(), loc=0, scale=1, lb=None, ub=None, conditional=False, **kwds)
Expected value of a function (of one argument) with respect to the distribution.
median(loc=0, scale=1)
Median of the distribution.
mean(loc=0, scale=1)
var(loc=0, scale=1)
Variance of the distribution.
std(loc=0, scale=1)
Standard deviation of the distribution.
interval(confidence, loc=0, scale=1)
Confidence interval with equal areas around the median.
Как рассчитать обратное значение нормальной кумулятивной функции распределения в Python?
Как вычислить обратную функцию кумулятивного распределения (CDF) нормального распределения в Python? Какую библиотеку я должен использовать? Возможно, скудный?
Вы имеете в виду обратное распределение Гаусса ( en.wikipedia.org/wiki/Inverse_Gaussian_distribution ) или обратное кумулятивной функции распределения нормального распределения ( en.wikipedia.org/wiki/Normal_distribution ) или что-то еще?
2 ответа
NORMSINV (упоминается в комментарии) является обратным к CDF стандартного нормального распределения. Используя scipy , вы можете вычислить это с помощью метода ppf объекта scipy.stats.norm . Аббревиатура ppf означает функция процентных точек, которая является другим именем функция квантильности.
In [20]: from scipy.stats import norm In [21]: norm.ppf(0.95) Out[21]: 1.6448536269514722 Убедитесь, что он является обратным для CDF:
In [34]: norm.cdf(norm.ppf(0.95)) Out[34]: 0.94999999999999996 По умолчанию norm.ppf использует среднее value = 0 и stddev = 1, что является стандартным нормальным распределением. Вы можете использовать другое среднее и стандартное отклонение, указав аргументы loc и scale , соответственно.
In [35]: norm.ppf(0.95, loc=10, scale=2) Out[35]: 13.289707253902945 Если вы посмотрите на исходный код для scipy.stats.norm , вы обнаружите, что метод ppf в конечном итоге вызывает scipy.special.ndtri . Таким образом, чтобы вычислить инверсию CDF стандартного нормального распределения, вы можете использовать эту функцию напрямую:
In [43]: from scipy.special import ndtri In [44]: ndtri(0.95) Out[44]: 1.6448536269514722 Я всегда думаю, что «функция процентной точки» (ppf) — ужасное имя. Большинство людей в статистике просто используют «квантильную функцию».
# given random variable X (house price) with population muy = 60, sigma = 40 import scipy as sc import scipy.stats as sct sc.version.full_version # 0.15.1 #a. Find P(X<50) sct.norm.cdf(x=50,loc=60,scale=40) # 0.4012936743170763 #b. Find P(X>=50) sct.norm.sf(x=50,loc=60,scale=40) # 0.5987063256829237 #c. Find P(60<=X<=80) sct.norm.cdf(x=80,loc=60,scale=40) - sct.norm.cdf(x=60,loc=60,scale=40) #d. how much top most 5% expensive house cost at least? or find x where P(X>=x) = 0.05 sct.norm.isf(q=0.05,loc=60,scale=40) #e. how much top most 5% cheapest house cost at least? or find x where P(X<=x) = 0.05 sct.norm.ppf(q=0.05,loc=60,scale=40) Ещё вопросы
- 0 как использовать q.all в Angular Js?
- 0 MySQL Выберите поле как Distinct с типом данных как Text с фильтрацией
- 1 Каково идеальное место для кэширования изображений?
- 0 Кеширование с JSP и HTML5: как отключить кеширование на стороне сервера
- 1 Springdata: mongodb находит запрос с необязательными «критериями»
- 0 о конструкторе копирования и перегруженном операторе присваивания
- 1 Ведение журнала TimedRotatingFileHandler не работает правильно
- 0 MySQL два внешних ключа из одной таблицы
- 1 заголовок столбца numpysavetxt
- 1 Понимание поведения тензорного потока при извлечении данных из двух разных источников данных с помощью набора данных API
- 0 Путь к изображению не работает в рамках YII?
- 1 Обработка файловых операций с сопрограммами
- 1 Конкретная строка данных в Pandas кажется индексной
- 1 NiFi: Какой процессор я бы использовал для подключения к стороннему API, требующему 3 учетных элемента?
- 0 Как закрыть другой аккордеон в угловых js
- 1 C # Проверка xml против нескольких схем xsd
- 0 Как перемещаться по пунктам / деталям в списке JqeuryMobile
- 0 Функция заголовка php перенаправляет только на локальные страницы
- 1 Как установить значок на значок приложения программно?
- 1 Android Constraint Layout alignemnt
- 1 Как отобразить сообщение только один раз, когда таймер достигает 15 секунд
- 0 Magento 1.9 изменить базовый образ с phpMyAdmin
- 0 Сортировать массив по указанным идентификаторам?
- 0 Сконфигурируйте пользовательский интерфейс Angularjs из Java перед загрузкой сетки
- 0 Как динамически изменить шаблон поповера в angular-strap
- 1 Не удается импортировать установленный пакет в среде Python3 ноутбука Jupyter
- 0 Android-браузер не распознает шрифт
- 1 Перестановки отфильтрованы без повторяющихся символов
- 0 TBB Linker error Как узнать, что я пропустил включение или код устарел?
- 0 Серверная обработка данных jquery в Zend Framework
- 1 «ggbApplet не определен» ошибка в JavaScript
- 0 Ошибка консоли ZF2 - Get не удалось получить или создать экземпляр для ViewRenderer
- 0 когда-нибудь MySQL отключен, из-за увеличения нагрузки посетителя
- 1 Как приостановить / возобновить видео в Exoplayer?
- 1 найти значение, соответствующее дате в пандах
- 0 Как применить Emojis к списку директив Angularjs?
- 0 PHP Curl Check 404: всегда возвращать HTTPCODE 200 OK
- 1 Angular CLI использует SystemJS?
- 0 Привести итератор к другому типу
- 1 Использование AWS шифрования SDK в Python AWS лямбда
- 0 Привязка к следующему элементу только при первой прокрутке
- 1 Python-запросы GET со строками из списка
- 1 Отправить письмо без аутентификации
- 1 Изменить значение вставки jsGrid на основе элемента управления select на странице
- 1 InvalidOperationException происходит при отмене токена
- 0 ограничение размера изображения лайтбокса
- 0 HTML несколько уровней развернуть свернуть для таблицы с большим количеством строк медленно
- 0 Ошибка преобразования скобок из инфикса в постфикс
- 1 Почему это значение возвращает ноль?
- 1 Как начать потоковое видео с помощью webRTC?
scipy.stats.f#
As an instance of the rv_continuous class, f object inherits from it a collection of generic methods (see below for the full list), and completes them with details specific for this particular distribution.
The probability density function for f is:
for \(x > 0\) and parameters \(df_1, df_2 > 0\) .
f takes dfn and dfd as shape parameters.
The probability density above is defined in the “standardized” form. To shift and/or scale the distribution use the loc and scale parameters. Specifically, f.pdf(x, dfn, dfd, loc, scale) is identically equivalent to f.pdf(y, dfn, dfd) / scale with y = (x - loc) / scale . Note that shifting the location of a distribution does not make it a “noncentral” distribution; noncentral generalizations of some distributions are available in separate classes.
>>> import numpy as np >>> from scipy.stats import f >>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots(1, 1)
Calculate the first four moments:
>>> dfn, dfd = 29, 18 >>> mean, var, skew, kurt = f.stats(dfn, dfd, moments='mvsk')
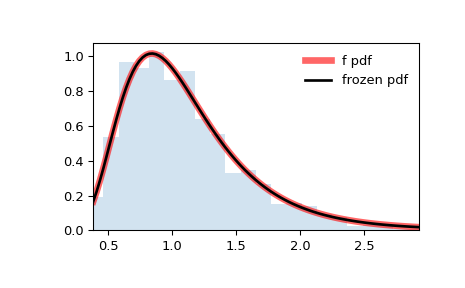
Display the probability density function ( pdf ):
>>> x = np.linspace(f.ppf(0.01, dfn, dfd), . f.ppf(0.99, dfn, dfd), 100) >>> ax.plot(x, f.pdf(x, dfn, dfd), . 'r-', lw=5, alpha=0.6, label='f pdf')
Alternatively, the distribution object can be called (as a function) to fix the shape, location and scale parameters. This returns a “frozen” RV object holding the given parameters fixed.
Freeze the distribution and display the frozen pdf :
>>> rv = f(dfn, dfd) >>> ax.plot(x, rv.pdf(x), 'k-', lw=2, label='frozen pdf')
Check accuracy of cdf and ppf :
>>> vals = f.ppf([0.001, 0.5, 0.999], dfn, dfd) >>> np.allclose([0.001, 0.5, 0.999], f.cdf(vals, dfn, dfd)) True
And compare the histogram:
>>> ax.hist(r, density=True, bins='auto', histtype='stepfilled', alpha=0.2) >>> ax.set_xlim([x[0], x[-1]]) >>> ax.legend(loc='best', frameon=False) >>> plt.show()
rvs(dfn, dfd, loc=0, scale=1, size=1, random_state=None)
pdf(x, dfn, dfd, loc=0, scale=1)
Probability density function.
logpdf(x, dfn, dfd, loc=0, scale=1)
Log of the probability density function.
cdf(x, dfn, dfd, loc=0, scale=1)
Cumulative distribution function.
logcdf(x, dfn, dfd, loc=0, scale=1)
Log of the cumulative distribution function.
sf(x, dfn, dfd, loc=0, scale=1)
Survival function (also defined as 1 - cdf , but sf is sometimes more accurate).
logsf(x, dfn, dfd, loc=0, scale=1)
Log of the survival function.
ppf(q, dfn, dfd, loc=0, scale=1)
Percent point function (inverse of cdf — percentiles).
isf(q, dfn, dfd, loc=0, scale=1)
Inverse survival function (inverse of sf ).
moment(order, dfn, dfd, loc=0, scale=1)
Non-central moment of the specified order.
stats(dfn, dfd, loc=0, scale=1, moments=’mv’)
Mean(‘m’), variance(‘v’), skew(‘s’), and/or kurtosis(‘k’).
entropy(dfn, dfd, loc=0, scale=1)
(Differential) entropy of the RV.
Parameter estimates for generic data. See scipy.stats.rv_continuous.fit for detailed documentation of the keyword arguments.
expect(func, args=(dfn, dfd), loc=0, scale=1, lb=None, ub=None, conditional=False, **kwds)
Expected value of a function (of one argument) with respect to the distribution.
median(dfn, dfd, loc=0, scale=1)
Median of the distribution.
mean(dfn, dfd, loc=0, scale=1)
var(dfn, dfd, loc=0, scale=1)
Variance of the distribution.
std(dfn, dfd, loc=0, scale=1)
Standard deviation of the distribution.
interval(confidence, dfn, dfd, loc=0, scale=1)
Confidence interval with equal areas around the median.