Нужна ли рекурсия в программировании

Что такое рекурсивное программирование: примеры, плюсы и минусы рекурсивных функций

Для решения некоторых задач рекурсия эффективнее циклов, однако она требует безошибочного кода и большего объема памяти. В противном случае возникнут ошибки или сбои во время выполнения функции. В этой статье вы узнаете о рекурсии, особенностях ее работы и увидите наглядные примеры.

Что такое рекурсия

Так называют поведение функции, когда она повторно вызывает саму себя. Рекурсия отличается от цикла тем, что не просто повторяется, а создает одну функцию внутри другой. Этот термин считается ключевым в программировании. Его можно сравнить с математической индукцией — функция выполнится после того, как получен ее результат при вызове с новыми данными.

Принцип работы рекурсии: функция А от двух запускает А от трех и т. д., пока не она достигнет завершающего условия. Они работают одновременно, а ответ выдается только после завершения последней вложенной функции и подсчета всех результатов.

Рекурсивный вызов поддерживается во всех распространенных языках программирования, включая Python, JavaScript, C. Он внедряется для решения задач, которые сложно или невозможно решить с помощью циклов.

• подобные решения чище и короче итерационных — вместо 40–50 строк программисту достаточно 5–10;
• подходит для выполнения крупных задач, т. к. разделяет их на части, что позволяет распараллелить задачи.

Резюмируя, рекурсивный процесс предполагает не поэтапную обработку, а деление чего-то большого на части до тех пор, пока решение не станет максимально простым.

Виды

Рекурсию подразделяют на 2 вида:

• прямая — функции вызывают сами себя, подставляя новые аргументы;
• косвенная — запуск происходит через сторонний блок кода, т. е. функция А вызывает Б, а последний снова А.

Последний вариант является менее очевидным и реже встречается. Его стоит использовать только при необходимости, т. к. такой код сложно воспринимать. Пример косвенного рекурсивного программирования:

• цикл — выполняется одно и то же действие, но много раз;
• рекурсия — функция, вызывающая саму себя с новыми аргументами.

1. Функция вызывает саму себя и приостанавливается.

2. Начинается выполнение “дочерней” и создается новый блок, который кладется поверх предыдущего. Повторение происходит вплоть до достижения останавливающего условия.

3. Функции начинают возвращать результат поэтапно и складывать их, т. е. первая выдает 1, а вторая — 2 + 1. После выполнения действия блок выходит из стека.

4. Программа выдает последний результат, полученный после завершения всех этапов.

• легко читаются — в коммерческом программировании над одним кодом работает целая команда, поэтому разработчики стараются максимально упростить его, чтобы коллеги смогли разобраться. Рекурсия получается короткой и емкой, благодаря чему проблемы с пониманием значения кода не возникнут;
• естественность — многие структуры данных и объектов ЯП рекурсивны по своей природе, например: фракталы, классовая иерархия, древовидные структуры;
• защита от ошибок — рекурсивные алгоритмы не сталкиваются с такими проблемами, как «действия выполнены в неверном порядке», «использована неинициализированная переменная».

• бесконечностью — эта частая проблема, когда не достигается базовый случай. Программа создает максимальное количество функций, зависает, а пользователь получает ошибку;
• переполнением стека — действия не выполняются, пока последний вызов не будет совершен. Из-за этого программа забирает много ресурсов, что может привести к падению производительности.

Алгоритм дифференцирует массив на 2 составляющие и выделяет 2 простых случая, которые не требуют дальнейшего упрощения, т. е. выполняется обработка всей совокупности или первая составляющая является искомой.

Пример реального кода на JavaScript:

function look_for_key(box) < for (item in box) < if (item.is_a_box()) < look_for_key(item); >else if (item.is_a_key()) < console.log("I found the key!") >> > 

Последний вариант проще, т. к. в нем нужно найти только объект в одной из коробок. Она отражает человеческую логику — раскладываешь коробки, в которых возможно находится ключ, и осматриваешь их.

Поиск факториала

Если вам нужно посчитать факториал, на языке программирования Java это делается следующим образом:

public class Solution < public static int recursion(int n) < if (n == 1) < // Это базовый случай return 1; >return recursion(n - 1) * n; // Рекурсивный шаг > public static void main(String[] args) < System.out.println(recursion(5)); // Вызов функции >> 

Палиндром

Так называют число, слово, текст, которые с разных сторон читаются одинаково, т. е. 101, топот или финское слово saippuakivikauppias. Пример определения палиндрома на Java:

public class Solution < public static String recursion(String s) < // Базовый случай if (s.length() == 1) < return "YES"; >else < if (s.substring(0, 1).equals(s.substring(s.length() - 1, s.length()))) < // Базовый случай if (s.length() == 2) < return "YES"; >// Шаг рекурсии return recursion(s.substring(1, s.length() - 1)); > else < return "NO"; >> > public static void main(String[] args) < System.out.println(recursion("radar")); // Вызов >> 

Что выбрать: рекурсию или цикл

Выбор средств зависит от поставленной задачи и требований, например:

• если необходима большая скорость выполнения и минимальная нагрузка, или существует опасность перегрузки памяти — выбирают циклы;
• когда важна читаемость и лаконичность кода — рекурсию.

Последний вариант выбирают в задачах, когда нужно, например, обойти вложенные каталоги. Обычно в них есть свои переменные, асинхронные потоки. Их легче обработать, используя рекурсию, т. к. результат обхода одного каталога не влияет на итоги анализа следующего.

Также рекурсия эффективна, если функция кэшируема, т. е. запоминает данные и на следующих этапах возвращается сохраненная информация.

Выводы

Таким образом, рекурсия — функция, вызывающая сама себя. Она содержит базовый случай и передает новым уровням измененные данные. Информация хранится в стеке, поэтому возможно переполнение с последующей остановкой программы. Рекурсивные алгоритмы обычно работают медленнее итерационных, однако легче пишутся и читаются.

Источник

Как работает рекурсия – объяснение в блок-схемах и видео

Представляю вашему вниманию перевод статьи Beau Carnes How Recursion Works — explained with flowcharts and a video.

Рекурсию порой сложно понять, особенно новичкам в программировании. Если говорить просто, то рекурсия – это функция, которая сама вызывает себя. Но давайте попробую объяснить на примере.

Представьте, что вы пытаетесь открыть дверь в спальню, а она закрыта. Ваш трехлетний сынок появляется из-за угла и говорит, что единственный ключ спрятан в коробке. Вы опаздываете на работу и Вам действительно нужно попасть в комнату и взять вашу рубашку.

Вы открываете коробку только чтобы найти… еще больше коробок. Коробки внутри коробок и вы не знаете, в какой из них Ваш ключ. Вам срочно нужна рубашка, так что вам надо придумать хороший алгоритм и найти ключ.

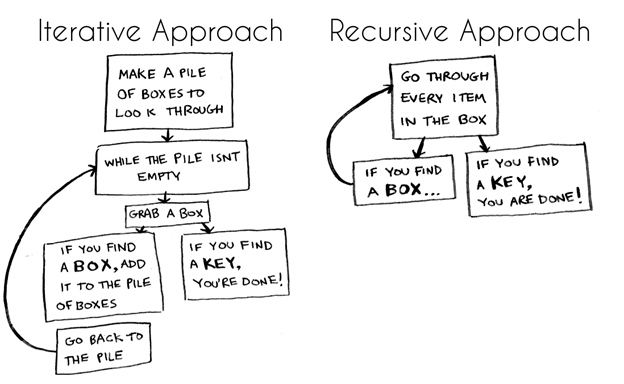
Есть два основных подхода в создании алгоритма для решения данной проблемы: итеративный и рекурсивный. Вот блок-схемы этих подходов:

Какой подход для Вас проще?

В первом подходе используется цикл while. Т.е. пока стопка коробок полная, хватай следующую коробку и смотри внутрь нее. Ниже немного псевдокода на Javascript, который отражает то, что происходит (Псевдокод написан как код, но больше похожий на человеческий язык).

function look_for_key(main_box) < let pile = main_box.make_a_pile_to_look_through(); while (pile is not empty) < box = pile.grab_a_box(); for (item in box) < if (item.is_a_box()) < pile.append(item) >else if (item.is_a_key()) < console.log("found the key!") >> > >

В другом подходе используется рекурсия. Помните, рекурсия – это когда функция вызывает саму себя. Вот второй вариант в псевдокоде:

function look_for_key(box) < for (item in box) < if (item.is_a_box()) < look_for_key(item); >else if (item.is_a_key()) < console.log("found the key!") >> >

Оба подхода выполняют одно и тоже. Основный смысл в использовании рекурсивного подхода в том, что однажды поняв, вы сможете легко его читать. В действительности нет никакого выигрыша в производительности от использования рекурсии. Порой итеративный подход с циклами будет работать быстрее, но простота рекурсии иногда предпочтительнее.

Поскольку рекурсия используется во многих алгоритмах, очень важно понять как она работает. Если рекурсия до сих пор не кажется Вам простой, не беспокойтесь: Я собираюсь пройтись еще по нескольким примерам.

Граничный и рекурсивный случай

То, что Вам необходимо принять во внимание при написании рекурсивной функции – это бесконечный цикл, т.е. когда функция вызывает саму себя… и никогда не может остановиться.
Допустим, Вы хотите написать функцию подсчета. Вы можете написать ее рекурсивно на Javascript, к примеру:

// WARNING: This function contains an infinite loop! function countdown(i) < console.log(i) countdown(i - 1) >countdown(5); // This is the initial call to the function.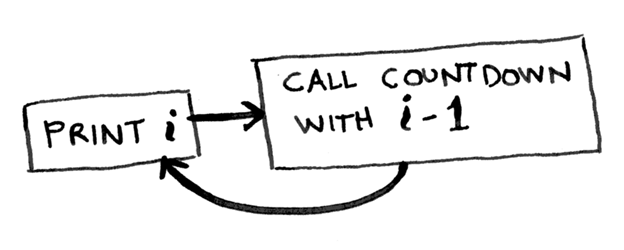

Эта функция будет считать до бесконечности. Так что, если Вы вдруг запустили код с бесконечным циклом, остановите его сочетанием клавиш «Ctrl-C». (Или, работая к примеру в CodePen, это можно сделать, добавив “?turn_off_js=true” в конце URL.)

Рекурсивная функция всегда должна знать, когда ей нужно остановиться. В рекурсивной функции всегда есть два случая: рекурсивный и граничный случаи. Рекурсивный случай – когда функция вызывает саму себя, а граничный – когда функция перестает себя вызывать. Наличие граничного случая и предотвращает зацикливание.

И снова функция подсчета, только уже с граничным случаем:

function countdown(i) < console.log(i) if (i else < // recursive case countdown(i - 1) >> countdown(5); // This is the initial call to the function.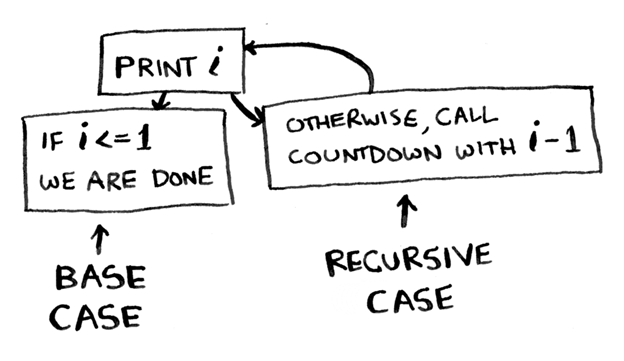

То, что происходит в этой функции может и не быть абсолютно очевидным. Я поясню, что произойдет, когда вы вызовете функцию и передадите в нее цифру 5.

Сначала мы выведем цифру 5, используя команду Console.Log. Т.к. 5 не меньше или равно 1, то мы перейдем в блок else. Здесь мы снова вызовем функцию и передадим в нее цифру 4 (т.к. 5 – 1 = 4).

Мы выведем цифру 4. И снова i не меньше или равно 1, так что мы переходим в блок else и передаем цифру 3. Это продолжается, пока i не станет равным 1. И когда это случится мы выведем в консоль 1 и i станет меньше или равно 1. Наконец мы зайдем в блок с ключевым словом return и выйдем из функции.

Стек вызовов

Рекурсивные функции используют так называемый «Стек вызовов». Когда программа вызывает функцию, функция отправляется на верх стека вызовов. Это похоже на стопку книг, вы добавляете одну вещь за одни раз. Затем, когда вы готовы снять что-то обратно, вы всегда снимаете верхний элемент.

Я продемонстрирую Вам стек вызовов в действии, используя функцию подсчета факториала. Factorial(5) пишется как 5! и рассчитывается как 5! = 5*4*3*2*1. Вот рекурсивная функция для подсчета факториала числа:

Теперь, давайте посмотрим что же происходит, когда вы вызываете fact(3). Ниже приведена иллюстрация в которой шаг за шагом показано, что происходит в стеке. Самая верхняя коробка в стеке говорит Вам, что вызывать функции fact, на которой вы остановились в данный момент:

Заметили, как каждое обращение к функции fact содержит свою собственную копию x. Это очень важное условие для работы рекурсии. Вы не можете получить доступ к другой копии функции от x.

Нашли уже ключ?

Давайте кратенько вернемся к первоначальному примеру поиска ключа в коробках. Помните, что первым был итеративный подход с использованием циклов? Согласно этому подходу Вы создаете стопку коробок для поиска, поэтому всегда знаете в каких коробках вы еще не искали.

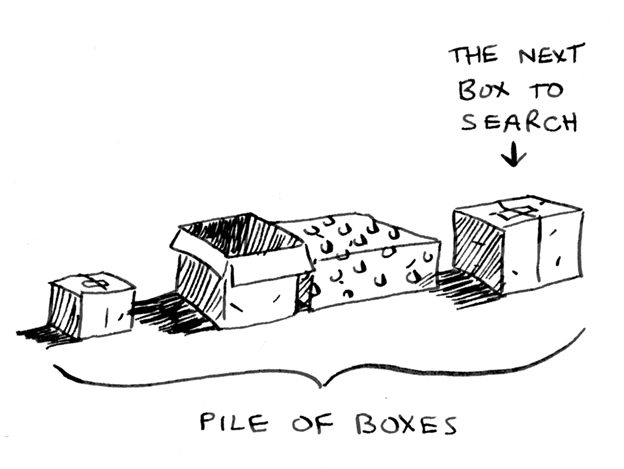
Но в рекурсивном подходе нет стопки. Так как тогда алгоритм понимает в какой коробке следует искать? Ответ: «Стопка коробок» сохраняется в стеке. Формируется стек из наполовину выполненных обращений к функции, каждое из которых содержит свой наполовину выполненный список из коробок для просмотра. Стек следит за стопкой коробок для Вас!

И так, спасибо рекурсии, Вы наконец смогли найти свой ключ и взять рубашку!

Вы также можете посмотреть мое пятиминутное видео про рекурсию. Оно должно усилить понимание, приведенных здесь концепций.

Заключение от автора

Надеюсь, что статья внесла немного больше ясности в Ваше понимание рекурсии в программировании. Основой для статьи послужил урок в моем новом видео курсе от Manning Publications под названием «Algorithms in Motion». И курс и статься написаны по замечательной книге «Grokking Algorithms», автором которой является Adit Bhargava, кем и были нарисованы все эти замечательные иллюстрации.

И наконец, чтобы действительно закрепить свои знания о рекурсии, Вы должны прочитать эту статью, как минимум, еще раз.

От себя хочу добавить, что с интересом наблюдаю за статьями и видеоуроками Beau Carnes, и надеюсь что Вам тоже понравилась статья и в особенности эти действительно замечательные иллюстрации из книги A. Bhargav «Grokking Algorithms».

Источник