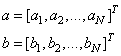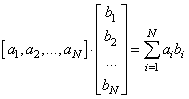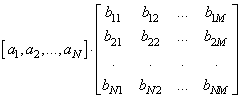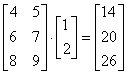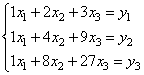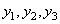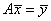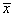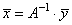Numpy python перемножить матрицы

Произведение матриц и векторов, элементы линейной алгебры

Пришло время познакомиться с одной из фундаментальных возможностей пакета NumPy–матричных и векторных вычислений. На одном из прошлых занятий мы с вами уже видели, как можно поэлементно умножать один вектор на другой или одну матрицу на другую:

a = np.arange(1, 10).reshape(3, 3) b = np.arange(10, 19).reshape(3, 3) a*b

В консоли увидим результат:

array([[ 10, 22, 36],
[ 52, 70, 90],
[112, 136, 162]])

Матричное умножение

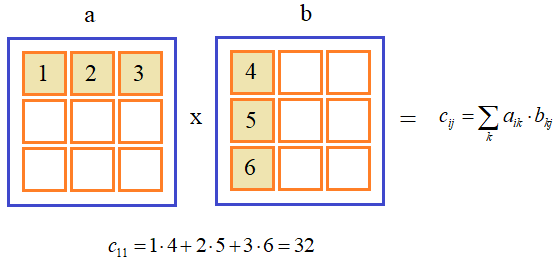
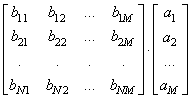
Но если нам нужно выполнить именно матричное умножение, то есть, строки одной матрицы умножать на столбцы другой и результаты складывать:

то для этого следует использовать специальные функции и операторы. Начнем с функций. Итак, чтобы перемножить две матрицы a иbпо всем правилам математики, запишем следующую команду:

Эта функция возвращает новую матрицу (двумерный массив) с результатом умножения:

array([[ 84, 90, 96],
[201, 216, 231],
[318, 342, 366]])

Тот же результат можно получить и с помощью функции:

Считается, что этот вариант предпочтительнее использовать при умножении матриц.

Векторное умножение

Аналогичные операции можно выполнять и с векторами. Математически, если у нас имеются два вектора:

то их умножение можно реализовать в двух видах:

Первое умножение реализуется либо через функцию:

a = np.arange(1, 10) b = np.ones(9) np.dot(a, b) # значение 45

Либо, более предпочтительной функцией для внутреннего умножения векторов:

Второй вариант умножения (внешнее умножение векторов) реализуется с помощью функции:

получим результат в виде следующей матрицы:

array([[1., 1., 1., 1., 1., 1., 1., 1., 1.],
[2., 2., 2., 2., 2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4., 4., 4., 4., 4.],
[5., 5., 5., 5., 5., 5., 5., 5., 5.],
[6., 6., 6., 6., 6., 6., 6., 6., 6.],
[7., 7., 7., 7., 7., 7., 7., 7., 7.],
[8., 8., 8., 8., 8., 8., 8., 8., 8.],
[9., 9., 9., 9., 9., 9., 9., 9., 9.]])

Операция умножения матриц и векторов используется довольно часто, поэтому в пакете NumPy имеется весьма полезный перегруженный оператор, заменяющий функцию matmul:

или, с использованием матриц:

a.resize(3, 3) b.resize(3, 3) a @ b # аналог np.matmul(a, b)

Умножение вектора на матрицу

Наконец, рассмотрим умножение вектора на матрицу. Это также можно записать двумя способами:

Для реализации первого способа, зададим одномерный вектор и двумерную матрицу:

a = np.array([1,2,3]) b = np.arange(4,10).reshape(3,2) # матрица 3x2

И, затем, воспользуемся уже знакомой нам функцией dot:

При такой записи, когда одномерный массив записан первым аргументом, а матрица – вторым, получаем умножение вектора-строки на матрицу, то есть, первый способ.

Для реализации второго способа аргументы нужно поменять местами: сначала указать матрицу, а затем, вектор. Но, если мы сейчас это сделаем с нашими массивами, то получим ошибку:

np.dot(b, a) # несогласованность размеров

Дело в том, что массив a должен представлять вектор длиной два элемента, так как матрица b имеет размер в 3 строки и 2 столбца:

Определим массивa в два элемента и умножим на матрицу b:

a = np.array([1, 2]) np.dot(b, a) # array([14, 20, 26])

Получаем вектор-строку (одномерный массив) как результат умножения. Обратите внимание, по правилам математики вектор aдолжен быть вектором-столбцом, то есть, быть представленным в виде:

a.shape = -1, 1 # вектор-столбец 2x1

Но мы использовали вектор-строку. В NumPyтак тоже можно делать и это не приведет к ошибке. Результат будет именно умножение матрицы как бы на вектор-столбец. Ну а если использовать вектор-столбец, то и на выходе получим вектор-столбец:

np.dot(b, a) # вектор-столбец 3x1

Этого же результат можно достичь, используя оператор @ (перегрузка функции matmul):

Результат будет тем же. Вот так в NumPyвыполняется умножение матриц, векторов и вектора на матрицу.

Элементы линейной алгебры

Из высшей математики хорошо известно, что матрицы можно использовать для решения систем линейных уравнений. Для этого в NumPyсуществует модуль linalg. Давайте рассмотрим некоторые из его функций.

Предположим, имеется квадратная матрица 3×3:

a = np.array([(1, 2, 3), (1, 4, 9), (1, 8, 27)])

Первым делом вычислим ранг этой матрицы, чтобы быть уверенным, что она состоит из линейно независимых строк и столбцов:

np.linalg.matrix_rank(a) # рангравен 3

Если ранг матрицы совпадает с ее размерностью, значит, она способна описывать систему из трех независимых линейных уравнений. В нашем случае, система уравнений будет иметь вид:

Здесь — некие числа линейного уравнения. Например, возьмем их равными:

Тогда корни уравнения можно вычислить с помощью функции solve:

np.linalg.solve(a, y) # array([-5. , 10. , -1.66666667])

Другой способ решения этой же системы линейных уравнений возможен через вычисление обратной матрицы. Изначально, уравнение можно записать в векторно-матричном виде:

Откуда получаем решения :

На уровне пакета NumPy это делается так:

invA = np.linalg.inv(a) # вычисление обратной матрицы invA @ y # вычисление корней

Источник

numpy.matmul#

A location into which the result is stored. If provided, it must have a shape that matches the signature (n,k),(k,m)->(n,m). If not provided or None, a freshly-allocated array is returned.

For other keyword-only arguments, see the ufunc docs .

New in version 1.16: Now handles ufunc kwargs

The matrix product of the inputs. This is a scalar only when both x1, x2 are 1-d vectors.

If the last dimension of x1 is not the same size as the second-to-last dimension of x2.

If a scalar value is passed in.

Complex-conjugating dot product.

Sum products over arbitrary axes.

Einstein summation convention.

alternative matrix product with different broadcasting rules.

The behavior depends on the arguments in the following way.

• If both arguments are 2-D they are multiplied like conventional matrices.
• If either argument is N-D, N > 2, it is treated as a stack of matrices residing in the last two indexes and broadcast accordingly.
• If the first argument is 1-D, it is promoted to a matrix by prepending a 1 to its dimensions. After matrix multiplication the prepended 1 is removed.
• If the second argument is 1-D, it is promoted to a matrix by appending a 1 to its dimensions. After matrix multiplication the appended 1 is removed.

matmul differs from dot in two important ways:

• Multiplication by scalars is not allowed, use * instead.
• Stacks of matrices are broadcast together as if the matrices were elements, respecting the signature (n,k),(k,m)->(n,m) :

>>> a = np.ones([9, 5, 7, 4]) >>> c = np.ones([9, 5, 4, 3]) >>> np.dot(a, c).shape (9, 5, 7, 9, 5, 3) >>> np.matmul(a, c).shape (9, 5, 7, 3) >>> # n is 7, k is 4, m is 3 

The matmul function implements the semantics of the @ operator introduced in Python 3.5 following PEP 465.

It uses an optimized BLAS library when possible (see numpy.linalg ).

For 2-D arrays it is the matrix product:

>>> a = np.array([[1, 0], . [0, 1]]) >>> b = np.array([[4, 1], . [2, 2]]) >>> np.matmul(a, b) array([[4, 1], [2, 2]]) 

For 2-D mixed with 1-D, the result is the usual.

>>> a = np.array([[1, 0], . [0, 1]]) >>> b = np.array([1, 2]) >>> np.matmul(a, b) array([1, 2]) >>> np.matmul(b, a) array([1, 2]) 

Broadcasting is conventional for stacks of arrays

>>> a = np.arange(2 * 2 * 4).reshape((2, 2, 4)) >>> b = np.arange(2 * 2 * 4).reshape((2, 4, 2)) >>> np.matmul(a,b).shape (2, 2, 2) >>> np.matmul(a, b)[0, 1, 1] 98 >>> sum(a[0, 1, :] * b[0 , :, 1]) 98 

Vector, vector returns the scalar inner product, but neither argument is complex-conjugated:

Scalar multiplication raises an error.

>>> np.matmul([1,2], 3) Traceback (most recent call last): . ValueError: matmul: Input operand 1 does not have enough dimensions . 

The @ operator can be used as a shorthand for np.matmul on ndarrays.

>>> x1 = np.array([2j, 3j]) >>> x2 = np.array([2j, 3j]) >>> x1 @ x2 (-13+0j) 

Источник

Базовые операции NumPy / np 3

Вы уже знаете, как создавать массив NumPy и как определять его элементы. Теперь пришло время разобраться с тем, как применять к ним различные операции.

Арифметические операторы

Арифметические операторы — первые, которые предстоит использовать. К числу наиболее очевидных относятся прибавление и умножение на скаляр.

>>> a = np.arange(4) >>> a array([0, 1, 2, 3]) >>> a+4 array([4, 5, 6, 7]) >>> a*2 array([0, 2, 4, 6]) 

Их можно использовать для двух массивов. В NumPy эти операции поэлементные, то есть, они применяются только к соответствующим друг другу элементам. Это должны быть объекты, которые занимают одно и то же положение, так что результатом станет новый массив, содержащий итоговые величины в тех же местах, что и операнды.

>>> b = np.arange(4,8) >>> b array([4, 5, 6, 7]) >>> a + b array([ 4, 6, 8, 10]) >>> a – b array([–4, –4, –4, –4]) >>> a * b array([ 0, 5, 12, 21]) 

Более того, эти операторы доступны и для функций, если те возвращают массив NumPy. Например, можно перемножить массив на синус или квадратный корень элементов массива b .

>>> a * np.sin(b) array([–0. , –0.95892427, –0.558831 , 1.9709598 ]) >>> a * np.sqrt(b) array([ 0. , 2.23606798, 4.89897949, 7.93725393]) 

И даже в случае с многомерными массивами можно применять арифметические операторы поэлементно.

>>> A = np.arange(0, 9).reshape(3, 3) >>> A array([[0, 1, 2], [3, 4, 5], [6, 7, 8]]) >>> B = np.ones((3, 3)) >>> B array([[ 1., 1., 1.], [ 1., 1., 1.], [ 1., 1., 1.]]) >>> A * B array([[ 0., 1., 2.], [ 3., 4., 5.], [ 6., 7., 8.]]) 

Произведение матриц

Выбор оператора для поэлементного применения — это странный аспект работы с библиотекой NumPy. В большинстве инструментов для анализа данных оператор * обозначает произведение матриц. Он применяется к обоим массивам. В NumPy же подобное произведение обозначается функцией dot() . Эта операция не поэлементная.

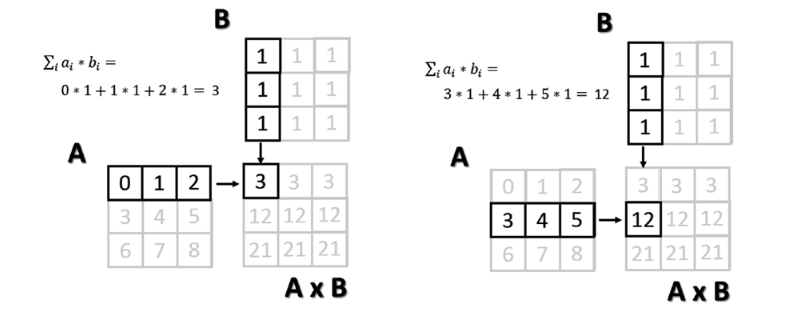
>>> np.dot(A,B) array([[ 3., 3., 3.], [ 12., 12., 12.], [ 21., 21., 21.]]) 

Каждый элемент результирующей матрицы — сумма произведений каждого элемента соответствующей строки в первой матрице с соответствующим элементом из колонки второй. Рисунок ниже показывает процесс произведения матриц (для двух элементов).

Еще один вариант записи произведения матриц — использование одной из двух матриц в качестве объекта функции dot() .

>>> A.dot(B) array([[ 3., 3., 3.], [ 12., 12., 12.], [ 21., 21., 21.]]) 

Но поскольку произведение матриц — это не коммутативная операция, порядок операндов имеет значение. В данном случае A*B не равняется B*A.

>>> np.dot(B,A) array([[ 9., 12., 15.], [ 9., 12., 15.], [ 9., 12., 15.]]) 

Операторы инкремента и декремента

На самом деле, в Python таких операторов нет, поскольку нет операторов ++ или — . Для увеличения или уменьшения значения используются += и -= . Они не отличаются от предыдущих, но вместо создания нового массива с результатами присваивают новое значение тому же массиву.

>>> a = np.arange(4) >>> a array([0, 1, 2, 3]) >>> a += 1 >>> a array([1, 2, 3, 4]) >>> a –= 1 >>> a array([0, 1, 2, 3]) 

Таким образом использование этих операторов дает возможность получать более масштабные результаты, чем в случае с обычными операторами инкремента, увеличивающими значения на один. Их можно использовать в самых разных ситуациях. Например, они подходят для изменения значений без создания нового массива.

array([0, 1, 2, 3]) >>> a += 4 >>> a array([4, 5, 6, 7]) >>> a *= 2 >>> a array([ 8, 10, 12, 14]) 

Универсальные функции (ufunc)

Универсальная функция, известная также как ufunc , — это функция, которая применяется в массиве к каждому элементу. Это значит, что она воздействует на каждый элемент массива ввода, генерируя соответствующий результат в массив вывода. Финальный массив соответствует по размеру массиву ввода.

Под это определение подпадает множество математических и тригонометрических операций; например, вычисление квадратного корня с помощью sqrt() , логарифма с log() или синуса с sin() .

>>> a = np.arange(1, 5) >>> a array([1, 2, 3, 4]) >>> np.sqrt(a) array([ 1. , 1.41421356, 1.73205081, 2. ]) >>> np.log(a) array([ 0. , 0.69314718, 1.09861229, 1.38629436]) >>> np.sin(a) array([ 0.84147098, 0.90929743, 0.14112001, –0.7568025 ]) 

Многие функции уже реализованы в библиотеке NumPy.

Функции агрегации

Функции агрегации выполняют операцию на наборе значений, например, на массиве, и выдают один результат. Таким образом, сумма всех элементов массива — это результат работы функции агрегации. Многие из таких функций реализованы в классе ndarray .

>>> a = np.array([3.3, 4.5, 1.2, 5.7, 0.3]) >>> a.sum() 15.0 >>> a.min() 0.29999999999999999 >>> a.max() 5.7000000000000002 >>> a.mean() 3.0 >>> a.std() 2.0079840636817816 

Источник