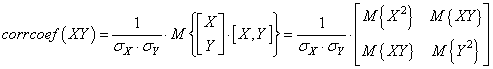Базовые математические функции
На этом занятии рассмотрим основные математические функции пакета NumPy, увидим, как они используются совместно с массивами.
Функции sum, mean, min и max
Итак, очень часто на практике требуется вычислять сумму значений элементов массива, их среднее значение, а также находить минимальные и максимальные значения. Для этих целей в NumPy существуют встроенные функции, выполняющие эти действия и сейчас мы посмотрим как они работают. Пусть, как всегда, у нас имеется одномерный массив:
a = np.array([ 1, 2, 3, 10, 20, 30])
Вычислим сумму, среднее значение и найдем максимальное и минимальное значения:
a.sum() # 66 a.mean() # 11.0 a.max() # 30 a.min() # 1
Как видите, все достаточно просто. Тот же самый результат будет получен и при использовании многомерных массивов. Например:
Но, если требуется вычислить сумму только по какой-то одной оси, то ее можно явно указать дополнительным параметром:
a.sum(axis=0) # array([24, 42]) a.sum(axis=1) # array([ 3, 13, 50])
Точно также работают и остальные три функции, например:
a.max(axis=0) # array([20, 30]) a.min(axis=1) # array([ 1, 3, 20])
Базовые математические функции
Предположим, имеется массив:
тогда для вычисления модулей значений его элементов можно записать команду:
np.abs(a) # array([ 1, 1, 5, 44, 32, 2])
На выходе получаем новый массив с абсолютными величинами. То же самое будет, если на вход подать обычный список значений:
np.abs([-1, 1, 5, -44, 32, ])# array([ 1, 1, 5, 44, 32])
Эти примеры демонстрируют разные типы входных данных: массив, список, число. Все это допустимо использовать в математических функциях.
Остальные функции работают по аналогии, например:
np.amax(a) # 32 np.log(a) # array([nan, 0. , 1.60943791, nan, 3.4657359,0.69314718]) np.around(0.7) # 1.0
Функции amin, amax, mean, argmax, argmin, при работе с многомерными матрицами, могут делать вычисления по строго определенной оси. Например:
a.resize(2, 3) np.amax(a, axis=0) # array([-1, 32, 5]) np.argmax(a, axis=1) # array([2, 1], dtype=int32)
Тригонометрические функции
Их использование также вполне очевидно. На входе они могут принимать массив, список или число. Если это угол, то он представляется в радианах. Например:
a = np.linspace(0, np.pi, 10) res1 = np.sin(a) # возвращает массив синусов углов np.sin(np.pi/3) np.cos([0, 1.57, 3.17]) res2 = np.cos(a) # возвращает массив косинусов углов np.arcsin(res1) # возвращает арксинусы от значений res1
Причем, все эти функции работают быстрее аналогичных функций языка Python. Поэтому, при использовании библиотеки NumPy предпочтение лучше отдавать именно ей, а не языку Python при тригонометрических вычислениях.
Функции генерации псевдослучайных чисел
Во многих программах требуется генерировать случайные значения и в NumPy для этого имеется специальный модуль random с богатым функционалом. Конечно, совершенно случайные величины получить невозможно, поэтому придумываются различные «хитрости» для их генерации и правильнее их называть – псевдослучанйыми числами.
В самом простом случае, функция rand() позволяет получать случайные числа в диапазоне от 0 до 1:
np.random.rand() # вещественное случайное число от 0 до 1
Если требуется получить массив из таких чисел, то можно указать это через первый аргумент:
np.random.rand(5) # array([0.78191696, 0.66581136, 0.46458873, 0.76416839, 0.28206656])
Для получения двумерных массивов – два аргумента:
np.random.rand(2, 3) # массив 2x3
И так далее. Можно создавать любые многомерные массивы из случайных величин.
Если требуется генерировать целые случайные значения, то используется функция randint():
np.random.randint(10) # генерация целых чисел в диапазоне [0; 10) np.random.randint(5, 10)# генерация в диапазоне [5; 10)
Для получения массива из таких случайных чисел дополнительно следует указать параметр size, следующим образом:
np.random.randint(5, size=4) # array([3, 1, 1, 4]) np.random.randint(1, 10, size=(2, 5)) # матрица 2x5
Функции rand() и randint() генерируют числа с равномерным законом распределения. Если нужно получать значения с другими широко известными распределениями, то используются функции:
np.random.randn() # нормальная СВ с нулевым средним и единичной дисперсией np.random.randn(5) # массив из пяти нормальных СВ np.random.randn(2, 3) # матрица 2x3 из нормальных СВ np.random.pareto(2.0, size=3) # распределение Паретто с параметром 2,0 np.random.beta(0.1, 0.3, size=(3, 3)) # бета-распределение с параметрами 0,1 и 0,3
Существуют и другие функции для генерации самых разных распределений. Документацию по ним можно посмотреть на официальном сайте пакета NumPy:
По умолчанию, все рассмотренные функции при каждом новом запуске генерируют разные числа. Однако, иногда требуются одни и те же их реализации. Например, такой подход часто используется для сохранения начальных случайных значений весов в нейронных сетях. Для этого устанавливают некое начальное значение зерна (seed):
np.random.seed(13) # начальное значение генератора случайных чисел
и все последующие запуски будут давать одну и ту же последовательность чисел, например:
np.random.randint(10, size=10) # array([2, 0, 0, 6, 2, 4, 9, 3, 4, 2])
Причем, у вас должны получиться такие же числа. Если запустим эту функцию еще раз, то будут получены следующие 10 случайных чисел:
np.random.randint(10, size=10) # array([6, 5, 9, 4, 2, 0, 3, 5, 3, 6])
Но, установив зерно снова в значение, например, 13:
np.random.randint(10, size=10) # array([2, 0, 0, 6, 2, 4, 9, 3, 4, 2]) np.random.randint(10, size=10) # array([6, 5, 9, 4, 2, 0, 3, 5, 3, 6])
Функции перемешивания элементов массива
np.random.shuffle() и np.random.permutation()
перемешивают случайным образом элементы массива. Например, дан массив:
a = np.arange(10) # array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
И нам требуется перетасовать его элементы. В самом простом случае, это делается так:
np.random.shuffle(a) # array([8, 7, 9, 6, 3, 4, 0, 2, 1, 5])
Причем, здесь меняется сам массив a. Если вызвать эту функцию еще раз:
np.random.shuffle(a) # array([7, 2, 1, 5, 8, 6, 4, 3, 9, 0])
то значения еще раз перетасуются. Но, работает она только с первой осью axis0. Например, если взять двумерный массив:
a = np.arange(1, 10).reshape(3, 3)
то в массиве aбудут переставлены только строки:
Вторая функция возвращает случайную последовательность чисел, генерируя последовательность «на лету»:
np.random.permutation(10) # array([8, 2, 7, 1, 0, 5, 3, 9, 4, 6])
Функции математической статистики
Рассмотрим работу этих функций. Предположим, имеются следующие векторы:
x = np.array([1, 4, 3, 7, 10, 8, 14, 21, 20, 23]) y = np.array([4, 1, 6, 9, 13, 11, 16, 19, 15, 22])
Эти числа будем воспринимать как реализации случайных величин X и Y. Тогда, для вычисления медианы СВX, можно воспользоваться функцией:
Для расчета дисперсии и СКО, функциями:
np.var(x) # дисперсия СВX на основе реализации x np.std(y) # СКО СВY на основе реализации y
Далее, чтобы рассчитать коэффициент корреляции Пирсона, объединим массивыx и y построчно:
XY = np.vstack([x, y]) # матрица 2x10
Результатом будет матрица 2×2:
array([[1. , 0.93158099],
[0.93158099, 1. ]])
Как ее следует интерпретировать? В действительности, это автоковариационная матрица вектора СВ[X, Y]:
(В этой формуле полагается, что СВX и Y центрированы, то есть имеют нулевое математическое ожидание).
Если нужно вычислить не нормированное МО, то есть, автоковариационную матрицу, то следует воспользоваться функцией:
np.cov(XY) # ковариационная матрица размерностью 2x2
Наконец, для вычисления взаимной корреляции между двумя векторамиx и y, используется функция:
np.correlate(x, y) # array([1736])
Более детальную информацию по этим статистическим функциям можно найти в официальной документации пакета NumPy:
Конечно, мы рассмотрели далеко не все математические функции NumPy. На следующем занятии продолжим эту тему и поговорим об умножении векторов и матриц, линейной алгебре и множествах.
Видео по теме
#1. Пакет numpy — установка и первое знакомство | NumPy уроки
#2. Основные типы данных. Создание массивов функцией array() | NumPy уроки
#3. Функции автозаполнения, создания матриц и числовых диапазонов | NumPy уроки
#4. Свойства и представления массивов, создание их копий | NumPy уроки
#5. Изменение формы массивов, добавление и удаление осей | NumPy уроки
#6. Объединение и разделение массивов | NumPy уроки
#7. Индексация, срезы, итерирование массивов | NumPy уроки
#8. Базовые математические операции над массивами | NumPy уроки
#9. Булевы операции и функции, значения inf и nan | NumPy уроки
#10. Базовые математические функции | NumPy уроки
#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy уроки
#12. Множества (unique) и операции над ними | NumPy уроки
#13. Транслирование массивов | NumPy уроки
© 2023 Частичное или полное копирование информации с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все тексты и изображения являются собственностью сайта