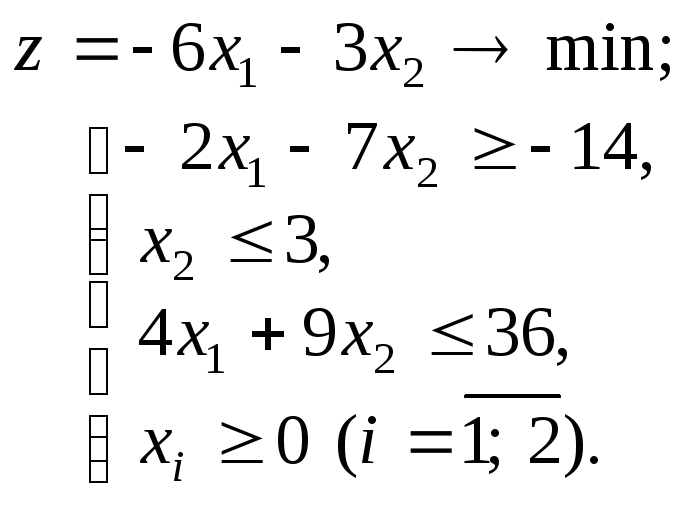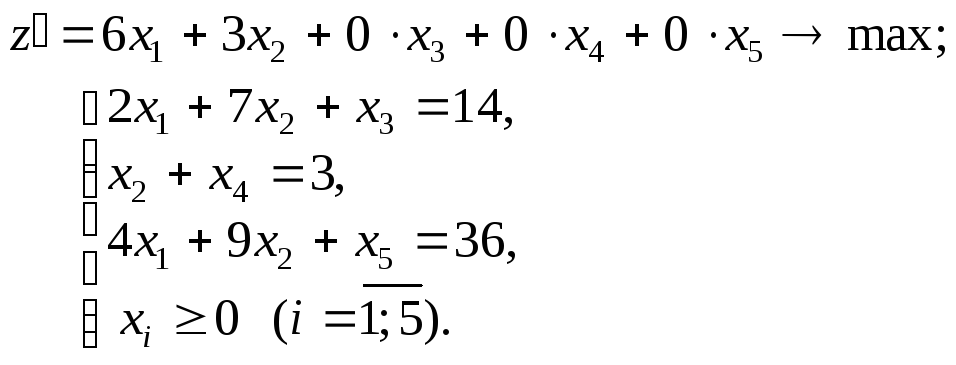Неограниченность целевой функции задачи линейного программирования

2.6. Контроль вычислений

Для контроля вычислений элементов индексной строки применяются формулы ₀=c_Б А₀,_j=с_б А_j –c_j.

2.7. Альтернативный оптимум (признак бесконечности множества оптимальных планов)

Теорема 3. Если в индексной строке последней симплексной таблицы, содержащей оптимальный план, имеется хотя бы одна нулевая оценка, соответствующая свободной переменной, то ЗЛП имеетбесконечное множество оптимальных планов.

Следствие. Если в индексной строке симплексной таблицы, содержащей оптимальный план, все оценки свободных переменных положительны, то найденныйоптимальный план единственный.

2.8. Признак неограниченности целевой функции

Теорема 4. Если в индексной строке симплексной таблицы ЗЛП на максимум (минимум) содержится отрицательная (положительная) оценка , а в соответствующем столбце переменной нет ни одного положительного элемента, то целевая функция на множестве допустимых планов задачи не ограничена сверху (снизу).Задача неразрешима.

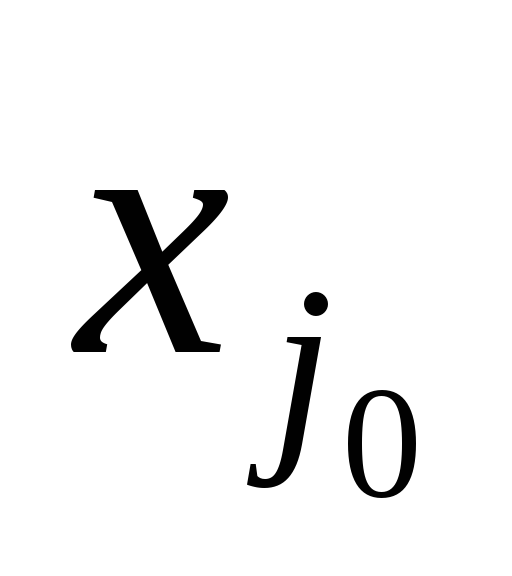
С экономической точки зрения неограниченность целевой функции ЗЛП свидетельствует только об одном: разработанная модель недостаточно точна.

Пример 2. Решить симплексным методом задачу

Упорядочим запись исходной задачи. Так как в первом неравенстве системы ограничений свободный член отрицателен, то умножим первое неравенство на –1. В результате получим

Ограничения-неравенства имеют вид , следовательно, целевая функция должна быть на максимум. В нашем случае задачу на минимум можно заменить задачей максимизации. Умножив целевую функцию на –1, получаем

Итак, запишем задачу в каноническом виде. Для этого добавим к левым частям неравенств дополнительные переменные x₃,x₄,x₅. В целевую функцию они сводятся с коэффициентами, равными нулю:

Задача имеет предпочтительный вид.

Переменные x₃,x₄,x₅– базисные, аx₁,x₂– свободные. Положим, чтоx₁=x₂= 0, тогдаx₃= 14,x₄= 3,x₅= 36. Следовательно,x₀= (0; 0; 14; 3; 36) является начальным опорным планом.

При этом 60 + 30 + 014 + 03 + 036 = 0. Заносим условие задачи в симплексную табл. 2.

Источник

6.2.4. Признак неограниченности целевой функции

Как следует из геометрической интерпретации ЗЛП, возможны случаи, когда функция цели Z при решении задачи на минимум не ограничена снизу. Этот случай легко выявить при решении задачи симплекс-методом.

Пусть среди компонент вектора в симплекс-таблице, соответствующей какому-либо опорному плану, имеется хотя бы одна отрицательная компонента, например , и при этом все коэффициенты s-столбца Покажем, что в этом случае ЗЛП не имеет решения вследствие неограниченности функции цели Z.

Пусть система ограничений ЗЛП приведена к базисному виду:

а целевая функция будет выражена через свободные переменные следующим образом:

Положив значения всех свободных переменных, кроме , равными нулю, будем иметь:

Так как то, вводя в базис переменную , можно уменьшить значение целевой функции.

Очевидно, что этой переменной можно придавать сколько угодно большие значения, при этом а значения всех остальных переменных остаются неотрицательными. Действительно:

Таким образом, ни одна из переменных не выйдет из базиса (не будет равна нулю).

А это означает, что, увеличивая , мы никогда не получим опорного решения, хотя значение функции при этом будет уменьшаться. Следовательно, задача не имеет решения вследствие неограниченности снизу целевой функции Z.

Вывод. Признаком неограниченности снизу функции Z в области допустимых решений является наличие хотя бы одного столбца неположительных коэффициентов системы ограничений, соответствующего компонентам исследуемого опорного плана в симплекс-таблице.

6.3. Понятие о вырождении

Опорное решение, в котором хотя бы одна из базисных переменных принимает нулевое значение, называется вырожденным, и соответствующая ЗЛП называется вырожденной.

Пусть, например, в вырожденном плане базисная переменная . Если на очередном шаге строка i0 окажется разрешающей, то и новое опорное решение также будет вырожденным (вводимая в базис в новом опорном плане переменная также будет равна нулю). Нетрудно видеть, что при этом значения всех остальных переменных остаются прежними, и значение целевой функции также не изменится. (Показать самим!)

Отсюда можно сделать вывод, что данная итерация не привела ни к каким изменениям и, следовательно, является лишней. Однако это не так. Изменяется состав базисных и свободных переменных. Вообще говоря, после конечного числа шагов можно вернуться к ранее встречавшемуся набору свободных и базисных переменных при неизменности значения целевой функции. Появляется так называемое зацикливание в схеме расчетов. Зацикливание недопустимо особенно при автоматизации процесса вычислений, так как требует вмешательства человека для изменения вычислительного алгоритма.

Поэтому существуют специальные методы избавления от зацикливания. Хотя вырожденные ЗЛП встречаются относительно часто, к зацикливанию они приводят лишь в исключительных случаях.

Примеры решения задач симплекс-методом

Пример 6.2. Фирма выпускает изделия четырех типов. При этом используется сырье двух видов, запасы которого соответственно 1200 и 1000 единиц. Нормы расхода сырья на изготовление каждого типа продукции, а также доход, полученный от выпуска единицы каждого типа продукции, заданы таблицей:

Источник

Тема 1.1. Особые случаи при решении задач линейного программирования:

Признак неограниченности задачи: Если существует такое k, что в z-строке и для всех i в соответствующем столбце симплекс-таблицы, то задача неограниченна.

Пусть k номер столбца, β – текущий базис, тогда , так как таблица описывает результат приведения задачи к текущему базису.

Выделим слагаемое с номером k в ограничениях и ЦФ:

Определим вектор следующим образом:

Пусть X – множество допустимых решений задачи, а – текущее базисное решение; рассмотрим луч .

Для целевой функции получаем:

Получаем, что для плана «надбавка» v к плану реализуется без дополнительных ресурсных затрат, что невозможно.

Получаем – необходимо изменение исходных данных с целью устранения данной ошибки.

2. Несовместность задачи.

Рассматривается задача в стандартной форме

Здесь столбцы a j матрицы A описывают технологические способы, элементы вектора b – запас ресурсов или обязательство (цели) по их производству.

В данной формулировке несовместность задачи означает, что применяемые в модели технологии при имеющихся ресурсах не обеспечивают выполнение обязательств и достижение целей.

Так как реальная система как то работает, то несовместность задачи показывает, что проект (модель) нуждается в доработке.

Направления совершенствования модели:

Изменяем правые части ограничений задачи:

Насколько нужно увеличить каждое b_i, чтобы задача стала разрешимой.

Вводим вектор переменных «надбавок» .

где r_i ≥ 0 – «стоимость» изменения правой части.

Важно: «стоимость» должна быть соизмеримой с исходной целевой функцией.

Пусть есть k_i способов увеличения b_i. При этом способ k может увеличить b_i не более чем на с удельными затратами . Также пусть более дешевые способы имеют меньшие номера:

Задача запишется следующим образом:

Утверждение: Если в оптимальном решении последней задачи z_i k > 0, то z_i k ` = d<sub>i</sub> k ` для всех k` k (способ применяется только после того, как исчерпаны возможности более дешевых способов).

Доказательство: Пусть в оптимальном решении задачи для некоторых k` k имеем z<sub>i</sub> k > 0, и z<sub>i</sub> k ` d_i k ` . Тогда существует такое δ >0, что z<sub>i</sub> k – δ > 0 и z<sub>i</sub> k ` + δ d_i k ` . Заменяя в условиях задачи z<sub>i</sub> k на z<sub>i</sub> k – δ, а z<sub>i</sub> k ` на z_i k ` + δ, видим, что все они выполняются. Но при этом значение целевой функции выросло на величину δ(r<sub>i</sub> k – r<sub>i</sub> k` ) . А это противоречит оптимальности решения.

В некотором роде рассмотренные способы изменения правых частей сводятся к задаче добавления нового технологического способа производства.

Возникает вопрос: каким условиям должен соответствовать технологический способ, добавляемый в модель с целью устранения несовместности?

Рассматривается задача P в канонической форме:

c · x → max при Ax = b, x ≥ 0.

Будем считать, что вектор b ≥ 0.

Решение данной задачи происходит с симплекс-метода, с поиска исходного БДР методом искусственного базиса: рассматривается вспомогательная задача P₁, которая всегда разрешима:

– Σ_i t_i → max при Ax + t = b, x ≥ 0, t ≥ 0.

Пусть f₁ – оптимальное решение задачи P₁. | f₁| указывает на минимальную достижимую величину «суммарного невыполнения» ограничений задачи P. Если задача P совместна, то f₁ = 0 , иначе f₁ < 0.

Устранение несовместности задачи – введение такого технологического способа, который повысит значение f₁ (в идеале до нуля).

Рассмотрим задачу P₁ * , двойственную к вспомогательной:

h(y) = b · y → min при yA ≥ 0, y_i ≥ –1 для всех i.

Так как задача P₁ разрешима, то и двойственная к ней будет иметь решение y * и h(y * ) = f₁.

Предположим, что в исходную задачу вводится новый технологический способ: переменная x ≥ 0 с коэффициентами a_i в ограничениях и c – в целевой функции. Аналогично строится вспомогательная задача P₂.

Она будет отличаться от P₁ введенной дополнительной переменной с теми же коэффициентами в ограничениях и нулевым коэффициентом в ЦФ.

Пусть x допустимое решение задачи P₁, тогда решение (x, x) при x = 0 – допустимо в P₂. Задача P₂ совместна. Двойственная к ней P₂ * – также разрешима.

Отличие задачи P₂ * от задачи P₁ * в ограничении:

Задачи P₂ и P₂ * разрешимы одновременно по первой теореме двойственности. Их целевые функции имеют одинаковые значения f₂.

Пусть Y₁ и Y₂ – множества допустимых решений задач P₁ * и P₂ * соответственно. Поскольку любое дополнительное ограничение сужает область поиска решения, то Y₁ Y₂.Поэтому f₁ ≤ f₂ – чем шире области минимизации (Y₁), тем меньше минимум.

Если решение задачи P₁ * удовлетворяет условию (*), то оно также является допустимым решением задачи P₂ * : y * Y₂ и f₂ = min_Y2 h(y) ≤ h(y * ) = f₁

Так как нам нужно, чтобы при добавлении способа значение целевой функции задачи P₁ повышалось (f₁ f₂), то, c учетом вышеупомянутого замечания, необходимо, чтобы условие (*) не выполнялось.

Утверждение: Для того, чтобы в несовместной задаче P с неотрицательным вектором b после введения нового технологического способа (a₁,…,a_m, c) задача стала совместной, коэффициенты a_i должны удовлетворять условию

где y_i * – двойственные оценки вспомогательной задачи P₁.

Замечание: Указанное в утверждении условие необходимо, но, вообще говоря, недостаточно, чтобы при введении нового технологического способа задача стала совместной (потребуется введение нескольких дополнительных технологических способов).

Источник

Читайте также:  Исип колледж информатики и программирования