Нелинейное программирование вогнутое программирование
Нелинейное программирование — обобщение случая линейного программирования, когда критерий — нелинейная функция решений с нелинейными ограничениями. Общих методов решения здесь не существует. Более или менее приемлемые способы решения имеются для случая, когда функция критерия К и ограничения — вогнутые функции и когда К — квадратичная функция решений, а ограничения линейны (квадратичное программирование). [c.308]
Если хотя бы одна из этих функций — нелинейная или содержит произведения искомых переменных, то соответствующая задача — это задача нелинейного программирования. Среди них наиболее изучены задачи выпуклого программирования, в результате решения которых определяют минимум выпуклой (или максимум вогнутой) функции, заданной на выпуклом замкнутом множестве. [c.104]
Тем самым приходим к задаче нелинейного программирования с линейными ограничениями (4.2), (4.3) и вогнутой целевой функцией. Воспользуемся методом Лагранжа, причем так, как это было сделано в [58]. Построим функцию [c.104]
| Рис. В.4. Задачи вогнутого и выпуклого программирования | 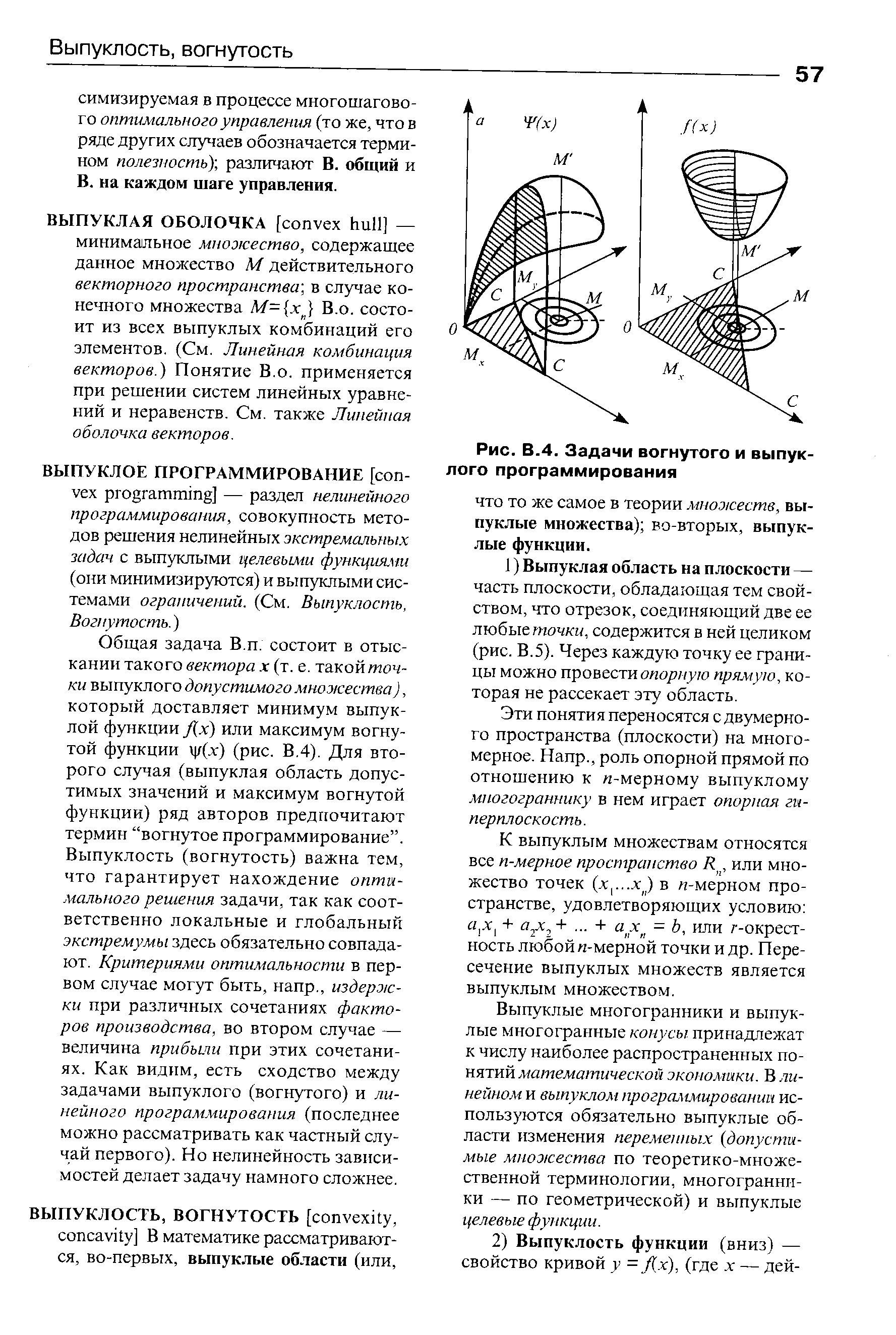 |
В зависимости от вида используемых критериев оптимальности целевых функций или функционалов) и ограничений модели (множества допустимых решений) различают скалярную О., векторную О., многокритериальную О., стохастическую О. (см. Стохастическое программирование), гладкую и негладкую (см. Гладкая функция), дискретную и непрерывную (см. Дискретность, Непрерывность), выпуклую и вогнутую (см. Выпуклость, вогнутость) и др. Численные методы О., т.е. методы построения алгоритмов нахождения оптимальных значений целевых функций и соответствующих точек области допустимых значений,—развитый отдел современной вычислительной математики. См. Оптимальная задача. [c.247]
Задачи, в к-рых целевая функция / или функции /, ограничений нелинейно зависит от переменных, паз. задачами п е л и н е ii н о г о п р о г р а м м п-]) о в а п п я. Ii ним относятся задачи выпуклого программирования, где функции /к (/ -Н, 1,. . ., ц) — вогнутые, т.е. удовлетворяют при всех ii ((he ii 1) и для любой пары точек х п. / неравенствам [c.407]
Нужно иметь в виду, что изложенный метод неприменим при отсутствии условия выпуклости функции. В этом случае в план может попасть, например, выпуск третьей тысячи изделий, а выпуск первых двух тысяч не попадет в него. Иначе говоря, план будет нереальным. В случае выпуклости такого не произойдет выпуск первых тысяч изделий как более выгодный обязательно войдет в план. Мы сделали это замечание, поскольку, к сожалению, гипотеза о выпуклости функций очень часто оказывается неправомерной. Для большинства видов производства затраты на выпуск единицы продукции обычно уменьшаются с ростом производственных мощностей, т. е. функции /4 (xt) монотонно возрастают и вогнуты — снова общая задача нелинейного программирования. [c.103]
Поскольку выпуклые функции обладают столь полезными оптимизационными качествами, они занимают исключительно важное место в теории исследования операций. Соответствующий раздел получил название выпуклого программирования, а общая задача выпуклого программирования формулируется как проблема поиска максимума вогнутой (минимума выпуклой) функции на выпуклом множестве. [c.93]
Этими моделями описываются набор однопериодных статических представлений о выборе из одних активов, меняющихся с течением времени. В этих случаях оптимизация связана с нахождением оптимума вогнутой функции на выпуклом многограннике или в общем случае на выпуклом множестве, а следовательно, могут привлекаться стандартные программы нелинейного программирования. [c.25]
Нелинейные задачи о дополнительности и вариационные неравенства являются обобщением для многих оптимизационных постановок, таких, как задачи математического (нелинейного) программирования, минимаксные задачи и задачи о седловой точке выпукло-вогнутых функций, задачи поиска равновесия в играх п лиц и др. Многие развиваемые для их решения итерационные методы могут быть с успехом применены и к линейным задачам о дополнительности. [c.30]
Третий пример связан с поиском седловых точек выпукло-вогнутых функций (и теми задачами из теории игр и математического программирования, которые сводятся к такому поиску). Пусть X и Y — непустые замкнутые выпуклые подмножества W1 и Rm соответственно, / W1 х Rm —> R — дифференцируемая числовая функция двух векторных аргументов. Седловой точкой функции f(x,y) относительно области X х Y называется пара (х,у) е X х У, удовлетворяющая неравенствам [c.31]
Общая задача В.п. состоит в отыскании такого вектора х (т. е. такойточ-ки выпуклого допустимого множества), который доставляет минимум выпуклой функции J[x) или максимум вогнутой функции у(х) (рис. В.4). Для второго случая (выпуклая область допустимых значений и максимум вогнутой функции) ряд авторов предпочитают термин «вогнутое программирование». Выпуклость (вогнутость) важна тем, что гарантирует нахождение оптимального решения задачи, так как соответственно локальные и глобальный экстремумы здесь обязательно совпадают. Критериями оптимальности в первом случае могут быть, напр., издержки при различных сочетаниях факторов производства, во втором случае — величина прибыли при этих сочетаниях. Как видим, есть сходство между задачами выпуклого (вогнутого) и линейного программирования (последнее можно рассматривать как частный случай первого). Но нелинейность зависимостей делает задачу намного сложнее. [c.57]
Рассмотрим итеративный метод решения задачи (4.15) вогнутого программирования, представляющий собой обобщение метода Гаусса — Зейделя покоординатного спуска. В [83] метод Гаусса — Зей-деля распространен на случай, когда на каждом шаге производится оптимизация не по отдельным переменным, а по векторам, составляющие которых — некоторые подмножества множества переменных задачи. Задача (4.15) не укладываетя в класс задач, для решения которых в [83] обосновано обобщение метода покоординатного спуска. Векторы X/j( oh ) — аргументы функции q (q). Иными словами, если стоимость вектора потребления (q) в ценах р не превосходит стоимости вектора С(р), то стоимость вектора С(р) в ценах q больше стоимости (q). Основанием для признания этой аксиомы является следующее рассуждение. Вектор (q) удовлетворяет бюджетному ограничению при ценах р, но потребитель отвергает его и выбирает С(р), выявляя тем самым, что для него С(р) лучше (q). Но при ценах q выбирается вектор (q), значит, в этом случае выбор С(р) невозможен.5 [c.494]
Из нелинейных задач выделяются задачи выпуклого программирования. В этих задачах вычисляется максимум вогнутой функции на выпуклом множестве1. Решение задач выпуклого программирования значительно упрощается, если исходные условия (ограничения) представлены в виде линейных равенств и неравенств. К числу подобных задач относятся задачи квадратического программирования. [c.164]
Динамическое программирование непосредственно ориентировано на решение дискретных задач однако его можно использовать и для задач, в которых все переменные непрерывны. В этих случаях непрерывная область пространства решений дискретизуется и отыскивается оптимальное управление. Затем в его окрестности используется более мелкая сетка, и т.п. Непрерывные функции заменяются аппроксимациями по ряду дискретных точек. Доказанная вогнутость или выпуклость функций дохода (затрат) существенно ограничивают перебор. [c.149]
Задача максимизации ( .59) — (9.61) называется задачей выпуклого программировании я в том случае, когда все функции Ф,-(Л1) являются вылуклывми, а целевая функция f(M) — вогнутой на ИЛ».. [c.230]