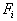- 2. Различные виды записи задач линейного программирования. Переход от одного вида задачи линейного программирования к другому.
- Симплексный метод
- Алгоритм симплексного метода решения задач линейного программирования
- Общая, стандартная и основная задачи линейного программирования
- Геометрическая интерпретация задачи линейного программирования
- Линейное программирование
- 1.1. Примеры моделей, приводящих к задачам линейного программирования
- Задача о диете
2. Различные виды записи задач линейного программирования. Переход от одного вида задачи линейного программирования к другому.
Во многих областях практической деятельности человека возникают своеобразные задачи математического программирования, для которых характерны следующие особенности:
− целевая функция является линейной функцией переменных составляющих план задачи математического программирования;
− система ограничений (2.2) имеет вид системы линейных уравнений и/или неравенств.
Такие задачи называют задачами линейного программирования.
Существует несколько форм записи задач линейного программирования. Рассмотрим их.
1. Общая форма записи задачи линейного программирования: необходимо найти экстремальное значение целевой функции
на некоторые неизвестные могут быть наложены условия неотрицательности:
Здесь (и везде далее) заданные числа
2. Каноническая форма записи задачи линейного программирования: необходимо найти экстремальное значение целевой функции (4.1) при ограничениях
На все неизвестные наложены условия неотрицательности:
3. Симметричная форма записи задачи линейного программирования. Здесь принято выделять две стандартные задачи − задачу максимизации и задачу минимизации.
3.1. Стандартная задача максимизации: необходимо найти максимальное значение целевой функции (4.1) при ограничениях
и условиях неотрицательности (4.2).
3.2. Стандартная задача минимизации: необходимо найти минимальное значение целевой функции (4.1) при ограничениях
и условиях неотрицательности (4.2).
Симплексный метод
Данный метод является методом целенаправленного перебора опорных решений задачи линейного программирования. Он позволяет за конечное число шагов либо найти оптимальное решение, либо установить, что оптимальное решение отсутствует.
Основное содержание симплексного метода заключается в следующем:
- Указать способ нахождения оптимального опорного решения
- Указать способ перехода от одного опорного решения к другому, на котором значение целевой функции будет ближе к оптимальному, т.е. указать способ улучшения опорного решения
- Задать критерии, которые позволяют своевременно прекратить перебор опорных решений на оптимальном решении или следать заключение об отсутствии оптимального решения.
Алгоритм симплексного метода решения задач линейного программирования
Для того, чтобы решить задачу симплексным методом необходимо выполнить следующее:
- Привести задачу к каноническому виду
- Найти начальное опорное решение с «единичным базисом» (если опорное решение отсутствует, то задача не имеет решение ввиду несовместимости системы ограничений)
- Вычислить оценки разложений векторов по базису опорного решения и заполнить таблицу симплексного метода
- Если выполняется признак единственности оптимального решения, то решение задачи заканчивается
- Если выполняется условие существования множества оптимальных решений, то путем простого перебора находят все оптимальные решения
Общая, стандартная и основная задачи линейного программирования
Определение 1. Общей задачей ЛП называется задача нахождения максимального (минимального) значения линейной целевой функции 













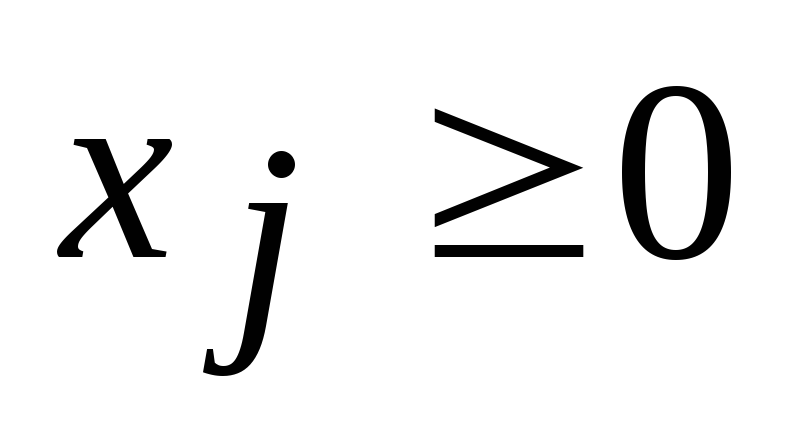







- Задачу минимизации функции можно свести к задаче максимизации, и, наоборот, путем замены знаков коэффициентов
на противоположные, поскольку
.
- Ограничения-неравенства (2) можно заменить эквивалентными ограничениями-равенствами путем введения дополнительных неотрицательных переменных следующим образом:
Ограничение-неравенство вида 




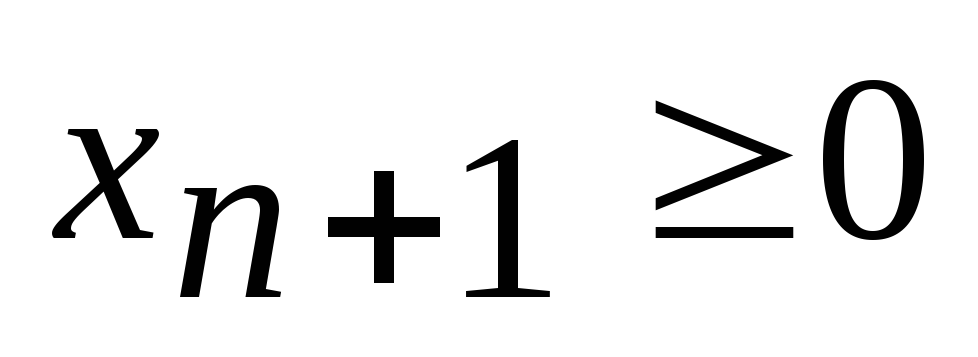
- Каждое ограничение-равенство вида (3) можно записать в виде двух неравенств
.
- Переменная
, неограниченная условием неотрицательности вида (4), можно заменить разностью двух дополнительных неотрицательных переменных:
,
,
.
-
Геометрическая интерпретация задачи линейного программирования
Рассмотрим задачу, состоящую в определении максимального значения функции: 









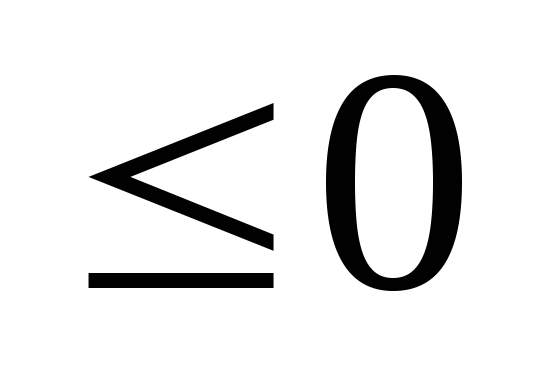


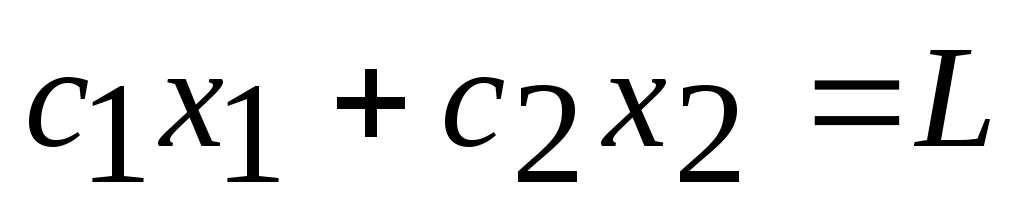

Линейное программирование
1.1. Примеры моделей, приводящих к задачам линейного программирования
Линейное программирование является одной из основных частей того раздела современной математики, который получил название математического программирования. В общей постановке задачи этого раздела выглядят следующим образом.
Имеются какие-то переменные 


В зависимости от вида функции и области G и различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. Подробнее об этом будет сказано в заключении.
Линейное программирование характеризуется тем, что
является линейной функцией переменных ;
б) область G определяется системой линейных равенств или неравенств.
Чтобы понять, откуда берутся задачи линейного программирования, рассмотрим некоторые, уже ставшие классическими, примеры подобных задач.
Задача о диете
Задача о диете возникает при составлении наиболее экономного (т.е. наиболее дешевого) рациона питания животных, удовлетворяющего определенным медицинским требованиям.
Предположим, что в нашем распоряжении имеется n продуктов питания (сено, зерно, комбикорм, соль и т.д.). Обозначим эти продукты через
есть стоимость единицы веса (например,
стоимость одного килограмма) продукта .
Рациональная диета должна доставлять животному определенные компоненты (белки, жиры, углеводы, витамины, микроэлементы и т.д.). Обозначим эти компоненты через . Тогда можно составить таблицу — справочник, указывающую, какое количество каждого компонента имеется в единице веса каждого продукта.




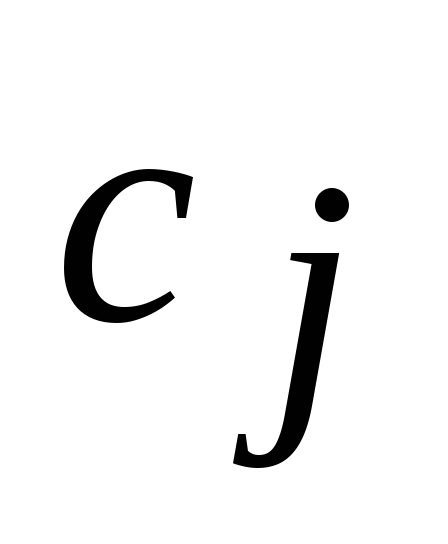 на противоположные, поскольку
на противоположные, поскольку .
. .
. , неограниченная условием неотрицательности вида (4), можно заменить разностью двух дополнительных неотрицательных переменных:
, неограниченная условием неотрицательности вида (4), можно заменить разностью двух дополнительных неотрицательных переменных: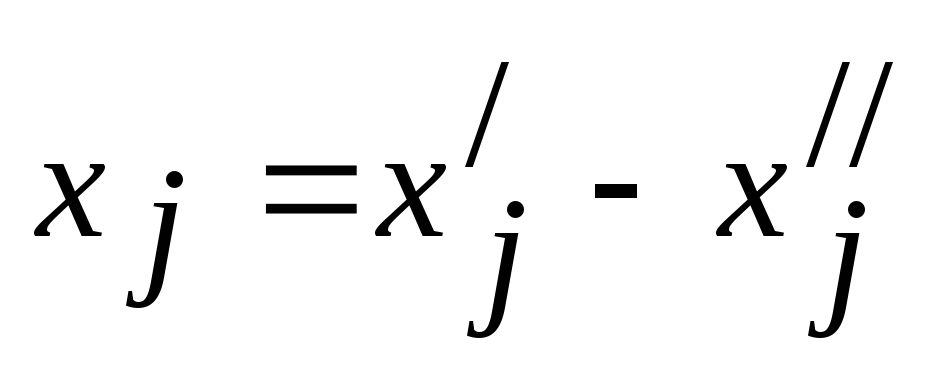 ,
, ,
,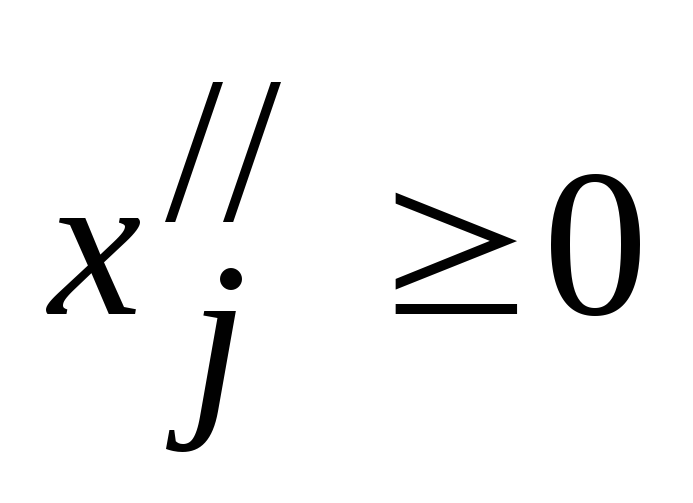 .
.