Найти значение производной python

Дифференцирование и интегрирование функций#

В рамказ компьютерной арифметики предельный переход осуществить невозможно, поэтому в целях аппроксимации производной нередко вместо предела при \(h \to 0\) подставляют очень малое \(h\) :

Такая аппроксимация производной называется правой разностной производной. Можно показать, что асимптотическая погрешность вычисления производной таким способом имеет вид \(o(h)\) , т.е. уменьшая шаг \(h\) можно добиться любой точности вычисления производной. Более распространенна центральная разнастная производная, определяемая выражением

Её асимптотическая погрешность имеет вид \(o(h^2)\) , а значит уменьшая шаг \(h\) в 2 раза, можно ожидать уменьшение погрешности вычисления производной в 4 раза.

Аналогичным образом можно определить аппроксимацию производной любого порядка. Метод scipy.misc.derivative в SciPy вычисляет разностную производную произвольного порядка (опциональный параметр n ).

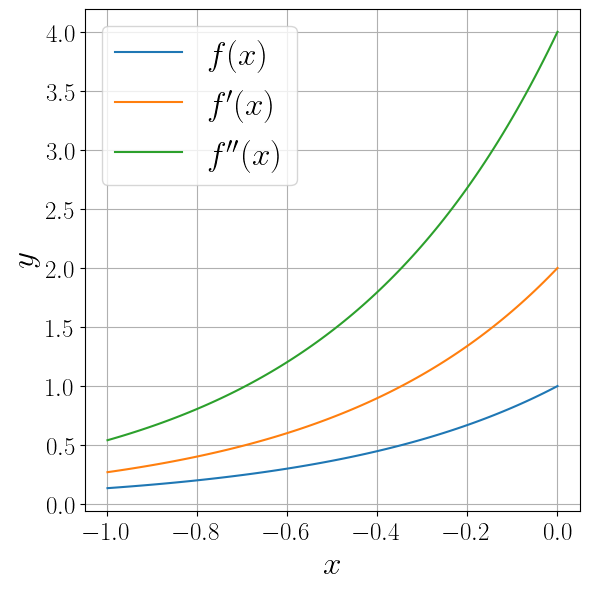
Продемонстрируем его применение на примере функции \(f(x) = e^\) .

from scipy.misc import derivative import numpy as np def f(x): return np.exp(2. * x) fig, ax = plt.subplots(figsize=(6, 6), layout="tight") x = np.linspace(-1, 0, 100) labels = ("$f(x)$", "$f'(x)$", "$f''(x)$") for n, label in enumerate(labels): y = derivative(f, x, n=n, dx=1e-3, order=2*n+1) if order > 0 else f(x) ax.plot(x, y, label=label) ax.set_xlabel("$x$") ax.set_ylabel("$y$") ax.legend() ax.grid() 

Аналитическое дифференцирование#

Ряд современных библиотек умеет вычислять производные от своих методов. Например, библиотека autograd.

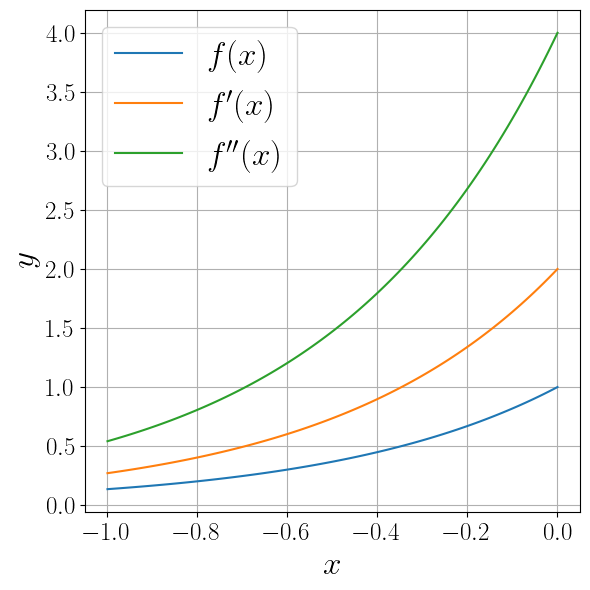
Обратите внимание, что для аналитического вычисления производной средствами библиотеки autograd , необходимо вместо библиотеки NumPy использовать модуль autograd.numpy .

from autograd import numpy as np from autograd import elementwise_grad fig, ax = plt.subplots(figsize=(6, 6), layout="tight") x = np.linspace(-1, 0, 100) labels = ("$f(x)$", "$f'(x)$", "$f''(x)$") funcs = (f, elementwise_grad(f), elementwise_grad(elementwise_grad(f))) for order, (label, func) in enumerate(zip(labels, funcs)): ax.plot(x, func(x), label=label) ax.set_xlabel("$x$") ax.set_ylabel("$y$") ax.legend() ax.grid() 

Интегрирование функций#

Подмодуль scipy.integrate позволяет приближенно вычислять значение определенных интегралов.

Однократные интегралы#

Функция scipy.integrate.quad позволяет проинтегрировать функцию \(f\colon \mathbb \to \mathbb\) . Вызов функции quad(f, a, b) приближенно находит значение интеграла

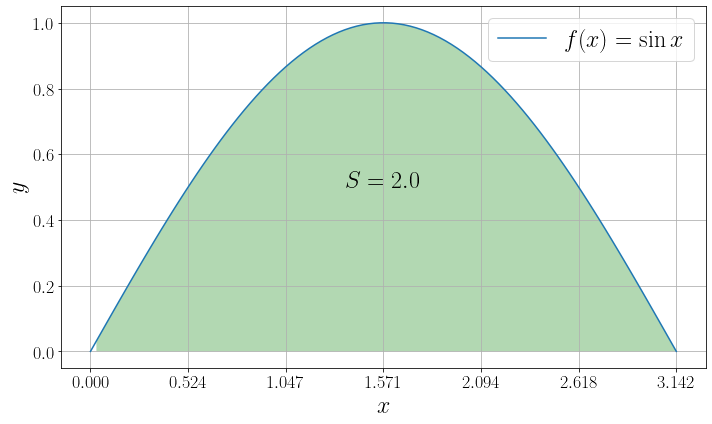
В качестве примера найдем численно значение интеграла

import numpy as np from scipy import integrate from matplotlib import pyplot as plt f = np.sin a, b = 0, np.pi I, _ = integrate.quad(f, 0, np.pi) x = np.linspace(0, np.pi, 100) y = f(x) fig, ax = plt.subplots(figsize=(10, 6), layout="tight") ax.plot(x, y, label=r"$f(x)=\sin x$") ax.set_xlabel("$x$") ax.set_ylabel("$y$") ax.fill_between(x, np.zeros_like(x), y, where=(y>0), facecolor='green', alpha=0.30) ax.set_xticks(np.linspace(0, np.pi, 7)) ax.text(np.pi/2, 0.5, fr"$S = I>$", fontdict="size": 24, "ha": "center">) ax.legend() ax.grid() 

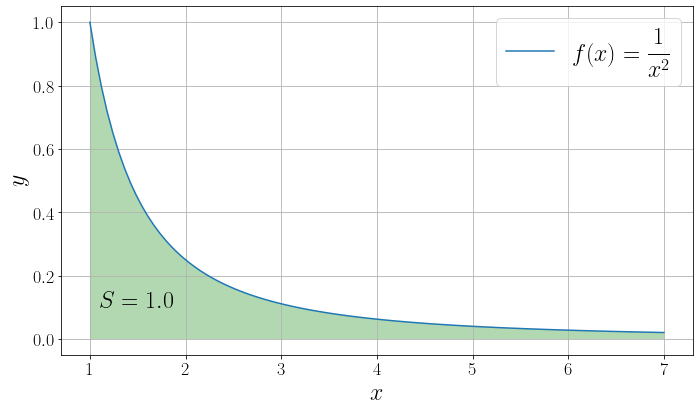
Параметры \(a\) и \(b\) могут принимать значения -inf и +inf , чтобы брать несобственные интегралы. Продемонстрируем это на примере интеграла

def f(x): return 1. / np.square(x) a, b = 1, np.inf I, _ = integrate.quad(f, a, b) x = np.linspace(a, 7, 100) y = f(x) fig, ax = plt.subplots(figsize=(10, 6), layout="tight") ax.plot(x, y, label=r"$f(x)=\dfrac $") ax.set_xlabel("$x$") ax.set_ylabel("$y$") ax.fill_between(x, np.zeros_like(x), y, where=(y>0), facecolor='green', alpha=0.30) ax.set_xticks(np.linspace(1, 7, 7)) ax.text(1.5, 0.1, fr"$S = I>$", fontdict="size": 24, "ha": "center">) ax.legend() ax.grid() 

Однако численное взятие несобственных интегралов отнюдь не тривиальная задача. Например, интеграл Френеля $ \( \int\limits_0^\infty \sin x^2 \, dx = \sqrt<\dfrac<\pi>> \) $

просто так вычислить не удастся.

def f(t): return np.sin(t**2) I, _ = integrate.quad(f, 0, np.inf) print(I) 

C:\Users\fadeev\AppData\Local\Temp/ipykernel_8252/3166585030.py:4: IntegrationWarning: The integral is probably divergent, or slowly convergent. I, _ = integrate.quad(f, 0, np.inf)

Интегралы большей кратности#

Функция scipy.integrate.dblquad позволяет вычислять интегралы вида

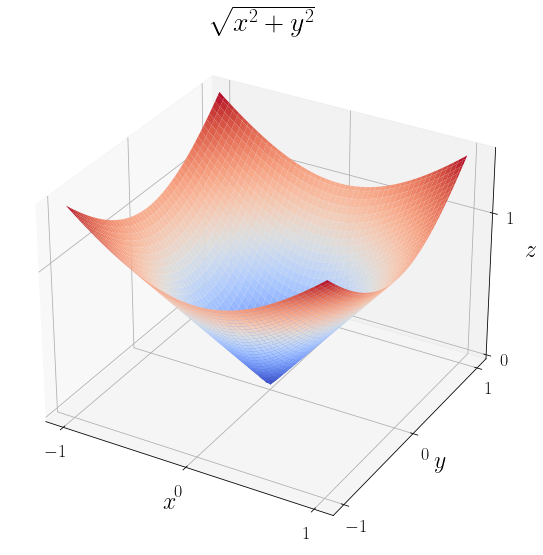
В качестве примера возьмём интеграл функции \(f = \sqrt\) в области \(D\) совпадающей с кругом единичного радиуса с центром в начале:

import numpy as np from scipy import integrate from matplotlib import pyplot as plt def h(x): return np.sqrt(1 - x**2) def g(x): return -h(x) def f(x, y): return np.sqrt(x**2 + y**2) a, b = -1, 1 I, _ = integrate.dblquad(f, -1, 1, g, h) x = np.linspace(a, b, 100) y = np.linspace(a, b, 100) x, y = np.meshgrid(x, y) z = f(x, y) fig, ax = plt.subplots(figsize=(8, 8), layout="tight", subplot_kw="projection": "3d">) ax.plot_surface(x, y, z, cmap="coolwarm") ax.set_xlabel("$x$") ax.set_ylabel("$y$") ax.set_zlabel("$z$") ax.set_xticks([-1, 0, 1]) ax.set_yticks([-1, 0, 1]) ax.set_zticks([0, 1]) ax.set_title(r"$\sqrt$") print(f"Вычисленное значение интеграла: I>, точное значение: 2*np.pi/3>.") 

Вычисленное значение интеграла: 2.0943951023924106, точное значение: 2.0943951023931953.

Трехкратные интегралы вида

можно вычислить методом integrate.tplquad. Интеграл произвольной кратности можно вычислить методом integrate.tplquad.

Источник

Производные в Python с использованием симпы

Как рассчитать производные в Python? В этой статье мы будем использовать Sympy Sympy Python, чтобы играть с производными.

Производные в Python с использованием симпы

Как рассчитать производные в Python? В этой статье мы будем использовать Sympy Sympy Python, чтобы играть с производными.

Какие производные?

Производные являются фундаментальными инструментами исчисления. Это очень полезно для оптимизации функции потери с Градиентный спуск в Машинное обучение возможно только из-за производных.

Предположим, у нас есть функция y = F ( X ), который зависит от х Затем вывод этой функции означает скорость, при которой значение y функции изменяется с изменением х Отказ

Это ни отнюдь означает статью о основах производных, она не может быть. Исчисление – это другой зверь, который требует особого внимания. Я предполагаю, что у вас есть какой-то опыт в исчислении. Эта статья предназначена для продемонстрирования того, как мы можем дифференцировать функцию с использованием симпы-библиотеки.

Решение производных в Python с использованием Sympy

Sympy – библиотека Python для символической математики.

Он стремится стать полнофункциональной системой компьютерной алгебры (CAS), сохраняя максимально простую код, остынет, не так ли.

1. Установите Sympy, используя PIP

Sympy имеет больше используемых, чем просто расчет производных, но на данный момент мы сосредоточимся на производных.

Беги PIP Установить Sympy Для установки с помощью Диспетчер пакетов PIP Отказ

2. Решение дифференциала с Sympy Diff ()

Для дифференциации Sympy предоставляет нам Различать способ вывода производной функции.

Посмотрим, как мы можем достичь этого, используя Sympy.

#Importing sympy from sympy import * # create a "symbol" called x x = Symbol('x') #Define function f = x**2 #Calculating Derivative derivative_f = f.diff(x) derivative_f

Объявление символа похоже на то, что наша функция имеет переменную «X» или просто функция зависит от x.

3. Решение производных в Python

Теперь для расчета производной функции на Sympy есть лямбдифицировать Функция, в которой мы передаем символ и функцию.

from sympy import * # create a "symbol" called x x = Symbol('x') #Define function f = x**2 f1 = lambdify(x, f) #passing x=2 to the function f1(2)

Основные производные правила в Python Sympy

Есть определенные правила, которые мы можем использовать для расчета производной дифференцируемых функций.

Некоторые из наиболее встречающихся правил:

Давайте погрузимся в то, как мы можем использовать Simpy для расчета производных, подразумеваемых правилами общей дифференцировки.

1. Правило питания

Пример, функция у нас есть:

Это производное будет: (5-1) 4.

import sympy as sym #Power rule x = sym.Symbol('x') f = x**5 derivative_f = f.diff(x) derivative_f

2. Правило продукта

Пусть u (x) и v (x) будут дифференцируемыми функциями. Тогда продукт функций u (x) v (x) также дифференцируемый.

import sympy as sym #Product Rule x = sym.Symbol('x') f = sym.exp(x)*sym.cos(x) derivative_f = f.diff(x) derivative_f

3. Правило цепочки

Правило цепочки рассчитывает производное состав функций.

• Скажем, у нас есть функция (G (x))
• Затем в соответствии с правилом цепи: ‘(g (x)) g’ (x)
• Пример: (х ** 2)

Этот процесс может быть расширен для коэффициента правила также. К настоящему времени необходимо очевидно, что только функция меняется, в то время как процесс приложения остается прежним, остальное заботится о самой библиотеке.

import sympy as sym #Chain Rule x = sym.Symbol('x') f = sym.cos(x**2) derivative_f = f.diff(x) derivative_f

Производные многомерные функции с использованием Sympy

Примеры, которые мы видели выше, имели одну переменную. Но мы более склонны столкнуться с функциями, имеющими более одной переменной в них. Такие производные, как правило, называются частичными производными.

Частичное производное многомерной функции представляет собой производное относительно одной переменной со всеми другими переменными.

Давайте частично отличаем вышеупомянутые производные в Python W.r.t x

import sympy as sym #Derivatives of multivariable function x , y = sym.symbols('x y') f = x**4+x*y**4 #Differentiating partially w.r.t x derivative_f = f.diff(x) derivative_f

Мы используем Символы Метод, когда количество переменных составляет более 1. Теперь, дифференцируйте производные в Python частично W.R.T Y

import sympy as sym #Derivatives of multivariable function x , y = sym.symbols('x y') f = x**4+x*y**4 #Differentiating partially w.r.t y derivative_f = f.diff(y) derivative_f

Код точно похоже, но теперь Y передается как аргумент ввода в Различать метод.

Мы можем выбрать частично дифференцировать функцию сначала w.r.t x, а затем y.

import sympy as sym #Derivatives of multivariable function x , y = sym.symbols('x y') f = x**4+x*y**4 #Differentiating partially w.r.t x and y derivative_f = f.diff(x,y) derivative_f

Заключение

Эта статья ни в коем случае не было дискурсом о производных или как мы можем решать производные в Python, но статью о том, как мы можем использовать пакеты Python для выполнения разграничения на функции. Производные потрясающие, и вы обязательно должны получить идею позади него, так как они играют решающую роль в машинном обучении и за его пределами.

Читайте ещё по теме:

Источник

Вычисление производной

Для вычисления производных будем использовать библиотеку SymPy. Это библиотека с открытым исходным кодом, полностью написанная на языке Python. Разрабатывается как система компьютерной алгебры.

Подключение SymPy

Вначале нам необходимо установить библиотеку. Для этого в терминале (командной строке) следует ввести команду: pip install sympy .

Для подключения библиотеки в коде на Python 3 следует использовать ключевое слово import .

Чтобы не писать перед всеми функциями sympy с точкой, подключу следующим образом:

Следует обратить внимание, что в SymPy объявлено множество классов и функций, имена которых могут пересекаться с названиями в других библиотеках. Например, если используете библиотеку math, то там также есть sin , cos , pi и другие.

Формула российских дорог

Например, возьмем функцию с двумя независимыми переменными, типа поверхности y=f(x, z). Воспользуемся формулой российских дорог: y=sin(x)+0,5·z.

Перед тем как взять производную этой функции в Python, надо объявить все переменные, которые будут использоваться в ней. Для этого следует воспользоваться функцией symbols . В качестве аргумента используем строку с перечисленными через запятую или пробел названиями переменных.

После этого берем частную производную в Python 3 с помощью функции diff . Первым аргументом пишем функцию, вторым – переменную, по которой будем её дифференцировать.

Результат выводим с помощью print .

Дорога в горку

from sympy import * x, z = symbols('x z') print(diff(sin(x)+0.5*z, z)) 0.500000000000000

В результате получили 0.5. Частная производная по z положительна, следовательно, дорога в горку.

Дорога с колеёй

Теперь возьмём производную по x:

from sympy import * x, z = symbols('x z') print(diff(sin(x)+0.5*z, x)) cos(x)

Получили, что частная производная по x равна cos(x). Трактору на колею наплевать, ему важен только наклон горки.

В зависимости от задачи берем производную по нужному параметру.

В функции diff при необходимости, можно указать третьим параметром порядок дифференцирования. Так как мы вычисляли производную первого порядка, то его не указывали.

Источник