Найти минимум функции питон
Тестирование метода Хука-Дживса на функции Розенброка показало его чувствительность к выбору начальной точки поиска экстремума функции.
В этой работе, опять же на функции Розенброка, реализуется и тестируется метод Нелдера-Мида [1].
Приводится Python-реализации поиска минимума функции методом Нелдера-Мида.
При желании можно познакомиться и с Фортран-, и C#-реализациями метода Нелдера-Мида.
Замечание. Для поиска максимума нужно умножить на -1 результат, получаемый при вычислении значения оптимизируемой функции.
В качестве тестовой берется функция Розенброка:
Глобальный минимум функции равен 0.0 и находится в точке (x1, x2) = (1.0, 1.0).
При работе с функцией Розенброка для проверки используемого метода в качестве начальной часто берут точку
(-5, 10)
или точку
(-2.048, 2.048).
Приводимая программа может работать с произвольной оптимизируемой функцией.
Код, реализующий метод Нелдера-Мида, предваряет Python-программа построения графика функции Розенброка.
Вывод графика функции Розенброка
Выводится изометрическая проекция 3d-поверхности. Используется библиотека Matplotlib [2].
График показан на рис. 1.
Рис. 1. График функции Розенброка
Для его вывода употреблен следующий код:
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from matplotlib import cm
import numpy as np
# Формирование сетки
X = np.arange(-2, 2, 0.1)
Y = np.arange(-1.5, 3, 0.1)
X, Y = np.meshgrid(X, Y)
# Функция Розенброка
Z = (1.0 — X)**2 + 100.0 * (Y — X * X)**2
#
fig = plt.figure()
# Будем выводить 3d-проекцию графика функции
ax = fig.gca(projection = ‘3d’)
# Вывод поверхности
surf = ax.plot_surface(X, Y, Z, cmap = cm.Spectral, linewidth = 0, antialiased = False)
# Метки осей координат
ax.set_xlabel(‘X’)
ax.set_ylabel(‘Y’)
ax.set_zlabel(‘Z’)
# Настройка оси X
for label in ax.xaxis.get_ticklabels():
label.set_color(‘black’)
label.set_rotation(-45)
label.set_fontsize(9)
# Настройка оси Y
for label in ax.yaxis.get_ticklabels():
label.set_fontsize(9)
# Настройка оси Z
for label in ax.zaxis.get_ticklabels():
label.set_fontsize(9)
# Изометрия
ax.view_init(elev = 30, azim = 45)
# Шкала цветов
fig.colorbar(surf, shrink = 0.5, aspect = 5)
# Отображение результата (рис. 1)
plt.show()
Python-реализация метода Нелдера-Мида
Используется библиотека SciPy [3]. Реализуются два варианта вызова библиотечной процедуры оптимизации:
- Задается начальная точка поиска минимума функции.
- Задается начальный симплекс поиска минимума функции.
# Вариант 1
import numpy as np
import math # Для sqrt()
import scipy.optimize as opt
# Функция Розенброка
def Rosenbrock(X):
return (1.0 — X[0])**2 + 100.0_8 * (X[1] — X[0] * X[0] )**2
#
n = 2
x0 = np.zeros(2, dtype = float) # Вектор с двумя элементами типа float
# Начальная точка поиска минимума функции
x0[0] = -5.0
x0[1] = 10.0
xtol = 1.0e-5 # Точность поиска экстремума
# Находим минимум функции
res = opt.minimize(Rosenbrock, x0, method = ‘Nelder-Mead’, options = )
print(res)
Результат:
final_simplex: (array([[1.00000132, 1.0000028 ],
[1.00000014, 0.99999997],
[0.99999681, 0.99999355]]), array([4.38559817e-12, 9.00569749e-12, 1.05977059e-11]))
fun: 4.385598172677925e-12
message: ‘Optimization terminated successfully.’
nfev: 269 (число оценок функции)
nit: 143 (число итераций)
status: 0
success: True
x: array([1.00000132, 1.0000028 ])
# Вариант 2
import numpy as np
import math # Для sqrt()
import scipy.optimize as opt
# Функция Розенброка
def Rosenbrock(X):
return (1.0 — X[0])**2 + 100.0_8 * (X[1] — X[0] * X[0] )**2
#
# Процедура формирования начального симплекса
def makeInitialSimplex(X, L, n, initialSimplex):
qn = math.sqrt(1.0 + n) — 1.0
q2 = L / math.sqrt(2.0) * n
r1 = q2 * (qn + n)
r2 = q2 * qn
initialSimplex[0, :] = X
for j in range(n):
initialSimplex[j + 1, :] = X + r2
for i in range(n):
initialSimplex[i + 1, i] += (r1 — r2)
#
n = 2
x0 = np.zeros(2, dtype = float) # Вектор с двумя элементами типа float
# Начальная точка поиска минимума функции
x0[0] = -5.0
x0[1] = 10.0
xtol = 1.0e-5 # Точность поиска экстремума
# Начальная симплекс поиска минимума функции
initialSimplex = np.zeros((n + 1, n), dtype = float)
L = 0.4 # Длина ребра начального симплекса
# Формируем начальный симплекс
makeInitialSimplex(x0, L, n, initialSimplex)
# Находим минимум функции
res = opt.minimize(Rosenbrock, x0, method = ‘Nelder-Mead’, options = )
print(res)
Результат:
final_simplex: (array([[1.00000168, 1.00000305],
[0.99999702, 0.99999376],
[0.99999679, 0.99999416]]), array([1.18711392e-11, 1.70297440e-11, 4.41663303e-11]))
fun: 1.1871139195622139e-11
message: ‘Optimization terminated successfully.’
nfev: 255 (число оценок функции)
nit: 138 (число итераций)
status: 0
success: True
x: array([1.00000168, 1.00000305])
Литература
- Nichtrestringierte Optimierung. Numerik III, 21. Januar 2013.
- Matplotlib: Научная графика в Python. [Электронный ресурс] URL: https://pythonworld.ru/novosti-mira-python/scientific-graphics-in-python.html.
- SciPy Tutorial. Optimization. [Электронный ресурс] URL: https://docs.scipy.org/doc/scipy/reference/tutorial/optimize.html.
Метод оптимизации Нелдера — Мида. Пример реализации на Python
Метод Нелдера — Мида — метод оптимизации (поиска минимума) функции от нескольких переменных. Простой и в тоже время эффективный метод, позволяющий оптимизировать функции без использования градиентов. Метод надежен и, как правило, показывает хорошие результаты, хотя и отсутствует теория сходимости. Может использоваться в функции optimize из модуля scipy.optimize популярной библиотеки для языка python, которая используется для математических расчетов.
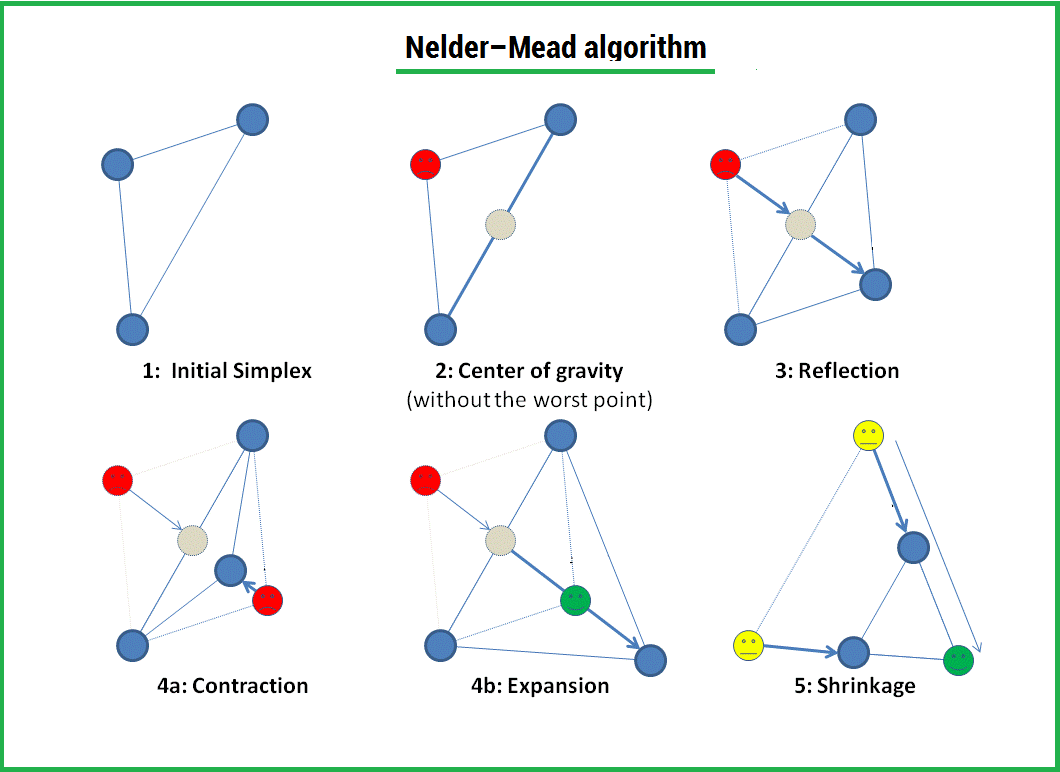
Алгоритм заключается в формировании симплекса (simplex) и последующего его деформирования в направлении минимума, посредством трех операций:
1) Отражение (reflection);
2) Растяжение (expansion);
3) Сжатие (contract);
Симплекс представляет из себя геометрическую фигуру, являющуюся n — мерным обобщением треугольника. Для одномерного пространства — это отрезок, для двумерного — треугольник. Таким образом n — мерный симплекс имеет n + 1 вершину.
Алгоритм
1) Пусть функция, которую необходимо оптимизировать. На первом шаге выбираем три случайные точки (об этом чуть позже) и формируем симплекс (треугольник). Вычисляем значение функции в каждой точке: , , .
Сортируем точки по значениям функции в этих точках, таким образом получаем двойное неравенство:
Мы ищем минимум функции, а следовательно, на данном шаге лучшей будет та точка, в которой значение функции минимально. Для удобства переобозначим точки следующим образом:
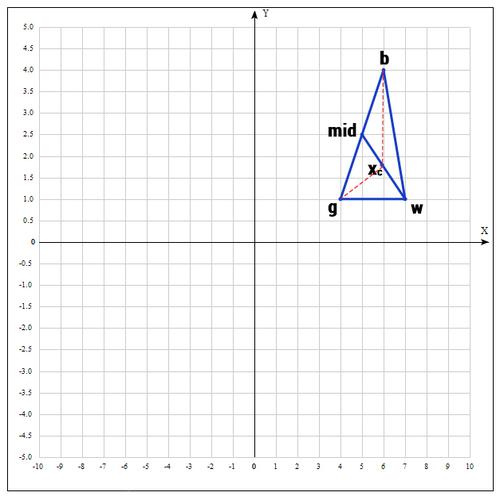
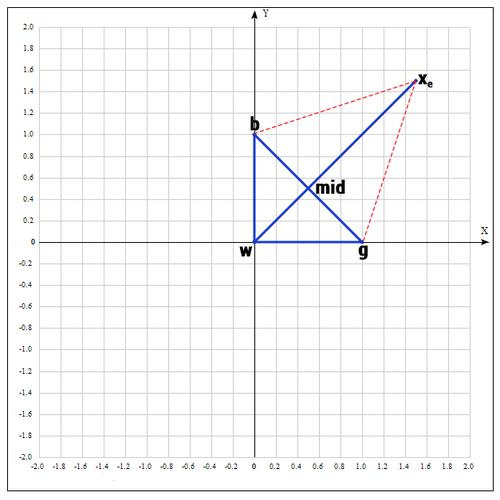
b = , g = , w = , где best, good, worst — соответственно.
2) На следующем шаге находим середину отрезка, точками которого являются g и b. Т.к. координаты середины отрезка равны полусумме координат его концов, получаем:
В более общем виде можно записать так:
3) Применяем операцию отражения:
Находим точку , следующим образом:
Т.е. фактически отражаем точку w относительно mid. В качестве коэффициента берут как правило 1. Проверяем нашу точку: если , то это хорошая точка. А теперь попробуем расстояние увеличить в 2 раза, вдруг нам повезет и мы найдем точку еще лучше.
4) Применяем операцию растяжения:
Находим точку следующим образом:
В качестве γ принимаем γ = 2, т.е. расстояние увеличиваем в 2 раза.
Если , то нам повезло и мы нашли точку лучше, чем есть на данный момент, если бы этого не произошло, мы бы остановились на точке .
Далее заменяем точку w на , в итоге получаем:
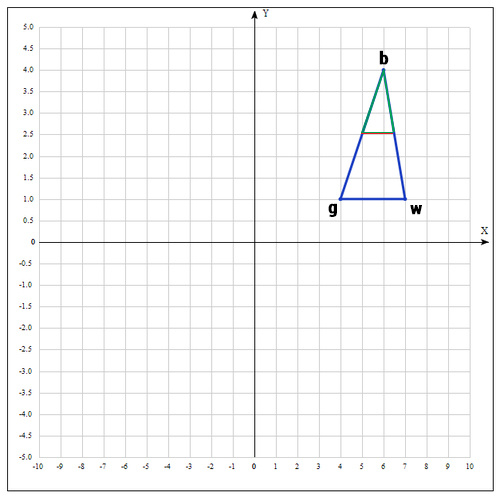
5) Если же нам совсем не повезло и мы не нашли хороших точек, пробуем операцию сжатия.
Как следует из названия операции мы будем уменьшать наш отрезок и искать хорошие точки внутри треугольника.
Пробуем найти хорошую точку :
Коэффициент β принимаем равным 0.5, т.е. точка на середине отрезка wmid.
Существует еще одна операция — shrink (сокращение). В данном случае, мы переопределяем весь симплекс. Оставляем только «лучшую» точку, остальные определяем следующим образом:
Коэффициент δ берут равным 0.5.
По существу передвигаем точки по направлению к текущей «лучшей» точке. Преобразование выглядит следующим образом:
Необходимо отметить, что данная операция дорого обходится, поскольку необходимо заменять точки в симплексе. К счастью было установлено, при проведении большого количества экспериментов, что shrink — трансформация редко случается на практике.
Алгоритм заканчивается, когда:
1) Было выполнено необходимое количество итераций.
2) Площадь симплекса достигла определенной величины.
3) Текущее лучшее решение достигло необходимой точности.
Как и в большинстве эвристических методов, не существует идеального способа выбора инициализирующих точек. Как уже было сказано, можно брать случайные точки, находящиеся недалеко друг от друга для формирования симплекса; но есть решение и получше, которое используется в реализации алгоритма в MATHLAB:
Выбор первой точки поручаем пользователю, если он имеет некоторое представление о возможном хорошем решении, в противном случае выбирается случайным образом. Остальные точки выбираются исходя из , на небольшом расстоянии вдоль направления каждого измерения:
где — единичный вектор.
определяется таким образом:
= 0.05, если коэффициент при в определении не нулевой.
= 0.00025, если коэффициент при в определении нулевой.
Пример:
Найти экстремум следующей функции:
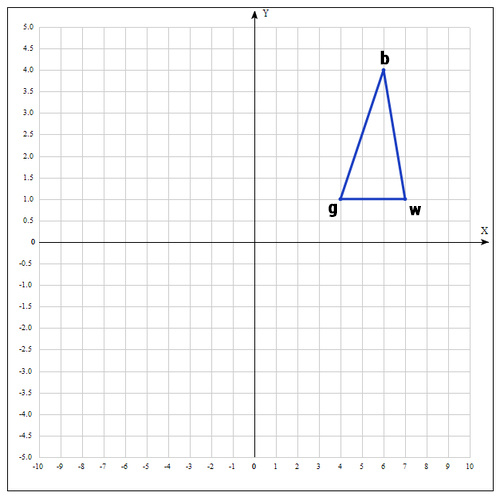
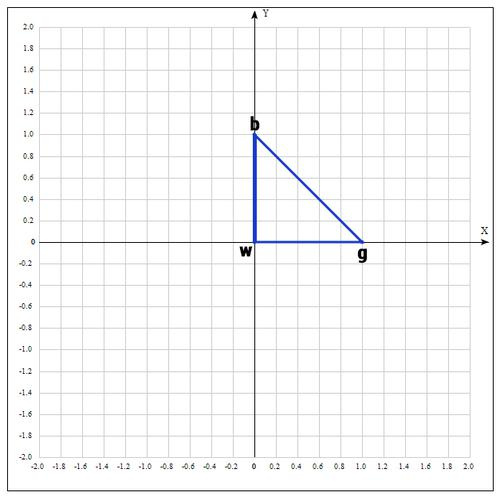
В качестве начальных возьмем точки:
Вычислим значение функции в каждой точке:
Переобозначим точки следующим образом:
Находим середину отрезка bg:
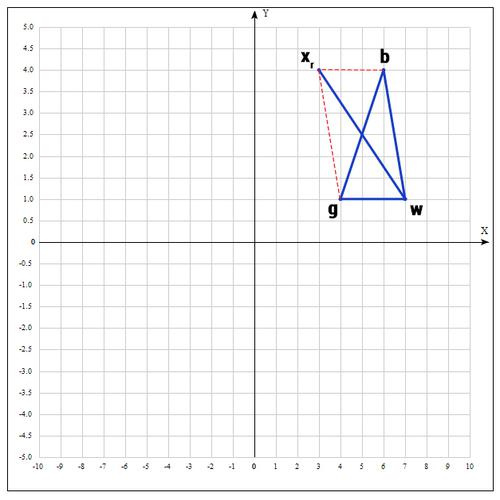
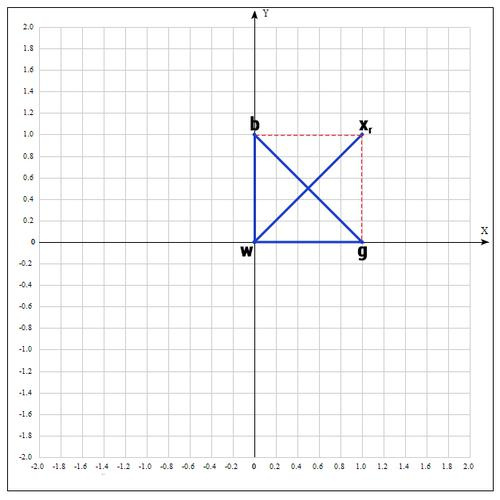
Находим точку (операция отражения):
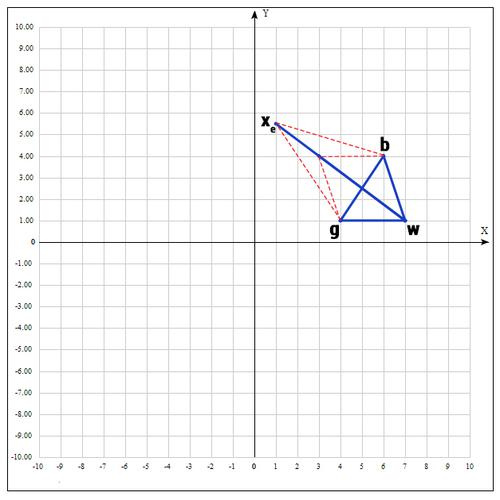
, т.к. пробуем увеличить отрезок (операция растяжения).
Проверяем значение функции в точке :
Оказалось, что точка «лучше» точки b. Следовательно мы получаем новые вершины:
И алгоритм начинается сначала.
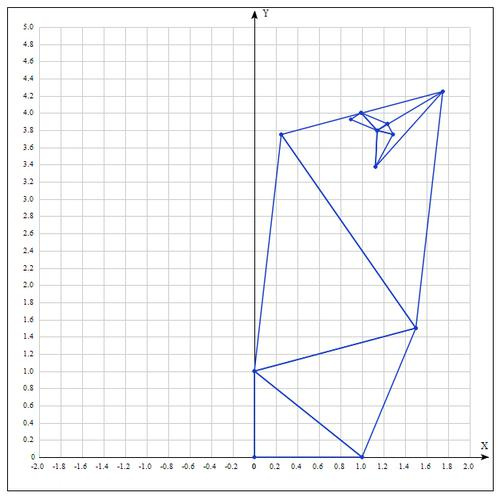
Таблица значений для 10 итераций:
| Best | Good | Worst |
|---|
Аналитически находим экстремум функции, он достигается в точке .
После 10 итераций мы получаем достаточно точное приближение:
Еще о методе:
Алгоритм Нелдера — Мида в основном используется для выбора параметра в машинном обучении. В сущности, симплекс-метод используется для оптимизации параметров модели. Это связано с тем, что данный метод оптимизирует целевую функцию довольно быстро и эффективно (особенно там, где не используется shrink — модификация).
С другой стороны, в силу отсутствия теории сходимости, на практике метод может приводить к неверному ответу даже на гладких (непрерывно дифференцируемых) функциях. Также возможна ситуация, когда рабочий симплекс находится далеко от оптимальной точки, а алгоритм производит большое число итераций, при этом мало изменяя значения функции. Эвристический метод решения этой проблемы заключается в запуске алгоритма несколько раз и ограничении числа итераций.
Реализация на языке программирования python:
Создаем вспомогательный класс Vector и перегружаем операторы для возможности производить с векторами базовые операции. Я намерено не использовал вспомогательные библиотеки для реализации алгоритма, т.к. в таком случае зачастую снижается восприятие.
#!/usr/bin/python # -*- coding: utf-8 -*- class Vector(object): def __init__(self, x, y): """ Create a vector, example: v = Vector(1,2) """ self.x = x self.y = y def __repr__(self): return "(, )".format(self.x, self.y) def __add__(self, other): x = self.x + other.x y = self.y + other.y return Vector(x, y) def __sub__(self, other): x = self.x - other.x y = self.y - other.y return Vector(x, y) def __rmul__(self, other): x = self.x * other y = self.y * other return Vector(x, y) def __truediv__(self, other): x = self.x / other y = self.y / other return Vector(x, y) def c(self): return (self.x, self.y) # objective function def f(point): x, y = point return x**2 + x*y + y**2 - 6*x - 9*y def nelder_mead(alpha=1, beta=0.5, gamma=2, maxiter=10): # initialization v1 = Vector(0, 0) v2 = Vector(1.0, 0) v3 = Vector(0, 1) for i in range(maxiter): adict = points = sorted(adict.items(), key=lambda x: x[1]) b = points[0][0] g = points[1][0] w = points[2][0] mid = (g + b)/2 # reflection xr = mid + alpha * (mid - w) if f(xr.c()) < f(g.c()): w = xr else: if f(xr.c()) < f(w.c()): w = xr c = (w + mid)/2 if f(c.c()) < f(w.c()): w = c if f(xr.c()) < f(b.c()): # expansion xe = mid + gamma * (xr - mid) if f(xe.c()) < f(xr.c()): w = xe else: w = xr if f(xr.c()) >f(g.c()): # contraction xc = mid + beta * (w - mid) if f(xc.c()) < f(w.c()): w = xc # update points v1 = w v2 = g v3 = b return b print("Result of Nelder-Mead algorithm: ") xk = nelder_mead() print("Best poits is: %s"%(xk)) Спасибо за чтение статьи. Надеюсь она была Вам полезна и Вы узнали много нового.
С вами был FUNNYDMAN. Удачной оптимизации!)