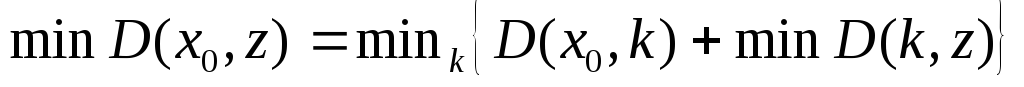Найти кратчайший путь путем динамического программирования

Вопрос 9. Основные понятия динамического программирования Задача о выборе кратчайшего пути .

Дан неориентированный граф, для каждого ребра которого задана его длина. Вершины графа пронумерованы числами от 1 до N. Требуется найти путь минимальной длины, соединяющий 1-ю вершину с N-й.

Решим эту задачу методом динамического программирования.

1. Инвариантное погружение.

Рассмотрим семейство задач P(k), k=1. N, где P(k) – задача о нахождении пути минимальной длины, соединяющий 1-ю вершину с k-й. Исходная задача запишется в виде P(N).

1. Функция Беллмана.

Пусть B(k) – длина минимального пути в задаче P(k), x*(k) – последовательность дуг оптимального пути в этой задаче.

1. Уравнение Беллмана (связь между решениями задач семейства).

Пусть G – множество вершин, для которых задача нахождения минимального пути уже решена. Рассмотрим множество вершин G₁, смежных с множеством G, т.е. не входящих в G, но в которые можно попасть из множества G по некоторой дуге графа. Обозначим l=(x,y) – дуга l начинается в вершине x и заканчивается в вершине y, d(l) – длина дуги l. Пусть min1, kG> = d(l*)+B(k*), l*=(m*,k*). (3.3.1) Тогда B(m*) = d(l*)+B(k*), (3.3.2) причем x*(m*) = (x*(k*), l*). (3.3.3)

1. Решение семейства задач

Уравнения (3.3.1) – (3.3.3) фактически не надо решать. Они указывают последовательность решения задач нашего семейства. Самые простая задача – найти кратчайший путь из 1-й вершины в эту же вершину, при этом B(1)=0, x*(1) не содержит дуг. Таким образом, первоначально множество G = , G₁ содержит все смежные с 1-й вершины. Уравнения (3.3.1)–(3.3.3) позволяют расширить множество G, вычислив значение B для одной из смежных вершин (для той, на которой достигается минимум в (3.3.1)). Пример. На рисунке 3.3.1 задан граф. 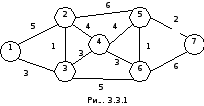Требуется найти кратчайший путь из вершины 1 в вершину 7. Решение. По принципу динамического программирования рассмотрим семейство задач P(k), состоящих в отыскании кратчайшего пути из вершины 1 в вершину k. Оптимальный путь x*(k) будем описывать упорядоченным множеством вершин, через которые он проходит. На первом этапе мы знаем решение только задачи P(1), для которой B(1)=0, x*(1)=. Результаты расчетов будем записывать в таблицу. Первый столбец будет содержать вершины из множества G, для которых есть смежные вершины из G₁. В ячейки этого столбца запишем номер вершины k и (в скобках) значение B(k), а также номер предпоследней вершины в оптимальном пути. Остальным столбцам будут соответствовать вершины из множества G₁ (смежные вершинам первого столбца). В каждой из ячеек (k,j) мы запишем сумму B(k)+d(k;j), где d(k;j) – длина дуги, соединяющей вершины k и j. Таблица 3.3.1

G1
G	2	3
1 (0, 1)	0+ 5=5	0+3=3

Минимум из значений ячеек, равный 3, достигается при k=1, j=3. Поэтому B(3) = 3, причем предпоследняя вершина в оптимальном пути имеет номер 1. Записываем таблицу для G= (если вершины k и j не соединяются дугой, ячейка остается пустой). Таблица 3.3.2

G1
G	2	4	6
1 (0, 1)	0+ 5=5
3 (3, 1)	3+1=4	3+3=6	3+5=8

Минимум из значений ячеек, равный 4, достигается при k=3, j=2. Поэтому B(2) = 4, предпоследняя вершина в оптимальном пути имеет номер 3. Записываем таблицу для G= (первую вершину мы далее не рассматриваем, т.к. она уже не связана дугами с вершинами из G₁). Таблица 3.3.3

G1
G	4	5	6
2 (4, 3)	4+4=8	4+6=10
3 (3, 1)	3+3=6	3+5=8

Минимум из значений ячеек, равный 6, достигается при k=3, j=4. B(4)=6, предпоследняя вершина в оптимальном пути имеет номер 3. Записываем таблицу для G=. Таблица 3.3.4

G1
G	5	6
2 (4, 3)	4+6=10
3 (3, 1)	3+5=8
4 (6, 3)	6+4=10	6+3=9

Минимум из значений ячеек, равный 8, достигается при k=3, j=6. B(6)=8, предпоследняя вершина в оптимальном пути имеет номер 3. Записываем таблицу для G= (вершина 3 далее не участвует). Таблица 3.3.5

G1
G	5	7
2 (4, 3)	4+6=10
4 (6, 3)	6+4=10
6 (8, 3)	6+4=10	6+6=12

Минимум из значений ячеек, равный 10, достигается при k=2, 4 и 6, j=5. B(5)=9, а предпоследней вершиной в оптимальном пути можно считать любую из вершин с номерами 2, 4 или 6. Записываем таблицу для G= (участвуют только вершины 5 и 6). Таблица 3.3.6

G1
G	7
5 (9, 2)	9+2=11
6 (8, 3)	6+6=12

B(7)=11, предпоследняя вершина – номер 5. В итоге вершина номер 7 попала в множество G, следовательно, расчеты заканчиваются. Таблица 3.3.7

G

1 (0, 1)

2 (4, 3)

3 (3, 1)

4 (6, 3)

5 (9, 2)

6 (8, 3)

7 (11,5)

Итак, длина минимального пути из 1 в 7 равна 11. Можно выписать и сам путь, т.е. оптимальный порядок прохождения вершин графа. По таблице 3.3.7 находим, что для вершины 7 предпоследняя вершина в оптимальном пути – вершина 5, для вершины 5 – вершина 2, для вершины 2 – вершина 3, для вершины 3 – вершина 1. Ответ: оптимальный путь: 1, 3, 2, 5, 7 имеет длину

Источник

Занятие 5. Решение задач ДП: Задача поиска кратчайшего пути (о поиске минимального расстояния)

Представим граф, представляющий собой воображаемую карту дорог, вершинами которого являются точки пересечения дорог или перекрестки (A11, A21, A31, A12, A22, A31, A13, A23…), см. рис. 5.1.

Необходимо добраться из дома на работу, сделать это следует за минимальное время или другими словами — с помощью маршрута минимальной длины.

Рис. 5.1. Граф для задачи поиска кратчайшего пути

Итак, наша цель:

1. определить путь минимальной длины;
2. определить минимальное расстояние от дома до работы.

Введем условные дополнения:

Как решить задачу без использования методов ДП?

Наивное решение

Наивным решением может быть метод перебора.

Граф имеет структуру — порядок слева направо.

• взять 1-й путь и найти его длину d1
• взять 2-й путь и найти его длину d2
• …
• взять k -й путь и найти его длину dk

После этого определить минимальный путь посредством процедуры argmin (d_i) , i=1. k

Т.е. решить такую задачу можно перебором.

Минус:
Посчитаем количество путей (из каждой вершины) — получим 18 путей.
Это не так мало, задача ведь простая.

При увеличении графа количество путей будет расти экспоненциально (путем умножения), как функция количества перекрестков.

Такие алгоритмы считаются не эффективными.

Другой вариант:
Можно воспользоваться так называемыми алгоритмами на графах, например, алгоритмом Дейкстра. О них поговорим на другой лекции.

Использование методов динамического программирования

Для начала обратим внимание, что у задачи есть структура — порядок вершин. Т.е. такой линейный порядок можно определить, как количество перекрестков, которые нужно миновать, доехав до работы.

Двигаясь от точки, обозначающей работу, разобьем граф на количество уровней перекрестков (рис. 5.2):

Рис. 5.2. Количество уровней перекрестков, которые надо пересечь, доехав до работы

Получилось 4 уровня перекрестков от Дома до Работы.

Этим порядком и воспользуемся для решения задачи поиска кратчайшего пути методом динамического программирования.

Предположим, что мы находимся на последнем уровне перекрестков от Работы.
На последнем уровне перекрестков минимальная длина пути из каждого перекрестка до работы известна (из таблицы) — это 4 и 3.

Зная минимальную длину пути из этого уровня перекрестков до Работы, можно ли найти минимальную дину пути из следующего уровня (A21, A22, A23) до Работы? — да можно. Например, из точки А21 нужно посмотреть всего два варианта: А21 -> A31 и A21 -> A32 . Затем выбрать минимальный из них, воспользовавшись процедурой argmin .

Теперь, зная минимальную длину пути из перекрестков второго уровня до Работы, можно найти минимальную длину пути из перекрестков третьего уровня до Работы.

И так и продолжим, пока не найдем минимальную длину пути от Дома до Работы.

Словесный алгоритм мы разработали. Теперь приступим к решению.

F_Aij — минимальная длина пути из перекрестка Aij до работы.
Запишем формулу. Начнем с последнего уровня перекрестков, двигаясь влево.

F_{3,j (j)=1,2} F_3,1 — минимальная длина пути из перекрестка A₃₁ до Работы = 4
F_3,2 — минимальная длина пути из перекрестка A₃₂ до Работы = 3

F_3,1 = 4
F_3,2 = 3

F_2,2 — это второй уровень, состоящий из перекрестков А₂₁, А₂₂, А₂₃

Рассмотрим перекресток А₂₂, из которого есть два пути:

А₂₂ argmin : 6 F_2,2 = min[A22 -> A31 -> Работа; A22 -> A32 -> Работа] = min[3 + 4; 3 + 3] = 6 (А_3,2)

Рассчитываем следующую ветвь второго уровня:

F_2,1 = min[A21 -> A31 -> Работа; A21 -> A32 -> Работа] = min(3 + 4; 2 + 3) = 5 (А₃₂)

Рассчитываем последнюю оставшуюся ветвь второго уровня:

Рассматриваем третий уровень перекрестков:

F_1,1 (перекресток A₁₁) = min[A11 -> A21 -> F_2,1;A11 -> A22 -> F_2,2;A11 -> A23 -> F_2,3] = min[2 + 5;1 + 6;1 + 5] = 6 (A₂₃) (А₃₁)

F_1,2 (перекресток A₁₂) = min[1 + 5;2 + 6;1 + 5] = 6 (A₂₃) (А₂₁), можно взять любой минмимум из двух

F_1,3 (перекресток A₁₃)= min[2 + 5;3 + 6;2 + 5] = 7 (A₂₃) (А₂₁), можно взять любой минмимум из двух

F3	F2	F1
1	4	5 (A32)	6 (A23)
2	3	6 (A32)	5 (A21)
—	—	5 (A31)	7 (A21)

Осталось найти цель — из Дома:

F_Дом = min[1 -> A11 -> F11; 2 -> A12 -> F12; 3 -> A13 -> F13] = min[1 + 6;2 + 6;3 + 7] = 7 (A₁₁)

Длина минимального пути из Дома до Работы = 7
Восстановим минимальный путь: A11 -> A23 -> A31 — > Работа

Сложность решения: решая задачу с перебором, приходилось умножать ( 3 * 3 * 2 ), а в данной задаче нам необходимо складывать. Т.е. мы получаем вместо экспоненциальной функции эффективное полеомиальное решения.

Но решение работает не для всех графов, например, если можно двигаться во всех направлениях, не только слева направо, то функция работать не будет.

Источник

10. Определение кратчайшего пути в сети методом динамического программирования

В рассматриваемой задаче граф имеет истоки сток, а каждая дуга имеет длину.

I.Вначале рассмотримсеть без циклов.

Требуется найти путь минимальной длины — последовательность смежных вершин с минимальной суммой длин соединяющих их дуг. Обозначимрасстояние между вершинами, положив при этоми, если.

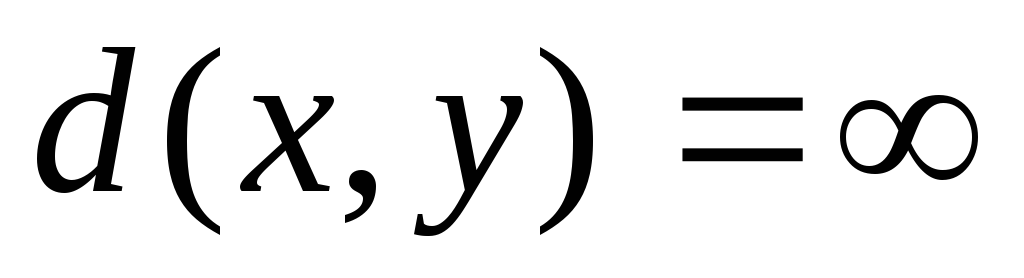
Метод динамического программирования основан на использовании соотношений Беллмана:

.

Алгоритм решения задачи предполагает просмотр и раскрытие всех вершин, начиная сконечнойвершины. Раскрытие означает присвоение вершинепометки следующего вида:, где— уже раскрытая смежнаяcвершина,— длина пути извкратчайшей длины,— длина дуги,— длина кратчайшего пути ихв.

Присвоить стоку пометку. Каждой нераскрытой вершине, смежной с, присвоить пометку, где

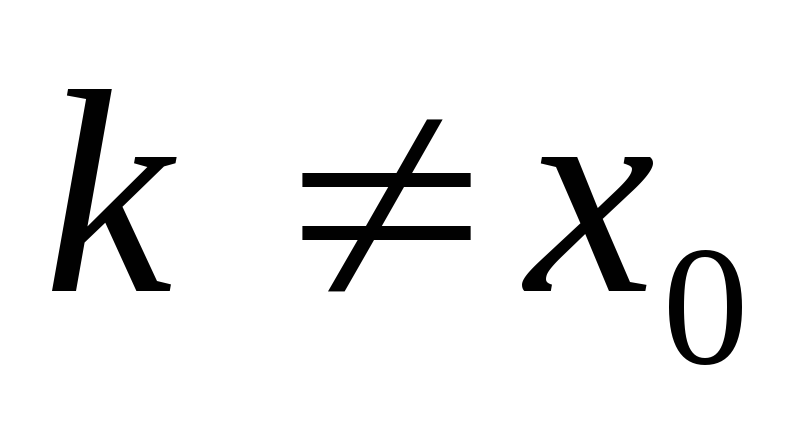
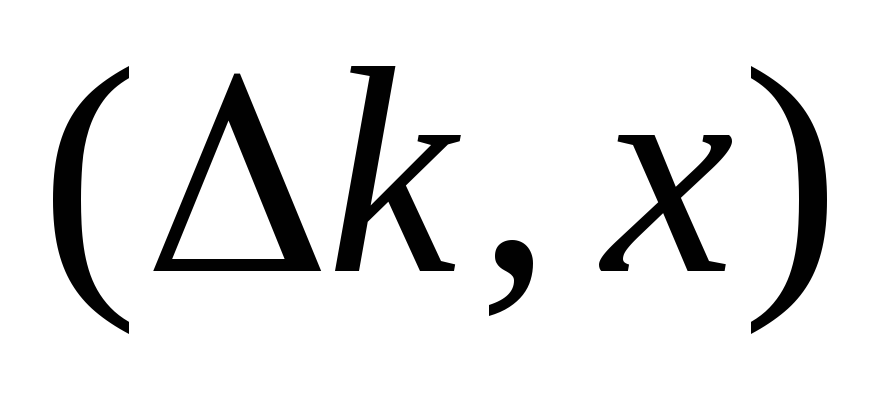
Если существует нераскрытая вершина , присвоить ей пометку.

Если исток раскрыт, то его пометка включает длину кратчайшего пути в сети и имя следующей зах₀ вершиной.

Обратный просмотр. Двигаясь по пометкам в направлении стока, получают последовательность вершин кратчайшего пути. Конец.

Замечания: 1) кратчайший путь может быть не единственным; 2) приведенный алгоритм применим для поиска самого длинного пути в сети.

Пример. Транспортная сеть задана на рисунке ориентированным графом (рис.10.1). Над дугами проставлены их длины. Считается, что дуги в обратном направлении имеют неограниченную длину.

Истоку присваивается пометка . Смежные с истоком вершины раскрываются следующим образом:, а вершинаc допускает три возможные пометки:

, причем лучшей, согласно соотношению Беллмана, является , т.к. кратчайший путь из с в z проходит через вершину d. Две другие пометки в дальнейшем не учитываются (исключаются). Аналогично раскрывают вершины a и b.

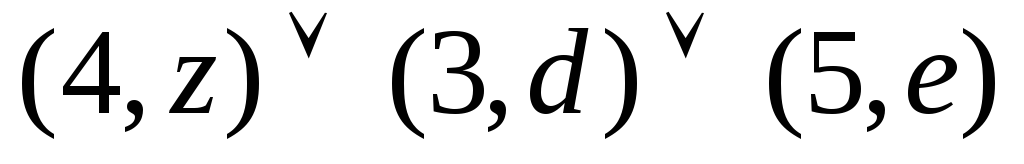
Наконец, исток может быть раскрыт тремя способами, причем две из трех пометок иявляются лучшими. Далее выполняется обратный просмотр, и по именам вершин в разметке восстанавливаются два пути минимальной длины:или. Кратчайшая длина пути равна 8.

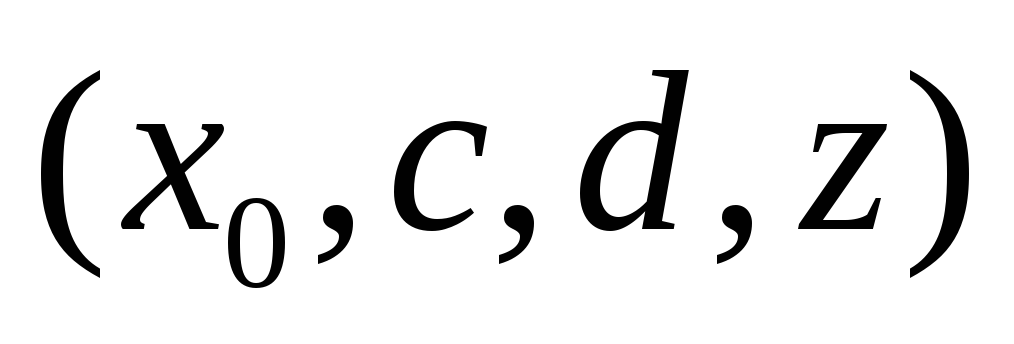
1. Сформулировать идею метода динамического программирования.

2. Выяснить возможность применимости метода для нахождения пути

Задание. Определить наименьший путь в заданной сети без циклов:

Длины дуг заданы таблицей:

Источник