Найти корень функции python

Как извлечь корень в Python

Квадратный корень из числа — это значение, которое при умножении само на себя дает исходное число. Каждое положительное число имеет два квадратных корня (то же значение с положительным и отрицательным знаками). Ниже приводится запись квадратного корня:
√25 = ±5

Для отрицательного числа результат извлечения квадратного корня включает комплексные числа, обсуждение которых выходит за рамки данной статьи.

Математическое представление квадрата числа

Все мы в детстве узнали, что, когда число умножается само на себя, мы получаем его квадрат. Также квадрат числа можно представить как многократное умножение этого числа. Попробуем разобраться в этом на примере.

Предположим, мы хотим получить квадрат 5. Если мы умножим число (в данном случае 5) на 5, мы получим квадрат этого числа. Для обозначения квадрата числа используется следующая запись:
5 2 = 25

При программировании на Python довольно часто возникает необходимость использовать функцию извлечения квадратного корня. Есть несколько способов найти квадратный корень числа в Python.

1. Используя оператор возведения в степень

 
num = 25 sqrt = num ** (0.5) print("Квадратный корень из числа "+str(num)+" это "+str(sqrt))
 
Квадратный корень из числа 25 это 5.0
 
Объяснение: Мы можем использовать оператор «**» в Python, чтобы получить квадратный корень. Любое число, возведенное в степень 0.5, дает нам квадратный корень из этого числа.
 
2. Использование math.sqrt()
 
Квадратный корень из числа можно получить с помощью функции sqrt() из модуля math , как показано ниже. Далее мы увидим три сценария, в которых передадим положительный, нулевой и отрицательный числовые аргументы в sqrt() .
 
a. Использование положительного числа в качестве аргумента.
 
 
import math num = 25 sqrt = math.sqrt(num) print("Квадратный корень из числа " + str(num) + " это " + str(sqrt))
 
Вывод: Квадратный корень из числа 25 это 5.0 .
 
b. Использование ноля в качестве аргумента.
 
 
import math num = 0 sqrt = math.sqrt(num) print("Квадратный корень из числа " + str(num) + " это " + str(sqrt))
 
Вывод: Квадратный корень из числа 0 это 0.0 .
 
c. Использование отрицательного числа в качестве аргумента.
 
 
import math num = -25 sqrt = math.sqrt(num) print("Квадратный корень из числа " + str(num) + " это " + str(sqrt))
 
Traceback (most recent call last): File "C:\wb.py", line 3, in sqrt = math.sqrt(num) ValueError: math domain error
 
Объяснение: Когда мы передаем отрицательное число в качестве аргумента, мы получаем следующую ошибку «math domain error». Из чего следует, что аргумент должен быть больше 0. Итак, чтобы решить эту проблему, мы должны использовать функцию sqrt() из модуля cmath .
 
3. Использование cmath.sqrt()
 
Ниже приведены примеры применения cmath.sqrt() .
 
а. Использование отрицательного числа в качестве аргумента.
 
Источник
 
Решение нелинейных уравнений#
 
Подмодуль scipy.optimize также содержит в себе методы для поиска корней нелинейных уравнений и их систем.
 
from matplotlib import pyplot as plt def configure_matplotlib(): plt.rc('text', usetex=True) plt.rcParams["axes.titlesize"] = 28 plt.rcParams["axes.labelsize"] = 24 plt.rcParams["legend.fontsize"] = 24 plt.rcParams["xtick.labelsize"] = plt.rcParams["ytick.labelsize"] = 18 plt.rcParams["text.latex.preamble"] = r""" \usepackage[utf8]  \usepackage[english,russian]  \usepackage  """ configure_matplotlib() 
 
Поиск корня скалярной функции одного аргумента#
 
Функция scipy.optimize.root_scalar позволяет искать корни функции \(f\colon \mathbb \to \mathbb\) :
 
Функция root_scalar предоставляет доступ к разным методам поиска корней, таким как newton , bisect , secant и многим другим. Какие-то из этих методов ищут корень внутри отрезка bracket , а другие ищут корень, начиная с какого-то начального приближения x0 .
 
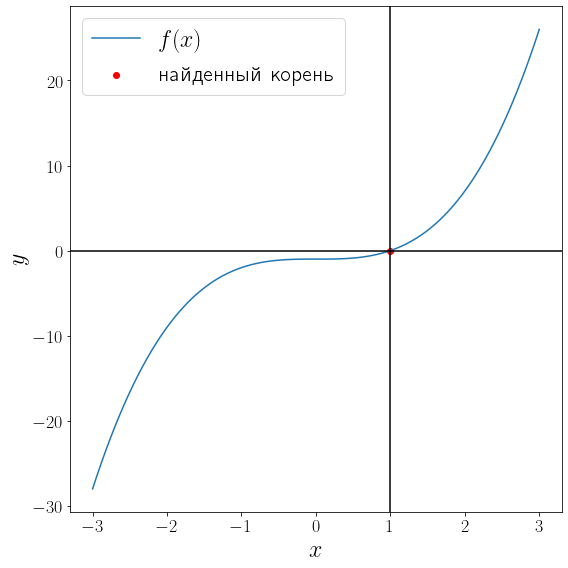
import numpy as np from scipy import optimize from matplotlib import pyplot as plt def f(x): return x**3 - 1 solution = optimize.root_scalar(f, bracket=[-10, 10], method="bisect") print(solution) x = np.linspace(-3, 3, 100) fig, ax = plt.subplots(figsize=(8, 8), layout="tight") ax.plot(x, f(x), label="$f(x)$") ax.scatter(solution.root, f(solution.root) , color="red", label="найденный корень") ax.axvline(solution.root, color="black") ax.axhline(0, color="black") ax.set_xlabel("$x$") ax.set_ylabel("$y$") ax.legend() 
 
converged: True flag: 'converged' function_calls: 46 iterations: 44 root: 1.0000000000002274
 
 
Метод бисекции сошелся за 44 итерации. Проверим метод Ньютона.
 
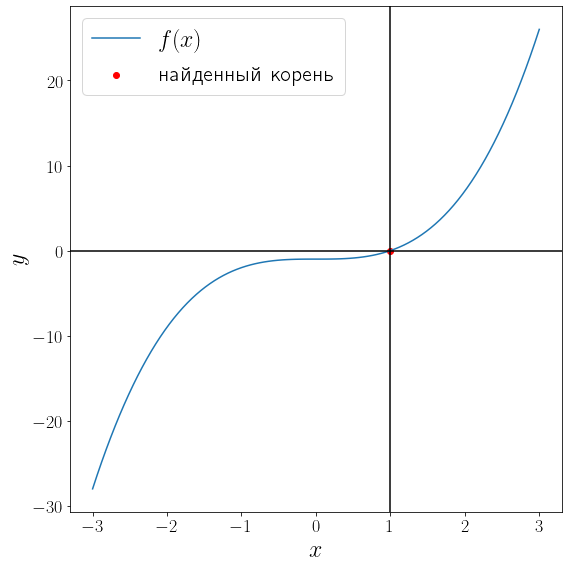
def fprime(x): return 3 * x**2 solution = optimize.root_scalar(f, fprime=fprime, x0=-2, method="newton") print(solution) fig, ax = plt.subplots(figsize=(8, 8), layout="tight") ax.plot(x, f(x), label="$f(x)$") ax.scatter(solution.root, f(solution.root) , color="red", label="найденный корень") ax.axvline(solution.root, color="black") ax.axhline(0, color="black") ax.set_xlabel("$x$") ax.set_ylabel("$y$") ax.legend() 
 
converged: True flag: 'converged' function_calls: 20 iterations: 10 root: 1.0
 
 
Метод Ньютона сошелся за 11 итераций.
 
Решение системы нелинейных уравнений.#
 
Функция optimize.root предназначена для поиска корней уравнений вида
 
где \(x\in\mathbb^n\) и \(F\colon \mathbb^n \to \mathbb^n\) многомерны, т.е. optimize.root решает системы вида
 
Рассмотрим поиск корня на примере функции
 
Матрица Якоби этого уравнения имеет вид
 
\[\begin \begin 1 + \frac(x_2 - x_1)^2 & \frac(x_2 - x_1)^2 \\ \frac(x_2 - x_1)^2 & 1 + \frac(x_2 - x_1)^2 \end, \end\]
 
а единственный действительный корень которой
 
В самом простом варианте достаточно передать методу optimize.root функцию левой части уравнения \(F\) и начальное приближение к корню.
 
import numpy as np from scipy import optimize from matplotlib import pyplot as plt def f(x): x = np.array(x) return np.array([ x[0] + 0.5 * (x[0] - x[1])**3 - 1.0, 0.5 * (x[1] - x[0])**3 + x[1] - 1.0 ]) solution = optimize.root(f, x0 = [0, 0]) print(solution) 
 
fjac: array([[-1.00000000e+00, -1.09073861e-12], [ 1.09073861e-12, -1.00000000e+00]]) fun: array([0., 0.]) message: 'The solution converged.' nfev: 5 qtf: array([-2.18114415e-12, -2.18114415e-12]) r: array([-1.00000000e+00, -2.18119967e-12, -1.00000000e+00]) status: 1 success: True x: array([1., 1.])
 
Если известно аналитическое выражение для производно, то лучше задействовать его и передать по параметру jac .
 
def jac(x): return np.array([ [1 + 1.5 * (x[0] - x[1])**2, -1.5 * (x[0] - x[1])**2], [-1.5 * (x[1] - x[0])**2, 1 + 1.5 * (x[1] - x[0])**2] ]) solution = optimize.root(f, jac=jac, x0 = [0, 0], method="hybr") print(solution) 
 
fjac: array([[-1., 0.], [ 0., -1.]]) fun: array([0., 0.]) message: 'The solution converged.' nfev: 2 njev: 1 qtf: array([1., 1.]) r: array([-1., -0., -1.]) status: 1 success: True x: array([1., 1.])
 
Источник
 
Как найти положительный корень заданной функции?
 
"написать программу, которая находит положительный корень функции f(x)=x^2-5 c погрешность =10^-6" 
ваще в питоне разобраться толком не могу от паскаля он далек, кто, что то понимает подскажите плиз как делать))
 
 
 Найти наименьший положительный корень уравнения, первую и вторую производную функции. Фото с заданием внутри
Вот условия, выручайте форумчане, до 19:45 сдать, пока препод добрый 🙂 Заранее спасибо.
 
Вычислить наименьший положительный ненулевой корень уравнения с заданной точностью
С точностью 10-5 вычислить наименьший положительный ненулевой корень уравнения tg x = 2x .
 
 
 Найти с заданной точностью корень функции
написать программы, реализующие рекурсивный и итерационный метод решения задач. найти с заданной.
 
 
 Найти корень заданной функции (метод дихотомии)
Нужно найти корень заданной функции в пределах заданного пользователем диапазона методом дихотомии.
 
 
 Найти корень Функции на заданном промежутке с заданной точностью
Найти корень Функции на заданном промежутке , с точностью, двумя способами. Первый способ.
 
Источник
 
Читайте также:  Сменить версию php htaccess