Наибольший общий делитель алгоритм питон

Нахождение НОК и НОД в Python — примеры

В данном уроке мы узнаем, как найти наименьшее общее кратное (НОК) и наибольший общий делитель (НОД) с помощью языка программирования Python.

Но прежде чем мы начнем, давайте разберем, что обозначает Least Common Multiple (LCM) — наименьшее общее кратное.

НОК: наименьшее общее кратное

Это понятие арифметики и системы счисления. НОК двух целых чисел a и b обозначается НОК(a,b). Это наименьшее натуральное число, которое делится и на «а», и на «b».

Например: у нас есть два целых числа 4 и 6. Найдем НОК:

4, 8, 12, 16, 20, 24, 28, 32, 36. and so on.

6, 12, 18, 24, 30, 36, 42. and so on.

Общие кратные 4 и 6 — это просто числа, которые есть в обоих списках:

12, 24, 36, 48, 60, 72. and so on.

НОК — это наименьший общий множитель, поэтому он равен 12.

Поскольку мы поняли основную концепцию НОК, давайте рассмотрим следующую программу для нахождения НОК заданных целых чисел.

# defining a function to calculate LCM def calculate_lcm(x, y): # selecting the greater number if x > y: greater = x else: greater = y while(True): if((greater % x == 0) and(greater % y == 0)): lcm = greater break greater += 1 return lcm # taking input from users num1 = int(input("Enter first number: ")) num2 = int(input("Enter second number: ")) # printing the result for the users print("The L.C.M. of", num1,"and", num2,"is", calculate_lcm(num1, num2))

Enter first number: 3 Enter second number: 4 The L.C.M. of 3 and 4 is 12

Эта программа сохраняет два числа в num1 и num2 соответственно. Эти числа передаются в функцию calculate_lcm(). Функция возвращает НОК двух чисел.

Внутри функции мы сначала определили большее из двух чисел, поскольку наименьшее общее кратное может быть больше или равно наибольшему числу. Затем мы используем бесконечный цикл while, чтобы перейти от этого числа и дальше.

На каждой итерации мы проверяли, идеально ли делят оба числа число. Если это так, мы сохранили число как НОК и вышли из цикла. В противном случае число увеличивается на 1, и цикл продолжается.

НОД: наибольший общий делитель

В этом разделе мы разберем, как найти Highest Common Factor (HCF) — наибольший общий делитель (НОД) в языке программирования Python.

Наибольший общий делитель двух или более целых чисел, когда хотя бы одно из них не равно нулю, является наибольшим положительным целым числом, которое без остатка делит целые числа. Например, НОД 8 и 12 равен 4.

У нас есть два целых числа 8 и 12. Найдем наибольший общий делитель.

Теперь давайте рассмотрим пример, основанный на нахождении НОД двух заданных чисел.

# defining a function to calculate HCF def calculate_hcf(x, y): # selecting the smaller number if x > y: smaller = y else: smaller = x for i in range(1,smaller + 1): if((x % i == 0) and(y % i == 0)): hcf = i return hcf # taking input from users num1 = int(input("Enter first number: ")) num2 = int(input("Enter second number: ")) # printing the result for the users print("The H.C.F. of", num1,"and", num2,"is", calculate_hcf(num1, num2))

Enter first number: 8 Enter second number: 12 The H.C.F. of 8 and 12 is 4

В приведенном выше фрагменте кода два целых числа, хранящиеся в переменных num1 и num2, передаются в функцию calculate_hcf(). Функция вычисляет НОД для этих двух чисел и возвращает его.

Внутри функции мы должны определить меньшее число, поскольку НОД может быть меньше или равен наименьшему числу. Затем мы использовали цикл for, чтобы перейти от 1 к этому числу.

На каждой итерации мы должны проверять, точно ли число делит оба входных числа. Если это так, мы должны сохранить число как НОД. По завершении цикла мы получаем наибольшее число, которое идеально делит оба числа.

Источник

Как найти НОД двух чисел в Python – 4 способа

НОД – это математический термин, обозначающий наибольший общий делитель, который может идеально разделить два числа. НОД также известен как наибольший общий фактор(HCF).

Например, HCF / GCD двух чисел 54 и 24 равен 6. Поскольку 6 – это наибольший общий делитель, который полностью делит 54 и 24.

Разберемся как найти НОД двух чисел в Python.

НОД с использованием функции gcd()

gcd() в python – это встроенная функция, предлагаемая математическим модулем для поиска наибольшего общего делителя двух чисел.

Где a и b – два целых числа, которые передаются в качестве аргумента функции gcd().

Давайте создадим программу для печати НОД двух чисел, используя встроенную функцию math.gcd() в python.

# create a program to print the gcd of two number in python using the math.gcd() function. import math print(" GCD of two number 0 and 0 is ", math.gcd(0, 0)) #math.gcd(a, b), a and b are the two integer number print(" GCD of two number 0 and 48 is ", math.gcd(0, 48)) a = 60 # assign the number to variable a b = 48 # assign the number to variable b print(" GCD of two number 60 and 48 is ", math.gcd(a, b)) # pass the variable a and b to math.gcd() function. print(" GCD of two number 48 and -12 is ", math.gcd(48, -12)) # pass the integer number print(" GCD of two number -24 and -18 is ", math.gcd(-24, -18)) print(" GCD of two number -60 and 48 is ", math.gcd(-60, 48))

В приведенном выше примере функция math.gcd() генерирует НОД двух заданных чисел. В функции gcd() a и b передаются в качестве аргумента, который возвращает наибольший общий делитель двух целых чисел, полностью разделяя числа.

НОД с использованием рекурсии

Рекурсия – это функция, потребляющая память, определенная в Python, которая вызывает себя через самореферентное выражение. Это означает, что функция будет постоянно вызывать и повторять себя до тех пор, пока не будет выполнено определенное условие для возврата наибольшего общего делителя числа.

Псевдокод алгоритма

Шаг 1: Возьмите два входа, x и y, от пользователя.

Шаг 2: Передайте входной номер в качестве аргумента рекурсивной функции.

Шаг 3: Если второе число равно нулю(0), возвращается первое число.

Шаг 4: В противном случае он рекурсивно вызывает функцию со вторым числом в качестве аргумента, пока не получит остаток, который делит второе число на первое число.

Шаг 5: Вызовите или назначьте gcd_fun() переменной.

Шаг 6: Отобразите НОД двух чисел.

Шаг 7: Выйдите из программы.

Разберемся с программой для нахождения НОД двух чисел с помощью рекурсии.

# write a program to understand the GCD of two number in python using the recursion. def gcd_fun(x, y): if(y == 0): # it divide every number return x # return x else: return gcd_fun(y, x % y) x =int(input("Enter the first number: ")) # take first no. y =int(input("Enter the second number: ")) # take second no. num = gcd_fun(x, y) # call the gcd_fun() to find the result print("GCD of two number is: ") print(num) # call num

Нахождение НОД с помощью цикла

Давайте создадим программу для нахождения НОД двух чисел в Python с помощью циклов.

def GCD_Loop( a, b): if a > b: # define the if condition temp = b else: temp = a for i in range(1, temp + 1): if(( a % i == 0) and(b % i == 0 )): gcd = i return gcd x = int(input(" Enter the first number: ") ) # take first no. y =int(input(" Enter the second number: ")) # take second no. num = GCD_Loop(x, y) # call the gcd_fun() to find the result print("GCD of two number is: ") print(num) # call num

Как мы видим в приведенной выше программе, мы берем два значения в качестве входных и передаем эти числа в функцию GCD_Loop(), чтобы вернуть GCD.

Алгоритм Евклида

Алгоритм Евклида – эффективный метод нахождения наибольшего общего делителя двух чисел. Это самый старый алгоритм, который делит большее число на меньшее и берет остаток. Опять же, он делит меньшее число от остатка, и этот алгоритм непрерывно делит число, пока остаток не станет 0.

Например, предположим, что мы хотим вычислить HCF двух чисел, 60 и 48. Затем мы делим 60 на 48; он возвращает остаток 12. Теперь мы снова делим число 24 на 12, а затем он возвращает остаток 0. Таким образом, мы получаем HCF равным 12.

Псевдокод алгоритма Евклида

Шаг 1: Есть два целых числа, например a и b.

Шаг 2: Если a = 0, то НОД(a, b) равен b.

Шаг 3: Если b = 0, НОД(a, b) равен a.

Шаг 5: Предположим, что a = b и b = R.

Шаг 6: Повторяйте шаги 4 и 3, пока mod b не станет равным или большим 0.

Шаг 7: GCD = b и затем распечатайте результат.

Шаг 8: Остановите программу.

Найдем HCF или GCD двух чисел, используя алгоритм Евклида в python.

# Create a program to find the GCD of two number in python using the Euclid's Algorithm. def find_hcf(a,b): while(b): a, a = b, a % b return a a = int(input(" Enter the first number: ") ) # take first no. b = int(input(" Enter the second number: ")) # take second no. num = find_hcf(a, b) # call the find_hcf() to get the result print(" The HCF of two number a and b is ") print(num) # call num

Источник

Алгоритм Евклида — нахождение наибольшего общего делителя

Алгоритм Евклида – это алгоритм нахождения наибольшего общего делителя (НОД) пары целых чисел.

Наибольший общий делитель (НОД) – это число, которое делит без остатка два числа и делится само без остатка на любой другой делитель данных двух чисел. Проще говоря, это самое большое число, на которое можно без остатка разделить два числа, для которых ищется НОД.

Решение задачи на языке программирования Python

Алгоритм нахождения НОД делением

1. Большее число делим на меньшее.
2. Если делится без остатка, то меньшее число и есть НОД (следует выйти из цикла).
3. Если есть остаток, то большее число заменяем на остаток от деления.
4. Переходим к пункту 1.

Пример:
Найти НОД для 30 и 18.
30 / 18 = 1 (остаток 12)
18 / 12 = 1 (остаток 6)
12 / 6 = 2 (остаток 0)
Конец: НОД – это делитель 6.
НОД (30, 18) = 6

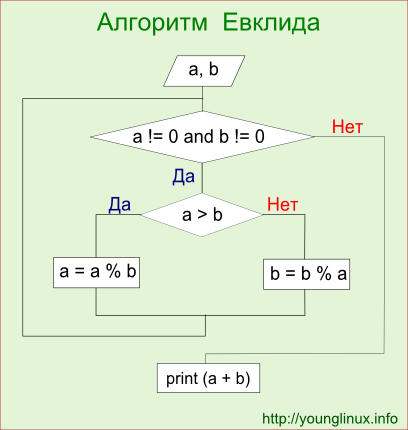
a = int(input()) b = int(input()) while a != 0 and b != 0: if a > b: a = a % b else: b = b % a print(a + b)

В цикле в переменную a или b записывается остаток от деления. Цикл завершается, когда хотя бы одна из переменных равна нулю. Это значит, что другая содержит НОД. Однако какая именно, мы не знаем. Поэтому для определения НОД находим сумму этих переменных. Поскольку в одной из переменных ноль, он не оказывает влияние на результат.

Если условием завершения цикла является равенство хотя бы одной из переменных нулю ( a == 0 or b == 0 ), то условием продолжения его работы является обратное этому условие — обе переменные должны иметь отличные от нуля значения ( a != 0 and b != 0 ).

Для того, чтобы вышеприведенная программа могла обрабатывать отрицательные числа, в логическом выражении при if должны сравниваться модули значений переменных: if abs ( a ) > abs ( b ) : . Иначе большим числом может оказаться меньшее по модулю. В этом случае интерпретатор Питона в качестве остатка от деления выдает вещественное число. В результате это приводит к зацикливанию, так как низвести переменные до нуля становится как минимум маловероятным.

Алгоритм нахождения НОД вычитанием

1. Из большего числа вычитаем меньшее.
2. Если получается 0, значит, числа равны друг другу и являются НОД (следует выйти из цикла).
3. Если результат вычитания не равен 0, то большее число заменяем на результат вычитания.
4. Переходим к пункту 1.

Пример:
Найти НОД для 30 и 18.
30 — 18 = 12
18 — 12 = 6
12 — 6 = 6
6 — 6 = 0
Конец: НОД – это уменьшаемое или вычитаемое.
НОД (30, 18) = 6

a = int(input()) b = int(input()) while a != b: if a > b: a = a - b else: b = b - a print(a)

Функция, вычисляющая НОД

def gcd(m, n): while m != n: if m > n: m = m - n else: n = n - m return n a = int(input()) b = int(input()) print(gcd(a, b))

Функция gcd модуля math

В модуле math языка программирования Python есть функция gcd , вычисляющая наибольший общий делитель двух чисел.

>>> import math >>> math.gcd(30, 18) 6

Источник