Multivariate linear regression python

Multivariate Linear Regression in Python with scikit-learn Library

In this post, we will provide an example of machine learning regression algorithm using the multivariate linear regression in Python from scikit-learn library in Python. The example contains the following steps:

Step 1: Import libraries and load the data into the environment.

Step 2: Generate the features of the model that are related with some measure of volatility, price and volume.

Step 3: Visualize the correlation between the features and target variable with scatterplots.

Step 4: Create the train and test dataset and fit the model using the linear regression algorithm.

Step 5: Make predictions, obtain the performance of the model, and plot the results.

Step 1: Import libraries and load the data into the environment.

We will first import the required libraries in our Python environment.

import pandas as pd from datetime import datetime import numpy as np from sklearn.linear_model import LinearRegression import matplotlib.pyplot as plt 

We will work with SPY data between dates 2010-01-04 to 2015-12-07.

First we use the read_csv() method to load the csv file into the environment. Make sure to update the file path to your directory structure.

SPY_data = pd.read_csv("C:/Users/FT/Documents/MachineLearningCourse/SPY_regression.csv") # Change the Date column from object to datetime object SPY_data["Date"] = pd.to_datetime(SPY_data["Date"]) # Preview the data SPY_data.head(10) 

The data has the following structure:

 Date Open High Low Close Volume Adj Close 0 2015-12-07 2090.419922 2090.419922 2066.780029 2077.070068 4.043820e+09 2077.070068 1 2015-12-04 2051.239990 2093.840088 2051.239990 2091.689941 4.214910e+09 2091.689941 2 2015-12-03 2080.709961 2085.000000 2042.349976 2049.620117 4.306490e+09 2049.620117 3 2015-12-02 2101.709961 2104.270020 2077.110107 2079.510010 3.950640e+09 2079.510010 4 2015-12-01 2082.929932 2103.370117 2082.929932 2102.629883 3.712120e+09 2102.629883 5 2015-11-30 2090.949951 2093.810059 2080.409912 2080.409912 4.245030e+09 2080.409912 6 2015-11-27 2088.820068 2093.290039 2084.129883 2090.110107 1.466840e+09 2090.110107 7 2015-11-25 2089.300049 2093.000000 2086.300049 2088.870117 2.852940e+09 2088.870117 8 2015-11-24 2084.419922 2094.120117 2070.290039 2089.139893 3.884930e+09 2089.139893 9 2015-11-23 2089.409912 2095.610107 2081.389893 2086.590088 3.587980e+09 2086.590088 

Let’s now set the Date as index and reverse the order of the dataframe in order to have oldest values at top.

# Set Date as index SPY_data.set_index('Date',inplace=True) # Reverse the order of the dataframe in order to have oldest values at top SPY_data.sort_values('Date',ascending=True) 

Step 2: Generate features of the model

We will generate the following features of the model:

• High — Low percent change
• 5 periods Exponential Moving Average
• Standard deviation of the price over the past 5 days
• Daily volume percent change
• Average volume for the past 5 days
• Volume over close price ratio

SPY_data['High-Low_pct'] = (SPY_data['High'] - SPY_data['Low']).pct_change() SPY_data['ewm_5'] = SPY_data["Close"].ewm(span=5).mean().shift(periods=1) SPY_data['price_std_5'] = SPY_data["Close"].rolling(center=False,window= 30).std().shift(periods=1) SPY_data['volume Change'] = SPY_data['Volume'].pct_change() SPY_data['volume_avg_5'] = SPY_data["Volume"].rolling(center=False,window=5).mean().shift(periods=1) SPY_data['volume Close'] = SPY_data["Volume"].rolling(center=False,window=5).std().shift(periods=1) 

Step 3: Visualize the correlation between the features and target variable

Before training the dataset, we will make some plots to observe the correlations between the features and the target variable.

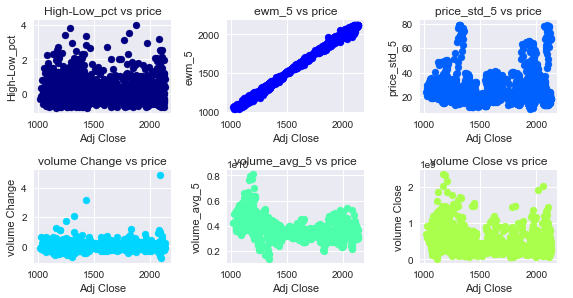
jet= plt.get_cmap('jet') colors = iter(jet(np.linspace(0,1,10))) def correlation(df,variables, n_rows, n_cols): fig = plt.figure(figsize=(8,6)) #fig = plt.figure(figsize=(14,9)) for i, var in enumerate(variables): ax = fig.add_subplot(n_rows,n_cols,i+1) asset = df.loc[:,var] ax.scatter(df["Adj Close"], asset, c = next(colors)) ax.set_xlabel("Adj Close") ax.set_ylabel("<>".format(var)) ax.set_title(var +" vs price") fig.tight_layout() plt.show() # Take the name of the last 6 columns of the SPY_data which are the model features variables = SPY_data.columns[-6:] correlation(SPY_data,variables,3,3) 

Correlations between Features and Target Variable (Adj Close)

The correlation matrix between the features and the target variable has the following values:

SPY_data.corr()['Adj Close'].loc[variables] High-Low_pct -0.010328 ewm_5 0.998513 price_std_5 0.100524 volume Change -0.005446 volume_avg_5 -0.485734 volume Close -0.241898 

Either the scatterplot or the correlation matrix reflects that the Exponential Moving Average for 5 periods is very highly correlated with the Adj Close variable. Secondly is possible to observe a negative correlation between Adj Close and the volume average for 5 days and with the volume to Close ratio.

Step 4: Train the Dataset and Fit the model

Due to the feature calculation, the SPY _ data contains some NaN values that correspond to the first’s rows of the exponential and moving average columns. We will see how many Nan values there are in each column and then remove these rows.

SPY_data.isnull().sum().loc[variables] High-Low_pct 1 ewm_5 1 price_std_5 30 volume Change 1 volume_avg_5 5 volume Close 5 # To train the model is necessary to drop any missing value in the dataset. SPY_data = SPY_data.dropna(axis=0) # Generate the train and test sets train = SPY_data[SPY_data.index < datetime(year=2015, month=1, day=1)] test = SPY_data[SPY_data.index >= datetime(year=2015, month=1, day=1)] dates = test.index 

Step 5: Make predictions, obtain the performance of the model, and plot the results

In this step, we will fit the model with the LinearRegression classifier. We are trying to predict the Adj Close value of the Standard and Poor’s index. # So the target of the model is the «Adj Close» Column.

lr = LinearRegression() X_train = train[["High-Low_pct","ewm_5","price_std_5","volume_avg_5","volume Change","volume Close"]] Y_train = train["Adj Close"] lr.fit(X_train,Y_train) 

Create the test features dataset ( X_test ) which will be used to make the predictions.

# Create the test features dataset (X_test) which will be used to make the predictions. X_test = test[["High-Low_pct","ewm_5","price_std_5","volume_avg_5","volume Change","volume Close"]].values # The labels of the model Y_test = test["Adj Close"].values 

Predict the Adj Close values using the X_test dataframe and Compute the Mean Squared Error between the predictions and the real observations.

close_predictions = lr.predict(X_test) mae = sum(abs(close_predictions - test["Adj Close"].values)) / test.shape[0] print(mae) 18.0904 

We have that the Mean Absolute Error of the model is 18.0904. This metric is more intuitive than others such as the Mean Squared Error, in terms of how close the predictions were to the real price.

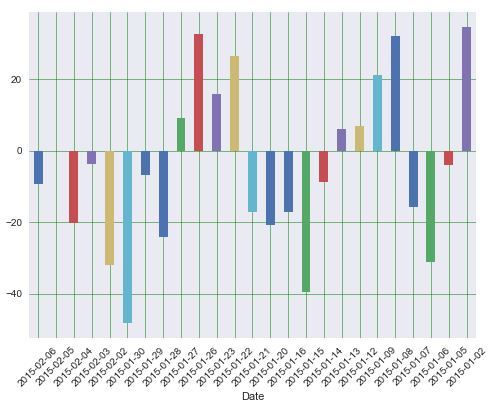
Finally we will plot the error term for the last 25 days of the test dataset. This allows observing how long is the error term in each of the days, and asses the performance of the model by date.

# Create a dataframe that output the Date, the Actual and the predicted values df = pd.DataFrame() df1 = df.tail(25) # set the date with string format for plotting df1['Date'] = df1['Date'].dt.strftime('%Y-%m-%d') df1.set_index('Date',inplace=True) error = df1['Actual'] - df1['Predicted'] # Plot the error term between the actual and predicted values for the last 25 days error.plot(kind='bar',figsize=(8,6)) plt.grid(which='major', linestyle='-', linewidth='0.5', color='green') plt.grid(which='minor', linestyle=':', linewidth='0.5', color='black') plt.xticks(rotation=45) plt.show() 

This concludes our example of Multivariate Linear Regression in Python.

Источник

Saved searches

Use saved searches to filter your results more quickly

You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. Reload to refresh your session. You switched accounts on another tab or window. Reload to refresh your session.

Implementation of multivariate linear regression using gradient descent in python

drbilo/multivariate-linear-regression

This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.

Name already in use

A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?

Sign In Required

Please sign in to use Codespaces.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching Xcode

If nothing happens, download Xcode and try again.

Launching Visual Studio Code

Your codespace will open once ready.

There was a problem preparing your codespace, please try again.

Latest commit

Git stats

Files

Failed to load latest commit information.

README.md

Multivariate Linear Regression w. Gradient Descent

Last time I talked about Simple Linear Regression which is when we predict a y value given a single feature variable x. However data is rarely that simple and we often can have many variables we can use. For example, what if we want to predict the cost of a house and we have access to the size, number of bedrooms, number of bathrooms, age etc. For this kind of prediction we need to use Multivariate Linear Regression.

Updated Hypothesis Function

Luckily to do this it doesn’t require too much to change compared to Simple Linear Regression. The updated hyptohesis function looks like so:

To calculate this efficiently, we can use matrix multiplication which is used in Linear Algebra. Using this method our hypothesis function looks like this:

To do this succesfully, we have to match our two matricies in size so that we can perform matrix multiplication. We acheive this by setting our first feature value . To explain more simply, the amount of columns in our training matrix must match the amount of rows in our theta vector.

The cost function remains similar to the one used in simple linear regression althogh an updated one using matrix operations looks like this:

This is implemented in my code as:

def cost_function(X, y, theta): m = y.size error = np.dot(X, theta.T) - y cost = 1/(2*m) * np.dot(error.T, error) return cost, error

For gradient descent to work with multiple features, we have to do the same as in simple linear regression and update our theta values simultaneously over the amount of iterations and using the learning rate we supply.

This is implemented in my code as:

def gradient_descent(X, y, theta, alpha, iters): cost_array = np.zeros(iters) m = y.size for i in range(iters): cost, error = cost_function(X, y, theta) theta = theta - (alpha * (1/m) * np.dot(X.T, error)) cost_array[i] = cost return theta, cost_array

This code also populltes a Numpy array of cost values so that we can plot a graph which shows the hopeful reduction in cost values as gradient descent runs.

A quick note on Feature Normalization

When working with multiple feature variables it will speed up gradient descent signicantly if they all are within a small range. We can achieve this using feature normalization. While there are a few ways to acheive this, a common used method uses the following method:

(The feature minus the mean of all the feature variables divided by the standard deviation)

To implement this version of linear regression I decided to use a 2 feature hyptohetical dataset that featured the size of a house and how many bedrooms it had. The y value would be the price.

Size	Bedrooms	Price
2104	3	399900
1600	3	329900
2400	3	369000
1416	2	232000

With theta values set to 0, the cost value returned the following amount:

With initial theta values of [0. 0. 0.], cost error is 65591548106.45744

After running gradient descent over the data, we see the cost value dropping:

After running for 2000 iterations (this value could be a lot smaller as convergence is acheived much earlier), gradient descent returns the following theta values:

With final theta values of [340397.96353532 109848.00846026 -5866.45408497], cost error is 2043544218.7812893

Источник