Molecular dynamics on python

Saved searches

Use saved searches to filter your results more quickly

You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. Reload to refresh your session. You switched accounts on another tab or window. Reload to refresh your session.

Molecular dynamics in Python

evenmn/mdlj-python

This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.

Name already in use

A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?

Sign In Required

Please sign in to use Codespaces.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching Xcode

If nothing happens, download Xcode and try again.

Launching Visual Studio Code

Your codespace will open once ready.

There was a problem preparing your codespace, please try again.

Latest commit

Git stats

Files

Failed to load latest commit information.

README.md

Molecular dynamics solver with the Lennard-Jones potential written in object-oriented Python for teaching purposes. The solver supports various integrators, boundary condition and initialization methods. However, it is simple as it only supports the Lennard-Jones potential and the microcanonical ensemble (NVE). Also, it only supports symmetric systems, i.e., all sides have the same length and take the same boundary conditions. Albeit efforts are put in making the code fast (mostly by replacing loops by vectorized operations), the performance cannot compete with packages written in low-level languages.

First download the contents:

$ git clone https://github.com/evenmn/mdlj-python

and then install the mdsolver:

$ cd mdlj-python $ pip install .

Example: Two oscillating particles in one dimension

A simple example where two particles interact with periodic motion can be implemented like this:

from mdsolver import MDSolver from mdsolver.initposition import SetPosition solver = MDSolver(position=SetPosition([[0.0], [1.5]]), dt=0.01) solver.thermo(1, "log.mdsolver", "step", "time", "poteng", "kineng") solver.run(steps=1000)

Example: 864 particles in three dimensions with PBC

A more complex example where 6x6x6x4=864 particles in three dimensions interact and where the boundaries are periodic is shown below. The particles are initialized in a face-centered cube, and the initial temperature is 300K (2.5 in Lennard-Jones units). We first perform an equilibration run, and then a production run.

from mdsolver import MDSolver from mdsolver.initposition import FCC from mdsolver.initvelocity import Temperature from mdsolver.boundary import Periodic solver = MDSolver(position=FCC(cells=6, lenbulk=10.2), velocity=Temperature(T=2.5), boundary=Periodic(lenbox=10.2), dt=0.01) # equilibration run solver.thermo(10, "equilibration.log", "step", "time") solver.run(steps=1000) solver.snapshot("after_equi.xyz") # production run solver.dump(1, "864N_3D.xyz", "x", "y", "z") solver.thermo(1, "production.log", "step", "time", "temp", "poteng", "kineng") solver.run(steps=1000, out="log") solver.snapshot("final.xyz")

The thermo style outputs (temperature, energy etc. ) are stored in a log file, rather than in arrays. This has two purposes: Storing thermo style outputs in arrays might be memory intensive, and the file can be kept for later simulations. Reading these log files (here production.log ) can easily be done using the Log-class:

from mdsolver.analyze import Log logobj = Log("production.log") time = logobj.find("time") temp = logobj.find("temp")

The find -method outputs a numpy array.

For more examples, see the examples folder.

Источник

Molecular Dynamics

We have introduced the classical potential models, and have derived and showen some of their basic properties. Now we can use these potential models to look at the dynamics of the system.

Force and acceleration

The particles that we study are classical in nature, therefore we can apply classical mechanics to rationalise their dynamic behaviour. For this the starting point is Newton’s second law of motion,

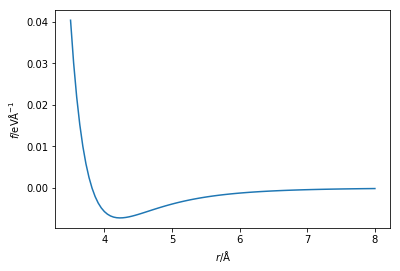
Which is to say that the force is the negative of the first derivative of the energy with respect to the postion of the particles. The Python code below creates a new function that is capable of calculating the force from the Lennard-Jones potential. The force on the atoms is then plotted.

%matplotlib inline import numpy as np import matplotlib.pyplot as plt def lj_force(r, epsilon, sigma): """ Implementation of the Lennard-Jones potential to calculate the force of the interaction. Parameters ---------- r: float Distance between two particles (Å) epsilon: float Potential energy at the equilibrium bond length (eV) sigma: float Distance at which the potential energy is zero (Å) Returns ------- float Force of the van der Waals interaction (eV/Å) """ return 48 * epsilon * np.power( sigma, 12) / np.power( r, 13) - 24 * epsilon * np.power( sigma, 6) / np.power(r, 7) r = np.linspace(3.5, 8, 100) plt.plot(r, lj_force(r, 0.0103, 3.4)) plt.xlabel(r'$r$/Å') plt.ylabel(r'$f$/eVÅ$^$') plt.show() 

You may have noticed that in Newton’s second law of motion, the force is a vector quantity, whereas the first negative derivative of the energy is a scalar. Therefore, it is important that we determine the force in each direction for our simulation. This is achieved by multiplication by the unit vector in that direction,

In the above equation, $r_x$ is the distance between the two particles in the $x$-dimension and $|\mathbf|$ is the magnitude of the distance vector. For simplicity, we will initially only consider particles interacting in a one-dimensional space.

The Python code below shows how to determine the acceleration on each atom of argon due to each other atom of argon. It is possible to increase the efficiency of this algorithm by applying Newton’s third law, e.g. the force on atom $i$ will be equal and opposite to the force on atom $j$.

mass_of_argon = 39.948 # amu def get_accelerations(positions): """ Calculate the acceleration on each particle as a result of each other particle. N.B. We use the Python convention of numbering from 0. Parameters ---------- positions: ndarray of floats The positions, in a single dimension, for all of the particles (Å) Returns ------- ndarray of floats The acceleration on each particle (eV/Åamu) """ accel_x = np.zeros((positions.size, positions.size)) for i in range(0, positions.size - 1): for j in range(i + 1, positions.size): r_x = positions[j] - positions[i] rmag = np.sqrt(r_x * r_x) force_scalar = lj_force(rmag, 0.0103, 3.4) force_x = force_scalar * r_x / rmag accel_x[i, j] = force_x / mass_of_argon #eV Å-1 amu-1 # appling Newton's third law accel_x[j, i] = - force_x / mass_of_argon return np.sum(accel_x, axis=0) accel = get_accelerations(np.array([1, 5, 10])) print('Acceleration on particle 0 = eV/Åamu'.format( accel[0])) print('Acceleration on particle 1 = eV/Åamu'.format( accel[1])) print('Acceleration on particle 2 = eV/Åamu'.format( accel[2])) 

Acceleration on particle 0 = 1.453e-04 eV/Åamu Acceleration on particle 1 = -4.519e-05 eV/Åamu Acceleration on particle 2 = -1.002e-04 eV/Åamu 

Integration

Now that we have seen how to obtain the acceleration on our particles, we can apply the Newtonian equations of motion to probe the particles trajectory,

where, $\Delta t$ is the timestep (how far in time is incremented), $\mathbf_i$ is the particle position, $\mathbf_i$ is the velocity, and $\mathbf_i$ the acceleration. This pair of equations is known as the Velocity-Verlet algorithm, which can be written as:

1. Calculate the force (and therefore acceleration) on the particle
2. Find the position of the particle after some timestep
3. Calculate the new forces and accelerations
4. Determine a new velocity for the particle, based on the average acceleration at the current and new positions
5. Overwrite the old acceleration values with the new ones, $\mathbf_i(t) = \mathbf_i(t+\Delta t)$
6. Repeat

After the initial relaxation of the particles to equilibrium, this process can be continued for as long as is required to get sufficient statistics for the quantity you are intereseting in.

The Python code below is a set of two function for the above equations, these will be applied later.

def update_pos(x, v, a, dt): """ Update the particle positions. Parameters ---------- x: ndarray of floats The positions of the particles in a single dimension (Å) v: ndarray of floats The velocities of the particles in a single dimension (eVs/Åamu) a: ndarray of floats The accelerations of the particles in a single dimension (eV/Åamu) dt: float The timestep length (s) Returns ------- ndarray of floats: New positions of the particles in a single dimension (Å) """ return x + v * dt + 0.5 * a * dt * dt def update_velo(v, a, a1, dt): """ Update the particle velocities. Parameters ---------- v: ndarray of floats The velocities of the particles in a single dimension (eVs/Åamu) a: ndarray of floats The accelerations of the particles in a single dimension at the previous timestep (eV/Åamu) a1: ndarray of floats The accelerations of the particles in a single dimension at the current timestep (eV/Åamu) dt: float The timestep length (s) Returns ------- ndarray of floats: New velocities of the particles in a single dimension (eVs/Åamu) """ return v + 0.5 * (a + a1) * dt 

The above process is called the intergration step, and the Velocity-Verlet algorithm is the integrator. This function is highly non-linear for more than two particles. The result is that the integration step will only be valid for very small values of $\Delta t$, e.g. if a large timestep is used the acceleration calculated will not be accurate as the forces on the atom will change too significantly during it. The value for the timestep is usually on the order of 10 -15 s (femtoseconds). So in order to measure a nanosecond of “real-time” molecular dynamics, 1 000 000 (one million) iterations of the above algorithm must be performed. This can be very slow for large, realistic systems.

Initialisation

There are only two components left that we need to run a molecular dynamics simulation, and both are associated with the original configuration of the system; the original particle positions, and the original particle velocities.

The particle positions are usually either taken from some library of structures (e.g. the protein data bank if you are simulating proteins) or based on some knowledge of the system (e.g. CaF₂ is well known to have a face-centred cubic structure). For complex, multicomponent systems, software such as Packmol [1] may be used to build up the structure from its constituent parts. The importance of this initial structure cannot be overstated. For example if the initial structure is unrepresentative of the equilibrium structure, it may take a very long time before the equilibrium structure is obtained, possibly much longer than can be reasonably simulated.

The particle velocities are more general, as the total kinetic energy, $E_K$ of the system (and therefore the particle velocities) are dependent on the temperature of the simulation, $T$.

where, $m_i$ is the mass of particle $i$, $N$ is the number of particles, and $k_B$ is the Boltzmann constant. A common method to initialise the velocities is implemented in the Python function below.

from scipy.constants import Boltzmann def init_velocity(T, number_of_particles): """ Initialise the velocities for a series of particles. Parameters ---------- T: float Temperature of the system at initialisation (K) number_of_particles: int Number of particles in the system Returns ------- ndarray of floats Initial velocities for a series of particles (eVs/Åamu) """ R = np.random.rand(number_of_particles) - 0.5 return R * np.sqrt(Boltzmann * T / (mass_of_argon * 1.602e-19)) 

References

1. Martínez, L.; Andrade, R.; Birgin, E. G.; Martínez, J. M. J. Comput. Chem. 2009, 30 (13), 2157–2164. 10.1002/jcc.21224.

Источник