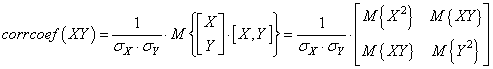Модуль числа питон numpy

Базовые математические функции

На этом занятии рассмотрим основные математические функции пакета NumPy, увидим, как они используются совместно с массивами.

Функции sum, mean, min и max

Итак, очень часто на практике требуется вычислять сумму значений элементов массива, их среднее значение, а также находить минимальные и максимальные значения. Для этих целей в NumPy существуют встроенные функции, выполняющие эти действия и сейчас мы посмотрим как они работают. Пусть, как всегда, у нас имеется одномерный массив:

a = np.array([ 1, 2, 3, 10, 20, 30])

Вычислим сумму, среднее значение и найдем максимальное и минимальное значения:

a.sum() # 66 a.mean() # 11.0 a.max() # 30 a.min() # 1

Как видите, все достаточно просто. Тот же самый результат будет получен и при использовании многомерных массивов. Например:

Но, если требуется вычислить сумму только по какой-то одной оси, то ее можно явно указать дополнительным параметром:

a.sum(axis=0) # array([24, 42]) a.sum(axis=1) # array([ 3, 13, 50])

Точно также работают и остальные три функции, например:

a.max(axis=0) # array([20, 30]) a.min(axis=1) # array([ 1, 3, 20])

Базовые математические функции

Предположим, имеется массив:

тогда для вычисления модулей значений его элементов можно записать команду:

np.abs(a) # array([ 1, 1, 5, 44, 32, 2])

На выходе получаем новый массив с абсолютными величинами. То же самое будет, если на вход подать обычный список значений:

np.abs([-1, 1, 5, -44, 32, ])# array([ 1, 1, 5, 44, 32])

Эти примеры демонстрируют разные типы входных данных: массив, список, число. Все это допустимо использовать в математических функциях.

Остальные функции работают по аналогии, например:

np.amax(a) # 32 np.log(a) # array([nan, 0. , 1.60943791, nan, 3.4657359,0.69314718]) np.around(0.7) # 1.0

Функции amin, amax, mean, argmax, argmin, при работе с многомерными матрицами, могут делать вычисления по строго определенной оси. Например:

a.resize(2, 3) np.amax(a, axis=0) # array([-1, 32, 5]) np.argmax(a, axis=1) # array([2, 1], dtype=int32)

Тригонометрические функции

Их использование также вполне очевидно. На входе они могут принимать массив, список или число. Если это угол, то он представляется в радианах. Например:

a = np.linspace(0, np.pi, 10) res1 = np.sin(a) # возвращает массив синусов углов np.sin(np.pi/3) np.cos([0, 1.57, 3.17]) res2 = np.cos(a) # возвращает массив косинусов углов np.arcsin(res1) # возвращает арксинусы от значений res1

Причем, все эти функции работают быстрее аналогичных функций языка Python. Поэтому, при использовании библиотеки NumPy предпочтение лучше отдавать именно ей, а не языку Python при тригонометрических вычислениях.

Функции генерации псевдослучайных чисел

Во многих программах требуется генерировать случайные значения и в NumPy для этого имеется специальный модуль random с богатым функционалом. Конечно, совершенно случайные величины получить невозможно, поэтому придумываются различные «хитрости» для их генерации и правильнее их называть – псевдослучанйыми числами.

В самом простом случае, функция rand() позволяет получать случайные числа в диапазоне от 0 до 1:

np.random.rand() # вещественное случайное число от 0 до 1

Если требуется получить массив из таких чисел, то можно указать это через первый аргумент:

np.random.rand(5) # array([0.78191696, 0.66581136, 0.46458873, 0.76416839, 0.28206656])

Для получения двумерных массивов – два аргумента:

np.random.rand(2, 3) # массив 2x3

И так далее. Можно создавать любые многомерные массивы из случайных величин.

Если требуется генерировать целые случайные значения, то используется функция randint():

np.random.randint(10) # генерация целых чисел в диапазоне [0; 10) np.random.randint(5, 10)# генерация в диапазоне [5; 10)

Для получения массива из таких случайных чисел дополнительно следует указать параметр size, следующим образом:

np.random.randint(5, size=4) # array([3, 1, 1, 4]) np.random.randint(1, 10, size=(2, 5)) # матрица 2x5

Функции rand() и randint() генерируют числа с равномерным законом распределения. Если нужно получать значения с другими широко известными распределениями, то используются функции:

np.random.randn() # нормальная СВ с нулевым средним и единичной дисперсией np.random.randn(5) # массив из пяти нормальных СВ np.random.randn(2, 3) # матрица 2x3 из нормальных СВ np.random.pareto(2.0, size=3) # распределение Паретто с параметром 2,0 np.random.beta(0.1, 0.3, size=(3, 3)) # бета-распределение с параметрами 0,1 и 0,3

Существуют и другие функции для генерации самых разных распределений. Документацию по ним можно посмотреть на официальном сайте пакета NumPy:

По умолчанию, все рассмотренные функции при каждом новом запуске генерируют разные числа. Однако, иногда требуются одни и те же их реализации. Например, такой подход часто используется для сохранения начальных случайных значений весов в нейронных сетях. Для этого устанавливают некое начальное значение зерна (seed):

np.random.seed(13) # начальное значение генератора случайных чисел

и все последующие запуски будут давать одну и ту же последовательность чисел, например:

np.random.randint(10, size=10) # array([2, 0, 0, 6, 2, 4, 9, 3, 4, 2])

Причем, у вас должны получиться такие же числа. Если запустим эту функцию еще раз, то будут получены следующие 10 случайных чисел:

np.random.randint(10, size=10) # array([6, 5, 9, 4, 2, 0, 3, 5, 3, 6])

Но, установив зерно снова в значение, например, 13:

np.random.randint(10, size=10) # array([2, 0, 0, 6, 2, 4, 9, 3, 4, 2]) np.random.randint(10, size=10) # array([6, 5, 9, 4, 2, 0, 3, 5, 3, 6])

Функции перемешивания элементов массива

np.random.shuffle() и np.random.permutation()

перемешивают случайным образом элементы массива. Например, дан массив:

a = np.arange(10) # array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

И нам требуется перетасовать его элементы. В самом простом случае, это делается так:

np.random.shuffle(a) # array([8, 7, 9, 6, 3, 4, 0, 2, 1, 5])

Причем, здесь меняется сам массив a. Если вызвать эту функцию еще раз:

np.random.shuffle(a) # array([7, 2, 1, 5, 8, 6, 4, 3, 9, 0])

то значения еще раз перетасуются. Но, работает она только с первой осью axis0. Например, если взять двумерный массив:

a = np.arange(1, 10).reshape(3, 3)

то в массиве aбудут переставлены только строки:

Вторая функция возвращает случайную последовательность чисел, генерируя последовательность «на лету»:

np.random.permutation(10) # array([8, 2, 7, 1, 0, 5, 3, 9, 4, 6])

Функции математической статистики

Рассмотрим работу этих функций. Предположим, имеются следующие векторы:

x = np.array([1, 4, 3, 7, 10, 8, 14, 21, 20, 23]) y = np.array([4, 1, 6, 9, 13, 11, 16, 19, 15, 22])

Эти числа будем воспринимать как реализации случайных величин X и Y. Тогда, для вычисления медианы СВX, можно воспользоваться функцией:

Для расчета дисперсии и СКО, функциями:

np.var(x) # дисперсия СВX на основе реализации x np.std(y) # СКО СВY на основе реализации y

Далее, чтобы рассчитать коэффициент корреляции Пирсона, объединим массивыx и y построчно:

XY = np.vstack([x, y]) # матрица 2x10

Результатом будет матрица 2×2:

array([[1. , 0.93158099],
[0.93158099, 1. ]])

Как ее следует интерпретировать? В действительности, это автоковариационная матрица вектора СВ[X, Y]:

(В этой формуле полагается, что СВX и Y центрированы, то есть имеют нулевое математическое ожидание).

Если нужно вычислить не нормированное МО, то есть, автоковариационную матрицу, то следует воспользоваться функцией:

np.cov(XY) # ковариационная матрица размерностью 2x2

Наконец, для вычисления взаимной корреляции между двумя векторамиx и y, используется функция:

np.correlate(x, y) # array([1736])

Более детальную информацию по этим статистическим функциям можно найти в официальной документации пакета NumPy:

Конечно, мы рассмотрели далеко не все математические функции NumPy. На следующем занятии продолжим эту тему и поговорим об умножении векторов и матриц, линейной алгебре и множествах.

Видео по теме

#1. Пакет numpy — установка и первое знакомство | NumPy уроки

#2. Основные типы данных. Создание массивов функцией array() | NumPy уроки

#3. Функции автозаполнения, создания матриц и числовых диапазонов | NumPy уроки

#4. Свойства и представления массивов, создание их копий | NumPy уроки

#5. Изменение формы массивов, добавление и удаление осей | NumPy уроки

#6. Объединение и разделение массивов | NumPy уроки

#7. Индексация, срезы, итерирование массивов | NumPy уроки

#8. Базовые математические операции над массивами | NumPy уроки

#9. Булевы операции и функции, значения inf и nan | NumPy уроки

#10. Базовые математические функции | NumPy уроки

#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy уроки

#12. Множества (unique) и операции над ними | NumPy уроки

#13. Транслирование массивов | NumPy уроки

© 2023 Частичное или полное копирование информации с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все тексты и изображения являются собственностью сайта

Источник

numpy.absolute#

A location into which the result is stored. If provided, it must have a shape that the inputs broadcast to. If not provided or None, a freshly-allocated array is returned. A tuple (possible only as a keyword argument) must have length equal to the number of outputs.

where array_like, optional

This condition is broadcast over the input. At locations where the condition is True, the out array will be set to the ufunc result. Elsewhere, the out array will retain its original value. Note that if an uninitialized out array is created via the default out=None , locations within it where the condition is False will remain uninitialized.

For other keyword-only arguments, see the ufunc docs .

Returns : absolute ndarray

An ndarray containing the absolute value of each element in x. For complex input, a + ib , the absolute value is \(\sqrt< a^2 + b^2 >\) . This is a scalar if x is a scalar.

>>> x = np.array([-1.2, 1.2]) >>> np.absolute(x) array([ 1.2, 1.2]) >>> np.absolute(1.2 + 1j) 1.5620499351813308 

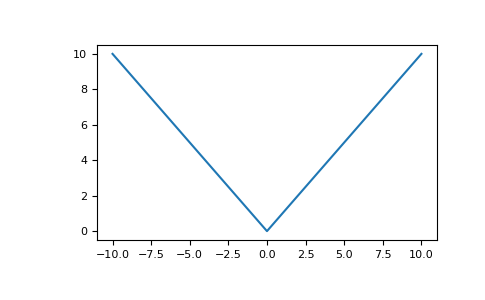
Plot the function over [-10, 10] :

>>> import matplotlib.pyplot as plt 

>>> x = np.linspace(start=-10, stop=10, num=101) >>> plt.plot(x, np.absolute(x)) >>> plt.show() 

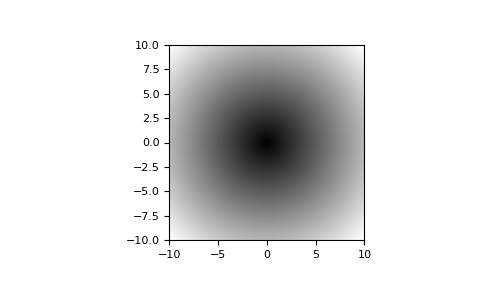
Plot the function over the complex plane:

>>> xx = x + 1j * x[:, np.newaxis] >>> plt.imshow(np.abs(xx), extent=[-10, 10, -10, 10], cmap='gray') >>> plt.show() 

The abs function can be used as a shorthand for np.absolute on ndarrays.

>>> x = np.array([-1.2, 1.2]) >>> abs(x) array([1.2, 1.2]) 

Источник

Функция abs() в Python

В этой статье мы представим функцию Python abs() с различными модулями, такими как NumPy и Pandas.

Python имеет огромное количество встроенных функций для выполнения математических и статистических операций. Одной из таких функций является функция abs().

Функция abs() function возвращает абсолютную величину или значение входных данных, переданных ей в качестве аргумента. Он возвращает фактическое значение ввода без учета знака.

Она принимает только один аргумент, который должен быть числом, и возвращает абсолютную величину числа.

• Если входные данные имеют тип integer или float — функция возвращает абсолютную величину / значение.
• Если введено complex number , функция abs() возвращает только часть величины числа.

num = -25.78 print("Absolute value:",abs(num))

Функция Pandas DataFrame.abs()

Модуль Python Pandas имеет встроенную DataFrame.abs() function для вычисления абсолютного значения всех значений данных, присутствующих в конкретной переменной / столбце данных фрейма данных набора данных.

import pandas as pd import numpy as np data = pd.read_csv("C:/marketing_tr.csv") data.head(10) data['cons.conf.idx'].abs()

В приведенном выше фрагменте кода мы использовали pandas.read_csv() function для импорта и загрузки набора данных в среду. Функция DataFrame.head(n) function фактически представляет первые n значений набора данных.

Далее мы выяснили абсолютные значения столбца cons.conf.idx.

0 42.0 1 42.7 2 36.4 3 42.7 4 46.2 . 7409 36.4 7410 42.7 7411 46.2 7412 42.0 7413 36.4 Name: cons.conf.idx, Length: 7414, dtype: float64

Функция numpy.absolute()

Модуль Python NumPy имеет numpy.absolute() function для получения абсолютных значений переданных ему элементов массива.

import numpy as np arr = [10, -20, 30, -40] abs_res = np.absolute(arr) print("The absolute values of the array elements:",abs_res)

The absolute values of the array elements: [10 20 30 40]

Источник