- Saved searches
- Use saved searches to filter your results more quickly
- License
- elbanic/SolarSystem
- Name already in use
- Sign In Required
- Launching GitHub Desktop
- Launching GitHub Desktop
- Launching Xcode
- Launching Visual Studio Code
- Latest commit
- Git stats
- Files
- README.md
- About
- Создаем симулятор солнечной системы
- Блог питониста
Saved searches
Use saved searches to filter your results more quickly
You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. Reload to refresh your session. You switched accounts on another tab or window. Reload to refresh your session.
A Simulation of Solar System
License
elbanic/SolarSystem
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
Name already in use
A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?
Sign In Required
Please sign in to use Codespaces.
Launching GitHub Desktop
If nothing happens, download GitHub Desktop and try again.
Launching GitHub Desktop
If nothing happens, download GitHub Desktop and try again.
Launching Xcode
If nothing happens, download Xcode and try again.
Launching Visual Studio Code
Your codespace will open once ready.
There was a problem preparing your codespace, please try again.
Latest commit
Git stats
Files
Failed to load latest commit information.
README.md
Simple Solar System by Python and PyGame
This software uses the following libraries & platform.
This software includes the following actions.
Installation of dependent libraries.
pip3 install pygame pip3 install pyopengl git clone https://github.com/elbanic/SolarSystem cd SolarSystem python3 main.py Following is the pygame license.
This library is distributed under GNU LGPL version 2.1, which can be found in the file «doc/LGPL». I reserve the right to place future versions of this library under a different license. http://www.gnu.org/copyleft/lesser.html This basically means you can use pygame in any project you want, but if you make any changes or additions to pygame itself, those must be released with a compatible license. (preferably submitted back to the pygame project). Closed source and commercial games are fine. The programs in the «examples» subdirectory are in the public domain.
About
A Simulation of Solar System
Создаем симулятор солнечной системы
Предисловие
Вечная тяга к новому подтолкнула к изучению такого замечательного языка программирования, как Питон. Как это часто бывает, отсутствие идеи, на реализацию которой не жалко потратить свое время, сильно тормозило процесс.
Волею судьбы на глаза попался замечательный цикл статей о создании игры-платформера на Питоне
тут и тут.
Я решил взяться за один старый проект. За симулятор движения тел под действием сил гравитации.
Что из этого вышло читайте дальше.
Часть первая. Теоритическая
Чтобы решить задачу, нужно сначала четко себе ее представить.
Предположим, всеми правдами и неправдами нам удалось заполучить двумерный участок безвоздушного пространства с находящимися в нем телами. Все тела перемещаются под действием сил гравитации. Внешнего воздействия нет.
Нужно построить процесс их движения относительно друг друга. Простота реализации и красочность конечного результата послужат стимулом и наградой. Освоение Питона будет хорошей инвестицией в будущее.
Пускай наша система состоит из двух тел:
1. массивной звезды массой М и центром (x0, y0)
2. легкой планеты массой m, с центром в точке (x, y), скоростью v = (vx, vy) и ускорением a = (ax, ay).
Когда нам удастся разобрать этот случай, мы легко перейдем к сложным системам со взаимным влиянием звезд и планет друг на друга. Сейчас же речь пойдет о самом простом.
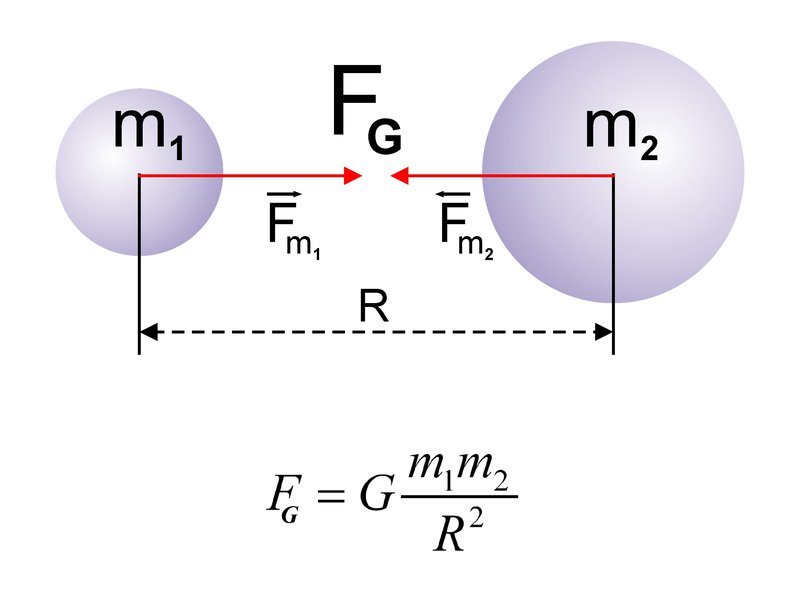
После несложных манипуляций со вторым законом Ньютона, законом всемирного тяготения и подобными треугольниками, я нашел, что:
ax = G * M * (x0-x) / r^3
ay = G * M * (y0-y) / r^3
Это позволяет составить алгоритм перемещения планеты в поле гравитации звезды:
1. Перед началом задаем начальное положение планеты (x, y) и начальную скорость (vx, vy)
2. На каждом шаге вычисляем новое ускорение по формуле выше, после этого пересчитываем скорость и координаты:
vx := vx + T * ax
vy := vy + T * ax
Осталось разобраться с константами G и T. Положим G = 1. Для нашей задачи это не так важно. Параметр T влияет на точность и скорость вычислений. Тоже положим 1 для начала.
Часть вторая. Практическая
Итак, моя первая программа на Питоне. При этом еще раз хочется поблагодарить Velese за практическое руководство.
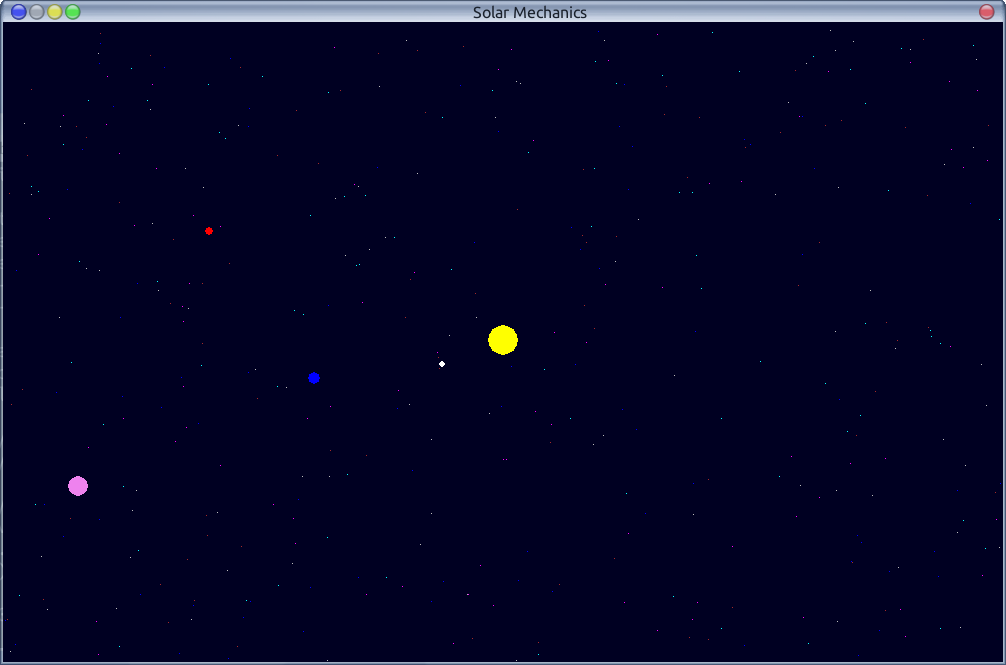
import pygame, math from pygame import * from math import * WIN_WIDTH = 800 WIN_HEIGHT = 640 PLANET_WIDTH = 20 PLANET_HEIGHT = 20 DISPLAY = (WIN_WIDTH, WIN_HEIGHT) SPACE_COLOR = "#000022" SUN_COLOR = "yellow" PLANET_COLOR = "blue" #Sun position X0 = WIN_WIDTH // 2 Y0 = WIN_HEIGHT // 2 #Sun mass M0 = 5000 #Stop conditions CRASH_DIST = 10 OUT_DIST = 1000 def main(): #PyGame init pygame.init() screen = pygame.display.set_mode(DISPLAY) pygame.display.set_caption("Solar Mechanics v0.1") #Space init bg = Surface((WIN_WIDTH,WIN_HEIGHT)) bg.fill(Color(SPACE_COLOR)) draw.circle (bg, Color(SUN_COLOR), (X0, Y0), 10) #Timer init timer = pygame.time.Clock() #Planet init planet = Surface((PLANET_WIDTH, PLANET_HEIGHT)) planet.fill(Color(SPACE_COLOR)) draw.circle (planet, Color(PLANET_COLOR), (PLANET_WIDTH // 2, PLANET_HEIGHT // 2), 5) #Planet to Sun distance r = 0.0 #Initial planet pos, speed and accel x = 100.0 y = 290.0 vx = 0.1 vy = 1.5 ax = 0.0 ay = 0.0 done = False while not done: timer.tick(50) for e in pygame.event.get(): if e.type == QUIT: done = True break r = sqrt((x - X0)**2 + (y - Y0)**2) ax = M0 * (X0 - x) / r**3 ay = M0 * (Y0 - y) / r**3 #New spped based on accel vx += ax vy += ay #New pos based on speed x += vx y += vy screen.blit(bg, (0, 0)) screen.blit(planet, (int(x), int(y))) pygame.display.update() if r < CRASH_DIST: done = True print("Crashed") break if r >OUT_DIST: done = True print("Out of system") break #Farewell print (":-)") if __name__ == "__main__": main() Так выглядит наша система после некоторого времени симуляции
Пока писалась эта заметка, симулятор разросся новой функциональностью: количество объектов в звездной системе не ограничевается, учитывается взаимное их влияние друг на друга, расчетная часть вынесена в свой класс, конфигурация системы задается в отдельном файле и добавлена возможность выбора систем.
Сейчас я занимаюсь поиском интересных сценариев системы и небольшими улучшениями интерфейса.
Вот пример того, что на данный момент в разработке:
Если эта заметка встретит положительные отзывы, обещаю продолжить рассказ о более новой версии.
1. Я благодарен всем комментаторам за критические замечания. Они дают большую пищу для размышлений.
2. Проект вырос. Все тела уже независимы, влияют друг на труга в соответствии с законом всемирного тяготения.Подсчитывается N^2 взаиможействий.
Сейчас есть возможность хранить конфигурации звездной системы во внешних файлах и выбирать на старте
Код тут
Запускать так: python3.3 main.py -f .ini
Различные конфигурации — там же.
3. Благодаря комментариям удалось найти и устранить главную недоработку — метод вычисления координат.
Сейчас используется метод Рунге-Кутты. По мере прочтения «Нежестких задач» буду осваивть новые методы.
Блог питониста
Есть такая библиотека — vpython, с помощью нее можно создавать различные анимации и рисовать 3d объекты. Интересно было бы смоделировать хотя бы очень простую версию Солнечной системы. У меня не получилось сделать это самому, поэтому я нанял человека на upwork, чтобы он помог мне. Код в данном посте не мой, а этого человека, я лишь немного изменил его.
Сначала установим vpython:
Попробуем нарисовать сферу:
1 from vpython import sphere 2 3 sphere()
Теперь, если все работает, начнем с того, что зададимся константами, нужными для дальнейших вычислений:
1 from vpython import sphere, vector, color, rotate 2 import math 3 4 # Константы 5 G = 6.667e-11 # гравитационная постоянная, м^3 кг^-1 с^-2 6 MS = 1.9885e30 # масса Солнца, кг 7 ME = 5.97e24 # масса Земли, кг 8 MM = 7.348e22 # масса Луны, кг 9 RSE = 1.496e11 # среднее расстояние от Солнца до Земли, метры 10 REM = 384.4e6 # расстояние от Земли до Луны
Далее вычислим гравитационные силы между Солнцем и Землей и между Землей и Луной по формуле:
1 # Гравитационная сила между Солнцем и Землей, Н 2 F_SE = G*MS*ME/(RSE*RSE) 3 # Гравитационная сила между Землей и Луной, Н 4 F_EM = G*ME*MM/(REM*REM)
Далее вычисляем угловые скорости и обычные по формулам
1 # Угловая скорость Луны 2 wm = math.sqrt(F_EM/(MM*REM)) 3 # Угловая скорость Земли 4 we = math.sqrt(F_SE/(ME*RSE))
Далее рисуем сами сферы, которые будут представлять Солнце, Землю и Луну, конечно размеры не в масштабе для наглядности:
1 v = vector(0.5, 0, 0) 2 E = sphere(pos=vector(3, 0, 0), color=color.blue, radius=.25, make_trail=True) 3 M = sphere(pos=E.pos+v, color=color.white, radius=0.08, make_trail=True) 4 S = sphere(pos=vector(0, 0, 0), color=color.yellow, radius=1)
Потом, используя полярные координаты, обновляем позиции тел при каждом шаге:
1 # Будем использовать полярные координаты 2 # Шаг 3 dt = 10 4 # углы поворота за один шаг: 5 theta_earth = we*dt 6 theta_moon = wm*dt 7 while dt 86400*365: 8 # Земля и Луна поворачиваются вокруг оси z (0,0,1) 9 Earth.pos = rotate(Earth.pos, angle=theta_earth, axis=vector(0, 0, 1)) 10 v = rotate(v, angle=theta_moon, axis=vector(0, 0, 1)) 11 Moon.pos = Earth.pos + v 12 dt += 10
1 from vpython import sphere, vector, color, rotate 2 import math 3 4 # Константы 5 G = 6.667e-11 # гравитационная постоянная, м^3 кг^-1 с^-2 6 MS = 1.9885e30 # масса Солнца, кг 7 ME = 5.97e24 # масса Земли, кг 8 MM = 7.348e22 # масса Луны, кг 9 RSE = 1.496e11 # среднее расстояние от Солнца до Земли, метры 10 REM = 384.4e6 # расстояние от Земли до Луны 11 # Гравитационная сила между Солнцем и Землей. Н 12 F_SE = G*MS*ME/(RSE*RSE) 13 # Гравитационная сила между Землей и Луной, Н 14 F_EM = G*ME*MM/(REM*REM) 15 # Угловая скорость Луны 16 wm = math.sqrt(F_EM/(MM*REM)) 17 # Угловая скорость Земли 18 we = math.sqrt(F_SE/(ME*RSE)) 19 20 v = vector(0.5, 0, 0) 21 Earth = sphere( 22 pos=vector(3, 0, 0), color=color.blue, radius=.25, make_trail=True) 23 Moon = sphere(pos=Earth.pos+v, color=color.white, radius=0.08, make_trail=True) 24 Sun = sphere(pos=vector(0, 0, 0), color=color.yellow, radius=1) 25 26 # Будем использовать полярные координаты 27 # Шаг 28 dt = 10 29 # углы поворота за один шаг: 30 theta_earth = we*dt 31 theta_moon = wm*dt 32 while dt 86400*365: 33 # Земля и Луна поворачиваются вокруг оси z (0,0,1) 34 Earth.pos = rotate(Earth.pos, angle=theta_earth, axis=vector(0, 0, 1)) 35 v = rotate(v, angle=theta_moon, axis=vector(0, 0, 1)) 36 Moon.pos = Earth.pos + v 37 dt += 10
Также, я сделал видео работы данного скрипта, по-моему, получилось неплохо: