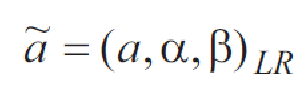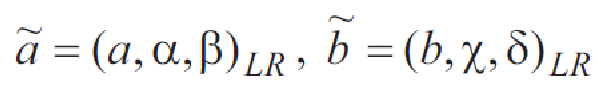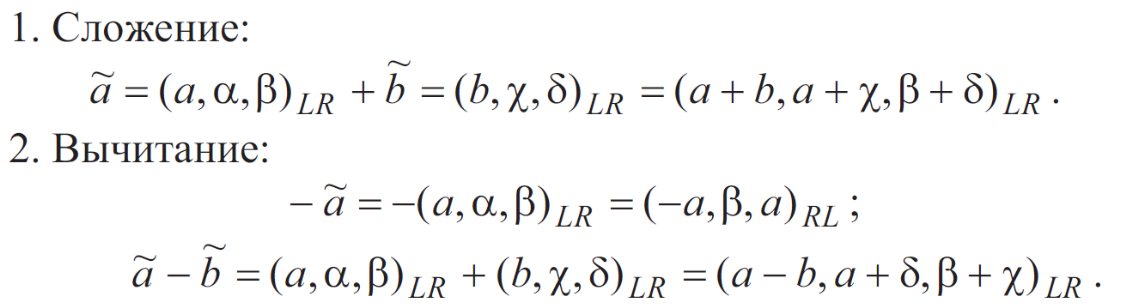24. Нечеткие числа: виды нечетких чисел; операции над нечеткими числами.
Нечеткой величиной называется произвольное нечеткое множеcтво заданное на множестве действительных чисел R 1 :
Нечетким числом называется нечеткая величина, функция принадлежности которой является выпуклой и унимодальной.
Нечеткие числа широко используются в повседневной жизни. Когда мы говорим: «приблизительно три», «приблизительно двадцать пять» и т. п., то тем самым предполагаем использование нечеткого числа. Формально нечеткое число можно рассматривать как нечеткое множество, заданное на множестве действительных чисел и обладающее некоторыми дополнительными свойствами.
Нечеткие числа во многих случаях применяются для непосредственных расчетов (см. например, расчеты чистого дисконтированного дохода, внутренней нормы рентабельности проекта разработки нефтегазового месторождения и др.). При этом, наиболее популярными и легко интерпретируемыми руководителями являются нечеткие числаLR -типа.
Нечеткие числа (L-R)-типа — это разновидность нечетких чисел специального вида, т.е. задаваемых по определенным правилам с целью снижения объема вычислений при операциях над ними.
Нечеткое число ã, называется нечетким числом LR-типа или LR-числом, если
где a — мода нечеткого числа LR-типа,α — левый коэффициент нечеткости,β — правый коэффициент нечеткости,L(x) — левая функция принадлежности,R(x) — правая функция принадлежности.
Символически число LR-типа, записываются следующим образом:
Арифметические операции над нечеткими числами LR-типа выполняются по следующим правилам. Пусть имеется два нечетких числа LR-типа:
25. Модели нечеткого математического программирования: оптимизация с нечеткими отношениями.
Оптимизация с нечеткими отношениями
В общем виде задача нечеткого математического программирования формулируется следующим образом — найти такой вектор x=(xi, x2, . , xn) , для которого
Решение этой задачи ищется на основе следующего подхода.
Пусть Ф0— значение критерияf(x), достижение которого считается достаточным для выполнения цели, тогда можно ввести некоторыеd иli — пороговые уровни, такие, что выполняются неравенства:
которые означают сильное нарушение неравенств
определяющих возможные варианты решения задачи.
При таком подходе возможно для критериев оптимальности и ограничений ввести функции принадлежности решения к допустимому и оптимальному решению. В результате исходная задача оказывается сформулированной в форме задачи достижения нечетко определенной цели при нечетких ограничениях и для ее решения может быть применен подход Белмана-Заде.
К такого рада задачам в силу особенностей нефтегазодобывающего производства можно отнести: планирование геофизических исследований скважин (ГИС), техническое обслуживание и ремонт различных технологических объектов. В общем виде они могут быть записаны в виде следующей оптимизационной задачи
Где xij равно 1 — если j -й вид работ (вариант разработки месторождения комплекс ГИС, ТОР и др.) назначается на 1-й вид объектов,
aij h количество ресурсов h-го типа, необходимое для проведения j-го вида работ на i-ом виде объектов;
A h — количество ресурса h-го типа, (время работы МТР, ремонтных бригад, стоимость работ и т.п.), имеющееся в системе;
сij — обобщенная (комплексная) эффективность применения j-го вида работ на i-ом виде объектов.
Известно, что четкий вариант задачи (6.1)-(6.5) хорошо решается методом ветвей и границ или с помощью L-алгоритма. При этом лишь некоторое исключение представляет собой задача распределения ГИС и ТОР по плановым периодам, имеющая в своем составе отличный от (6.1) вид критерия оптимальности, особенность которого состоит в том, что заранее, до начала решения задачи невозможно иметь значения Cij (они вычисляются в ходе решения задачи).
Однако, для всех перечисленных в начале этого раздела задач общими характерными моментами является то, что: 1) правые части ресурсных ограничений представляют собой некоторые средние значения полученные, например, в результате применения моделей теории массового обслуживания; 2) значения коэффициентов Cij, тоже, как правило, носят качественный (приближенный) характер и получаются в результате качественного экспертного анализа). Поэтому здесь имеется три альтернативных подхода для выбора методов (алгоритмов) решения этих задач.
Первый подход основан на том, что значения коэффициентов aij h ,A h , сij считаются хорошо определенными и для решения задачи применяются упомянутые выше метод «ветвей и границ» илиL-алгоритм .
Второй подход основан на том, что aij h ,A h , сij имеют статистическую неопределенность. Тогда задача (6.1)-(6.5) становится М-задачей стохастического математического программирования, методы и трудности решения которой также хорошо известны. Наконец, третий подход может быть основан на том, что неопределенность коэффициентов сij в большей степени связана с не достаточностью информации и не носит ярко выраженной статистической неопределенности. В свою очередь можно допустить, так же, что при решении задачи (6.1)-(6.5) ресурсные ограничения могут выполняться лишь с определенной степенью точности, например в пределах среднеквадратического отклонения (или в пределах заданных экспертным путем, что в практической ситуации бывает достаточно часто). Учитывая это, задача (6. 1)-(6.5) может быть интерпретирована как обобщенная распределительная задача с нечетко поставленной целью и ограничениями.
Алгоритмы нечеткой оптимизации
Главная цель нечеткого математического программирования — помочь лицу, принимающему решение, разобраться в выдвинутых им допущениях. Нечеткий подход не подменяет собой простейшего анализа в поисках разумной точности. Он облегчает задачу лица, принимающего решения, позволяя не формулировать явно точные ограничения. Вот почему плодотворный обмен идеями между теорией нечетких множеств и классическим программированием может явиться значительным шагом к созданию новых методов.
Стандартная задача нечеткого математического программирования формулируется обычно как задача максимизации (или минимизации) заданной функции на заданном множестве допустимых альтернатив, которое описывается системой равенств или неравенств. Например:
Нечеткий вариант этой задачи получается, если «смягчить» ограничения, т.е. допустить возможность их нарушения с той или иной степенью. Кроме того, вместо максимизации функции можно стремиться к достижению некоторого заданного значения этой функции, причем различным отклонениям значения функции от этой величины приписывать разные степени допустимости.
Задача 3. Нечетко описана «максимизируемая» функция , т.е. задано отображение ![\(\mu _\varphi ;X \times R \to [0,1]\)](https://intuit.ru/sites/default/files/tex_cache/c53b18bf6e50aedc3a73ca3d5743ba05.png)


В этом случае функция Решение можно определить как нечеткое подмножество универсального множества альтернатив. Оптимум соответствует той области Очевидно, что в реальных ситуациях неразумно проводить резкую границу для множества допустимых альтернатив. Может случится так, что распределения, попадающие за эту границу, дадут эффект, более желательный для лица, принимающего решения. Например, ясно, что при несовместных распределениях эта область пустая. В таком случае налицо необходимость модификации ограничений. Желательно выяснить, как изменить ограничения задачи, чтобы появились допустимые решения и задача стала разрешимой. В таких случаях представляется целесообразным вводить нечеткое множество допустимых элементов и, следовательно, рассматривать проблему как задачу нечеткого математического программирования с применением подхода, дающего человеку больше свободы в использовании его субъективных представлений о ситуации. Формы нечеткого описания исходной информации в задачах принятия решений могут быть различными; отсюда и различия в математических формулировках соответствующих задач нечеткого математического программирования .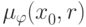
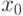
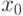

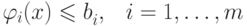



( 2)