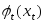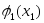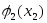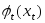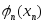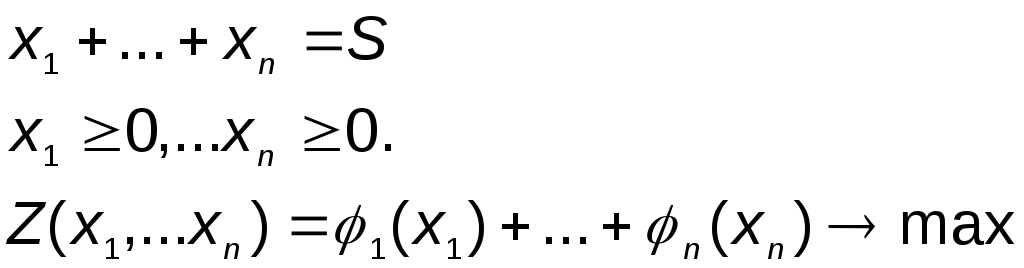Тема 9. Модели и методы динамического программирования
9.1. Моделирование процессов наилучшего распределения ресурсов методом динамического программирования
Основные идеи, приведшие к созданию метода динамического программирования, развиты американским ученым Беллманом в начале 1950-х годов.
В задачах динамического программирования процесс принятия решений распадается на ряд последовательных этапов, что дает возможность принять ряд последовательных решений, обеспечивающих оптимальность развития экономического процесса в целом. В результате строится такая вычислительная схема, согласно которой решение сложной многовариантной задачи заменяется многократным решением относительно простой задачи, что позволяет значительно сократить объем вычислений.
Представим себе некоторый процесс, распадающийся на несколько этапов, например производство на предприятии в течение ряда лет. Пусть эффективность деятельности предприятия характеризуется некоторым показателем, например получаемой прибылью. Для функционирования предприятия в каждый из годов t = 1, . n используется некоторый ресурс (например, капиталовложения), причем потребление этого ресурса за n лет не должно превысить заданную величину S.
Известно, что при выделении ресурса в количестве хt в год предприятие получает прибыль в размере .
Покажем возможные распределения ресурса и получаемой прибыли по годам:
Покажем динамику получения прибыли:
Итак, от распределения ресурса во времени существенно зависит и динамика получаемой прибыли.
Требуется так распределить ресурс S по годам рассматриваемого периода, чтобы суммарная прибыль была максимальной, т.е. необходимо найти такой неотрицательный вектор Х = (х1, . хn), при котором функция прибыли Z принимает наибольшее значение.
Математическую модель такого распределения можно записать следующим образом:
Отсюда видно, что сумма прибыли складывается из прибылей, получаемых по годам. Процесс распределения ресурса, о котором идет речь, это управляемый процесс, т.е. мы может выбирать параметры хt, которые влияют как на получение прибыли в каждом году, так и на общую величину прибыли.
Процесс распределения, например капиталовложений, в динамике естественным образом распадается на n шагов, где t-й шаг — это выделение предприятию капиталовложений в году t.
Такую же математическую модель получим, если ресурс будет распределяться не по годам, а между n различных предприятий в одном периоде (году).
Аналогичную модель получим, если рассмотрим задачу о распределении заданного объема работ по разным видам оборудования.
В соответствии с объемом выполняемой работы могут существенно различаться и эксплуатационные расходы. Задача может состоять в таком распределении работ по видам оборудования, чтобы суммарные эксплуатационные расходы были минимальными.
Любую многошаговую задачу можно решать по-разному: или все параметры находить сразу, за один шаг, или строить оптимальное управление постепенно, шаг за шагом.
Обычно второй способ значительно проще, особенно при большом числе шагов.
Идея последовательной оптимизации и составляет суть метода динамического программирования.
Нельзя считать пошаговой или последовательной оптимизацией то, что вся задача разбивается на ряд малых, которые решаются отдельно и независимо друг от друга.
Решение, принимаемое на одном шаге, должно быть дальновидным, учитывающим все последствия, к которым оно может привести в будущем.
Только на последнем шаге решение может быть принято без прогноза на будущее. На последнем шаге метода динамического программирования оптимизация означает максимальную эффективность только одного этого шага.
Проиллюстрируем идею метода динамического моделирования на примере задачи оптимального распределения ресурсов.
Рассмотрим следующую ситуацию.
Объединение располагает финансовыми средствами в 5 млн. руб., которые оно намерено использовать для реконструкции и модернизации четырех своих предприятий. В зависимости от величины используемых капиталовложений предприятие ежегодно получает прирост прибыли в размерах, показанных таблице:
Тема 8. Модели динамического программирования
Динамическое программирование связано с возможностью представления процесса управления в виде цепочки последовательных действий или шагов, развернутых во времени и ведущих к цели. Таким образом, процесс управления можно разделять на части и представить его в виде динамической последовательности и интерпретировать в виде пошаговой программы, развернутой во времени. Это позволяет спланировать программу будущих действий. Поскольку вариантов возможных планов — программ множество, то, необходимо из них выбрать лучший, оптимальный по какому-либо критерию в соответствии с поставленной целью.
1. Предмет динамического программирования
Динамическое программирование представляет собой математический аппарат, который подходит к решению некоторого класса задач путем их разложения на части, небольшие и менее сложные задачи. При этом отличительной особенностью является решение задач по этапам, через фиксированные интервалы, промежутки времени, что и определило появление термина динамическое программирование. Следует заметить, что методы динамического программирования успешно применяются и при решении задач, в которых фактор времени не учитывается. В целом математический аппарат можно представить как пошаговое или поэтапное программирование. Решение задач методами динамического программирования проводится на основе сформулированного Р. Э. Беллманом принципа оптимальности: оптимальное поведение обладает тем свойством, что каким бы ни было первоначальное состояние системы и первоначальное решение, последующее решение должно определять оптимальное поведение относительно состояния, полученного в результате первоначального решения.
Из этого следует, что планирование каждого шага должно проводиться с учетом общей выгоды, получаемой по завершении всего процесса, что и позволяет оптимизировать конечный результат по выбранному критерию.
Таким образом, динамическое программирование в широком смысле представляет собой оптимальное управление процессом, посредством изменения управляемых параметров на каждом, и, следовательно, воздействуя на ход процесса, изменяя на каждом шаге состояние системы.
В целом динамическое программирование представляет собой стройную теорию для восприятия и достаточно простую для‚ применения в коммерческой деятельности при решении как линейных, так и нелинейных задач.
Динамическое программирование (ДП) является одним из разделов оптимального программирования. Для него характерны специфические методы и приемы, применительные к операциям, в которых процесс принятия решения разбит на этапы (шаги). Методами ДП решаются вариантные оптимизационные задачи с заданными критериями оптимальности, с определенными связями между переменными и целевой функцией, выраженными системой уравнений или неравенств. При этом, как и в задачах, решаемых методами линейного программирования, ограничения могут быть даны в виде равенств или неравенств. Однако если в задачах линейного программирования зависимости между критериальной функцией и переменными обязательно линейны, то в задачах ДП эти зависимости могут иметь еще и нелинейный характер. ДП можно использовать как для решения связанных с динамикой процесса или системы, так и для статических задач, связанных, например, с распределением ресурсов. Это значительно расширяет область применения ДП для решения задач управления. А возможность упрощения процесса, которая достигается за счет ограничения области и количества исследуемых при переходе к очередному этапу вариантов увеличивает достоинства этого комплекса методов.
Вместе с тем ДП свойственны и недостатки. Прежде всего в нем нет единого универсального метода решения. Практически каждая задача, решаемая этим методом, характеризуется своими особенностями и требует проведения поиска наиболее приемлемой совокупности методов для ее решения. Кроме того, большие объемы и трудоемкость решения многошаговых задач, имеющих множество состояний, приводят к необходимости отбора задач малой размерности либо использования сжатой информации. Последнее достигается с помощью методов анализа вариантов и переработки списка состояний. Для процессов с непрерывным временем ДП рассматривается как предельный вариант дискретной схемы решения. Получаемые при этом результаты практически совпадают с теми, которые получаются методами максимума Л. С. Понтрягина или Гамильтона — Якоби — Беллмана. ДП применяется для решения задач, в которых поиск оптимума возможен при поэтапном подходе, например, распределение дефицитных капитальных вложений между новыми направлениями их использования; разработка правил управления спросом или запасами, устанавливающими момент пополнения запаса и размер пополняющего заказа; разработка принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию; составления календарных планов текущего и капитального ремонтов оборудования и его замены; поиск кратчайших расстояний на транспортной сети, формирование последовательности развития коммерческой операции и т.д.