Параллельное программирование в Python при помощи multiprocessing и shared array
Python замечательный язык. Связка Python + NumPy + Matplotlib, на мой взгляд, сейчас одна из лучших для научных расчётов и быстрого прототипирования алгоритмов. Но у каждого инструмента есть свои светлые и тёмные стороны. Одной из самых дискутируемых особенностей Python является GIL – Global Interpreter Lock. Я бы отнёс эту особенность к тёмной стороне инструмента. Хотя многие со мной не согласятся.
Если кратко, то GIL не позволяет в одном интерпретаторе Python эффективно использовать больше одного потока. Защитники GIL утверждают, что однопоточные программы при наличии GIL работают намного эффективнее. Но наличие GIL означает, что параллельные вычисления с использованием множества потоков и общей памяти невозможны. А это достаточно сильное ограничения в современном многоядерном мире.
Один из способов преодоления GIL при помощи потоков на C++ был недавно рассмотрен в статье: Использование Python в многопоточном приложении на C++. Я же хочу рассмотреть другой способ преодоления ограничений GIL, основанный на multiprocessing и shared array. На мой взгляд, этот способ позволяет достаточно просто и эффективно использовать процессы и разделяемую память для прозрачного параллельного программирования в стиле множества потоков и общей памяти.
Задача.
В качестве примера рассмотрим следующую задачу. В трёхмерном пространстве заданы N точек v0, v1, …, vN. Требуется для каждой пары точек вычислить функцию, зависящую от расстояния между ними. Результат будет представлять собой матрицу NxN со значениями этой функции. В качестве функции возьмем следующую: f = r^3 / 12 + r^2 / 6. Этот тест, на самом деле, не такой уж и синтетический. На вычислении таких функций от расстояния основана RBF интерполяция, которая используется во многих областях вычислительной математики.
Способ параллелизации.
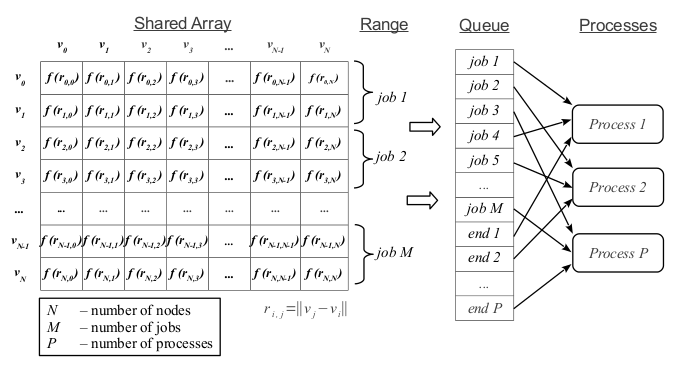
В данной задаче каждая строка матрицы может вычисляться независимо. Из каждых нескольких строк матрицы сформируем независимые работы и поместим их в очередь заданий (см. рис. 1). Запустим несколько процессов. Каждый процесс будет брать из очереди следующее задание на выполнение, пока не встретит специальное задание с кодом «end». В этом случае процесс заканчивает свою работу.
Реализация на Python.
В реализации на Python у нас будут два главных метода: mpCalcDistance(nodes) и
mpCalcDistance_Worker(nodes, queue, arrD). Метод mpCalcDistance(nodes) принимает на вход список узлов, создает область общей памяти, подготавливает очередь заданий и запускает процессы. Метод mpCalcDistance_Worker(nodes, queue, arrD) это вычислительный метод, работающий в собственном потоке. Он принимает на вход список узлов, очередь заданий и область общей памяти. Рассмотрим реализацию этих методов подробнее.
Метод mpCalcDistance(nodes)
nP = nodes.shape[0] nQ = nodes.shape[0] arrD = mp.RawArray(ctypes.c_double, nP * nQ) Создаем очередь заданий. Каждое задание не что иное, как просто диапазон строчек матрицы. Специальное значение None это признак завершения работы процесса:
nCPU = 2 nJobs = nCPU * 36 q = nP / nJobs r = nP % nJobs jobs = [] firstRow = 0 for i in range(nJobs): rowsInJob = q if (r > 0): rowsInJob += 1 r -= 1 jobs.append((firstRow, rowsInJob)) firstRow += rowsInJob queue = mp.JoinableQueue() for job in jobs: queue.put(job) for i in range(nCPU): queue.put(None) workers = [] for i in range(nCPU): worker = mp.Process(target = mpCalcDistance_Worker, args = (nodes, queue, arrD)) workers.append(worker) worker.start() queue.join() D = np.reshape(np.frombuffer(arrD), (nP, nQ)) return D Метод mpCalcDistance_Worker(nodes, queue, arrD)
nP = nodes.shape[0] nQ = nodes.shape[0] D = np.reshape(np.frombuffer(arrD), (nP, nQ)) while True: job = queue.get() if job == None: break start = job[0] stop = job[0] + job[1] # components of the distance vector p = nodes[start:stop] q = nodes.T Rx = p[:, 0:1] - q[0:1] Ry = p[:, 1:2] - q[1:2] Rz = p[:, 2:3] - q[2:3] # calculate function of the distance L = np.sqrt(Rx * Rx + Ry * Ry + Rz * Rz) D[start:stop, :] = L * L * L / 12 + L * L / 6 queue.task_done() Результаты
Среда выполнения: двухядерный процессор, Ubuntu 12.04, 64bit. 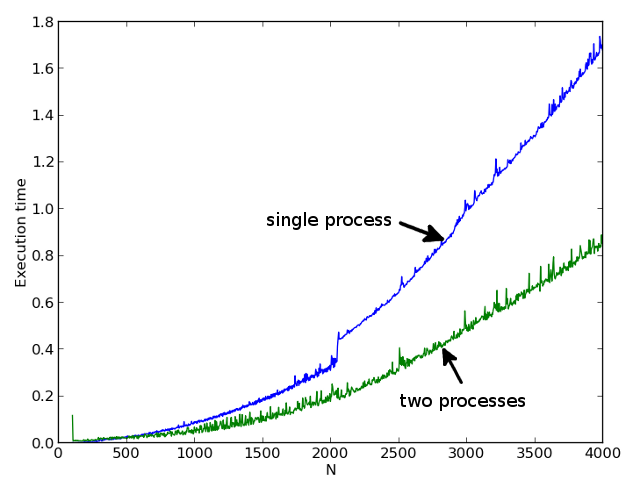
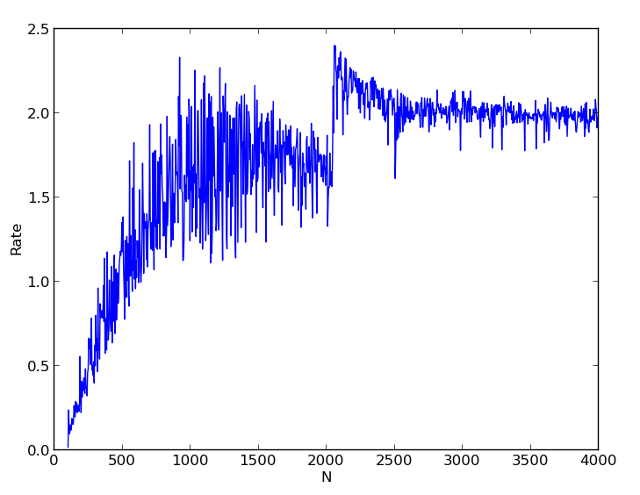
На первой картинке показаны времена однопоточного и двухпоточного расчета для различных N. На второй картинке показано отношение времени однопоточного расчета к двухпоточному. Видно, что начиная с N = 500 мы получаем уже существенное ускорение расчета.
Очень интересный результат получается в районе числа N = 2000. В однопоточном варианте мы получаем заметный скачок времени расчета, а при многопоточном расчете коэффициент ускорения даже превышает 2. Я объясняю это эффектом кэша. В многопоточном варианте данные для каждой задачи полностью умещаются в кэш. А в однопоточном уже нет.
Так что использование процессов и общей памяти, на мой взгляд, достаточно просто позволяет обойти ограничения GIL.
""" Python multiprocessing with shared memory example. This example demonstrate workaround for the GIL problem. Workaround uses processes instead of threads and RawArray allocated from shared memory. See also: [1] http://docs.python.org/2/library/multiprocessing.html [2] http://folk.uio.no/sturlamo/python/multiprocessing-tutorial.pdf [3] http://www.bryceboe.com/2011/01/28/the-python-multiprocessing-queue-and-large-objects/ """ import time import ctypes import multiprocessing as mp import numpy as np import matplotlib.pyplot as plt def generateNodes(N): """ Generate random 3D nodes """ return np.random.rand(N, 3) def spCalcDistance(nodes): """ Single process calculation of the distance function. """ p = nodes q = nodes.T # components of the distance vector Rx = p[:, 0:1] - q[0:1] Ry = p[:, 1:2] - q[1:2] Rz = p[:, 2:3] - q[2:3] # calculate function of the distance L = np.sqrt(Rx * Rx + Ry * Ry + Rz * Rz) D = L * L * L / 12 + L * L / 6 return D def mpCalcDistance_Worker(nodes, queue, arrD): """ Worker process for the multiprocessing calculations """ nP = nodes.shape[0] nQ = nodes.shape[0] D = np.reshape(np.frombuffer(arrD), (nP, nQ)) while True: job = queue.get() if job == None: break start = job[0] stop = job[0] + job[1] # components of the distance vector p = nodes[start:stop] q = nodes.T Rx = p[:, 0:1] - q[0:1] Ry = p[:, 1:2] - q[1:2] Rz = p[:, 2:3] - q[2:3] # calculate function of the distance L = np.sqrt(Rx * Rx + Ry * Ry + Rz * Rz) D[start:stop, :] = L * L * L / 12 + L * L / 6 queue.task_done() queue.task_done() def mpCalcDistance(nodes): """ Multiple processes calculation of the distance function. """ # allocate shared array nP = nodes.shape[0] nQ = nodes.shape[0] arrD = mp.RawArray(ctypes.c_double, nP * nQ) # setup jobs #nCPU = mp.cpu_count() nCPU = 2 nJobs = nCPU * 36 q = nP / nJobs r = nP % nJobs jobs = [] firstRow = 0 for i in range(nJobs): rowsInJob = q if (r > 0): rowsInJob += 1 r -= 1 jobs.append((firstRow, rowsInJob)) firstRow += rowsInJob queue = mp.JoinableQueue() for job in jobs: queue.put(job) for i in range(nCPU): queue.put(None) # run workers workers = [] for i in range(nCPU): worker = mp.Process(target = mpCalcDistance_Worker, args = (nodes, queue, arrD)) workers.append(worker) worker.start() queue.join() # make array from shared memory D = np.reshape(np.frombuffer(arrD), (nP, nQ)) return D def compareTimes(): """ Compare execution time single processing versus multiple processing. """ nodes = generateNodes(3000) t0 = time.time() spD = spCalcDistance(nodes) t1 = time.time() print "single process time: s.".format(t1 - t0) t0 = time.time() mpD = mpCalcDistance(nodes) t1 = time.time() print "multiple processes time: s.".format(t1 - t0) err = np.linalg.norm(mpD - spD) print "calculate error: ".format(err) def showTimePlot(): """ Generate execution time plot single processing versus multiple processing. """ N = range(100, 4000, 4) spTimes = [] mpTimes = [] rates = [] for i in N: print i nodes = generateNodes(i) t0 = time.time() spD = spCalcDistance(nodes) t1 = time.time() sp_tt = t1 - t0 spTimes.append(sp_tt) t0 = time.time() mpD = mpCalcDistance(nodes) t1 = time.time() mp_tt = t1 - t0 mpTimes.append(mp_tt) rates.append(sp_tt / mp_tt) plt.figure() plt.plot(N, spTimes) plt.plot(N, mpTimes) plt.xlabel("N") plt.ylabel("Execution time") plt.figure() plt.plot(N, rates) plt.xlabel("N") plt.ylabel("Rate") plt.show() def main(): compareTimes() #showTimePlot() if __name__ == '__main__': main()