Методы одномерной минимизации python

Хитрость в том, чтобыиспользовать вектор в качестве входных данных для целевой функциии убедиться, что целевая функция по-прежнему возвращает единственное скалярное значение Кроме того, поскольку проблема оптимизации заключается в максимизации целевой функции, нам нужноизменить знак и вернуть отрицательныйсуммы гауссовых функций как результат целевой функции.

Поэтому вполне возможно использовать подпрограммы оптимизации SciPy для решения проблемы ML.

Это дает вам глубокое понимание фактической работы алгоритма, так как вы должны сами строить метрику потерь, а не зависеть от какой-то готовой, готовой к использованию функции.

Оптимизация гиперпараметра в ОД

Настройка параметров и гиперпараметров моделей ML часто является громоздкой и подверженной ошибкам задачей. Хотя для поиска наилучшей параметрической комбинации доступны методы поиска по сетке, некоторая степень автоматизации может быть легко введеназапуск цикла оптимизации над пространством параметров, В этом случае целевой функцией должна быть некоторая метрика качества предсказания модели ML (например, среднеквадратическая ошибка, показатель сложности или показатель F1).

Использование машинного обучения в качестве оценщика функций

Во многих ситуациях у вас не может быть хорошей аналитической функции в закрытой форме для использования в качестве цели задачи оптимизации.

Но кому важно быть хорошим, когда у нас есть глубокое обучение?

Вообразите силумодель оптимизации, которая снабжается (для ее целевой функции, а также для ограничений) множеством моделей— различаются по своей сути, но стандартизированы по отношению к формату вывода, чтобы они могли действовать в унисон.

Вы можете выбрать аналитическую функцию, сеть глубокого обучения (возможно, в качестве регрессионной модели) или даже сложную имитационную модель и бросить их все вместе в яму оптимизации.

Если у вас есть какие-либо вопросы или идеи для обмена, пожалуйста, свяжитесь с автором по адресу tirthajyoti [AT] gmail.com, Также вы можете проверить автора GitHub хранилищадля других забавных фрагментов кода в Python, R или MATLAB и ресурсов машинного обучения. Если вы, как и я, увлечены машинным обучением / наукой о данных, пожалуйста, не стесняйтесь добавь меня в LinkedIn или Подпишись на меня в Твиттере.

Источник

Поиск минимума#

Подмодуль scipy.optimize содержит в себе множество методов для решения задач оптимизации (минимизация, максимизация).

from matplotlib import pyplot as plt def configure_matplotlib(): plt.rc('text', usetex=True) plt.rcParams["axes.titlesize"] = 28 plt.rcParams["axes.labelsize"] = 24 plt.rcParams["legend.fontsize"] = 24 plt.rcParams["xtick.labelsize"] = plt.rcParams["ytick.labelsize"] = 18 plt.rcParams["text.latex.preamble"] = r""" \usepackage[utf8]  \usepackage[english,russian]  \usepackage  """ configure_matplotlib() 

Минимизация скалярной функции одного аргумента#

Функция scipy.optimize.minimize_scalar ищет минимум функции \(f\colon \mathbb \to \mathbb\) при независимой переменной в области \(D\subset\mathbb\) , т.е. решает задачу

иными словами задачу поиска \(x^*\in\mathbb\) , такого что

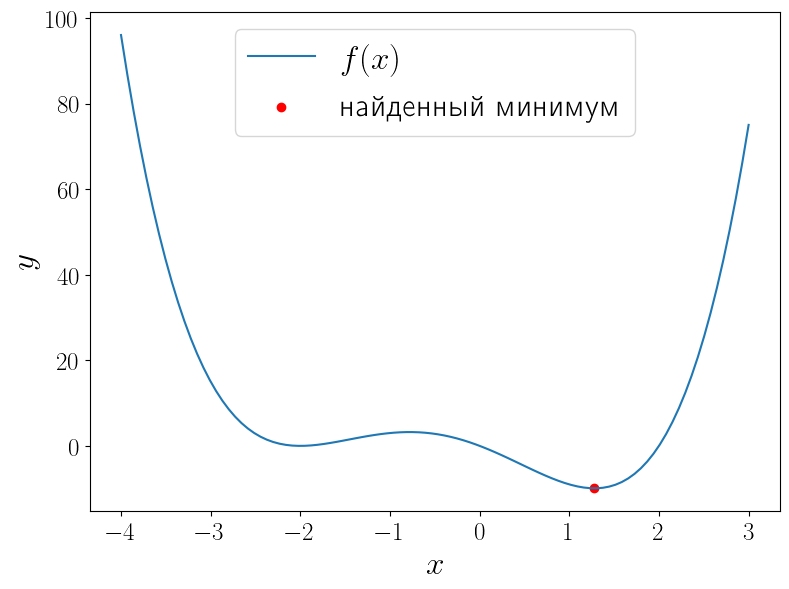
import numpy as np from scipy import optimize from matplotlib import pyplot as plt def f(x): return (x - 2) * x * (x + 2)**2 solution = optimize.minimize_scalar(f) print(solution) x = np.linspace(-4, 3, 100) fig, ax = plt.subplots(figsize=(8, 6), layout="tight") ax.plot(x, f(x), label=r"$f(x)$") ax.scatter(solution.x, solution.fun, color="red", label="найденный минимум") ax.set_xlabel("$x$") ax.set_ylabel("$y$") ax.legend() 

fun: -9.914949590828147 message: '\nOptimization terminated successfully;\nThe returned value satisfies the termination criteria\n(using xtol = 1.48e-08 )' nfev: 15 nit: 11 success: True x: 1.2807764040333458

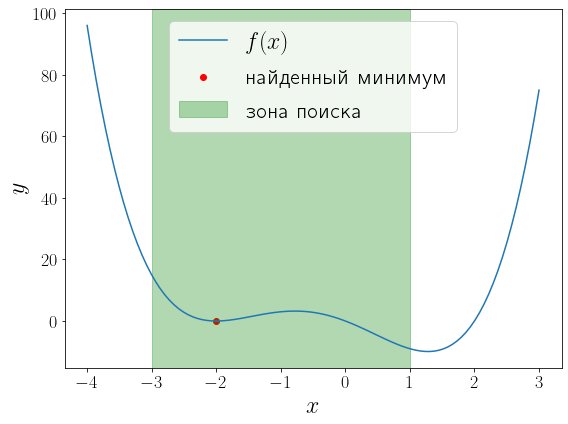
У функции \(f(x) = (x — 1)x(x + 2)^2\) два локальных минимума и функция minimize_scalar вернула из них глобальный. Можно сузить поиск область поиска минимума используя метод bounded .

a, b = -3, 1 solution = optimize.minimize_scalar(f, bounds=(a, b), method="bounded") fig, ax = plt.subplots(figsize=(8, 6), layout="tight") ax.plot(x, f(x), label="$f(x)$") ax.scatter(solution.x, solution.fun, color="red", label="найденный минимум") ax.set_xlabel("$x$") ax.set_ylabel("$y$") ax.axvspan(a, b, color="green", alpha=0.3, label="зона поиска") ax.legend() 

Минимизация функции многих переменных#

Общий случай#

Функция scipy.optimize.minimize предназначена для минимизации функции многих переменных \(f\colon\mathbb^n\to\mathbb\) при независимой переменной в области \(D\subset\mathbb^n\) :

При этом важно определить минимизируемую функцию именно принимающей один векторный аргумент, а не \(n\) скалярных.

В качестве примера рассмотрим поиск минимума функции Розенброка

Её минимум равен 0, который достигается при \(\alpha = \beta = 1\) . Для минимизации функции средствами SciPy необходимо определить её в виде функции одного векторного аргумента. Например, если положить, что \(\vec=\beginx_1 \\ x_2\end=\begin\alpha \\ \beta\end\) , то функцию Розенброка можно записать в виде

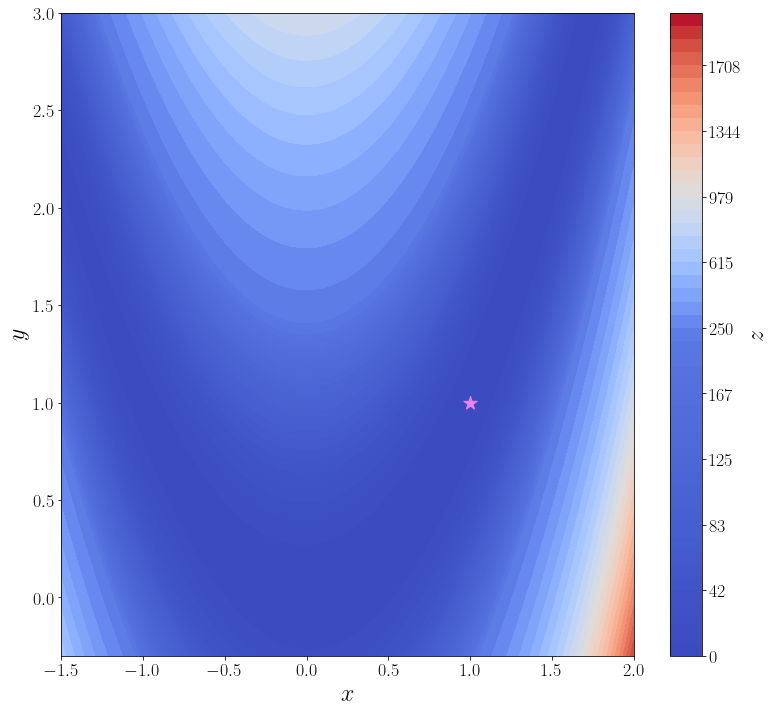
Именно в таком виде она уже определена в SciPy : rosen. Кроме того в SciPy доступны её градиент rosen_der и матрица Гессе rosen_hess. В ячейке ниже строится график этой функции.

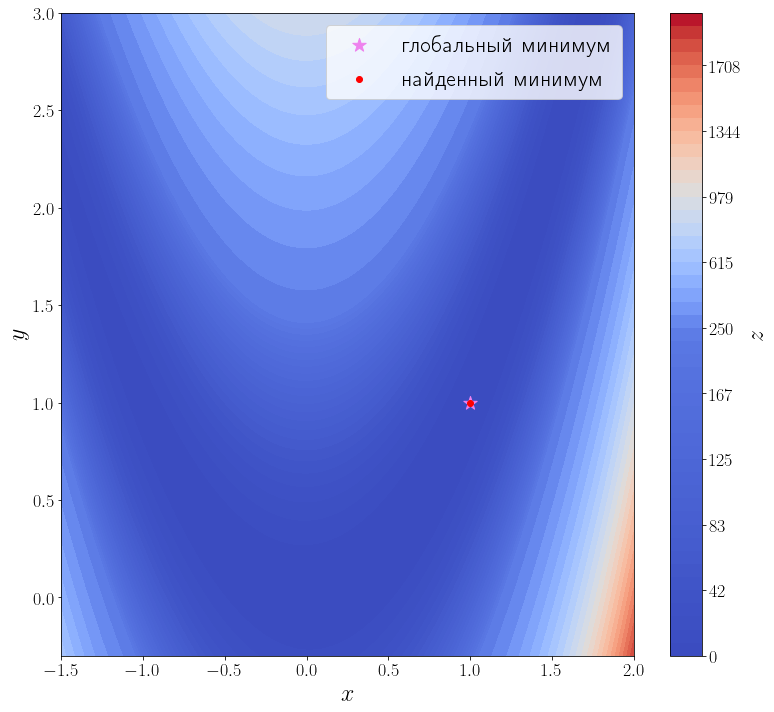
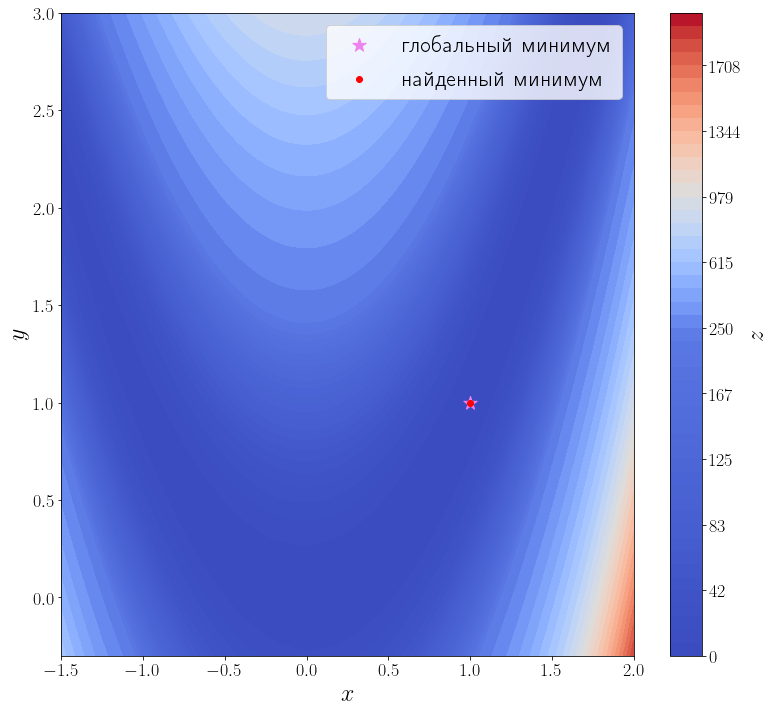
import numpy as np from scipy import optimize from matplotlib import pyplot as plt f = optimize.rosen def plot_surface(): n_points = 100 x = np.linspace(-1.5, 2.0, n_points) y = np.linspace(-0.3, 3, n_points) xx, yy = np.meshgrid(x, y) X = np.vstack([xx.flatten(), yy.flatten()]) zz = f(X).reshape(n_points, n_points) levels = np.hstack([np.linspace(0, 200, 25), np.linspace(250, 2000, 25)]) fig, ax = plt.subplots(figsize=(11, 10), layout="tight") cf = ax.contourf(xx, yy, zz, levels=levels, cmap="coolwarm") cbar = fig.colorbar(cf) ax.set_xlabel("$x$") ax.set_ylabel("$y$") cbar.set_label("$z$") ax.scatter([1], [1], marker="*", s=200, color="violet", label="глобальный минимум") return ax plot_surface() 

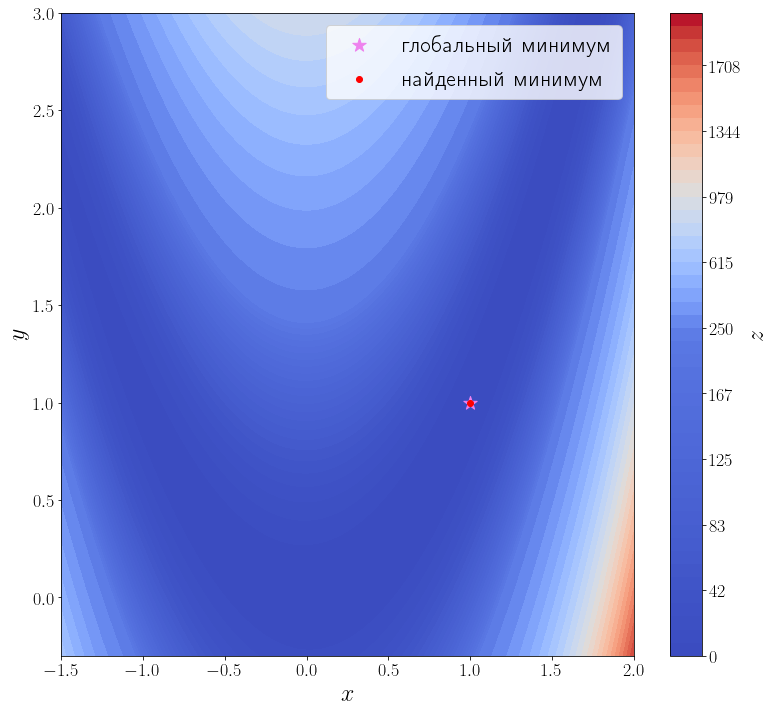
В самой простой своей форме достаточно передать методу optimize.minimize минимизируемую функцию \(f\) и начальное приближение \(x_0\) .

solution = optimize.minimize(f, x0=[3, 0]) print(solution) ax = plot_surface() ax.scatter(solution.x[0], solution.x[1], color="red", label="найденный минимум") ax.legend() 

fun: 2.0042284826789698e-11 hess_inv: array([[0.49906269, 0.99813029], [0.99813029, 2.00126989]]) jac: array([-2.75307058e-08, 1.52773794e-08]) message: 'Optimization terminated successfully.' nfev: 168 nit: 42 njev: 56 status: 0 success: True x: array([0.99999552, 0.99999104])

Из возвращаемого значения видно, что метод успешно сошелся и алгоритму потребовалось 42 итерации и 168 вызовов функции f , чтобы сойтись.

Известна первая производная#

Передадим этому методу функцию, вычисляющую матрицу градиент искомой функции. Для этого необходимо использовать параметр jac этой функции.

jacobian = optimize.rosen_der solution = optimize.minimize(f, x0=[3, 0], jac=jacobian) print(solution) ax = plot_surface() ax.scatter(solution.x[0], solution.x[1], color="red", label="найденный минимум") ax.legend() 

fun: 1.0497719786985556e-20 hess_inv: array([[0.49999817, 1.00001013], [1.00001013, 2.00505181]]) jac: array([-2.72340728e-09, 1.43485224e-09]) message: 'Optimization terminated successfully.' nfev: 54 nit: 42 njev: 54 status: 0 success: True x: array([1., 1.])

Количество итераций осталось прежним, а количество вызовов функции f снизилось до 35. Это достигается за счет того, что метод минимизации вычисляет производную, вызывая переданную функцию jac , а до этого он её оценивал численно, что требовало дополнительных вызовов f .

Известны первая и вторая производные#

Передадим ещё информацию о второй производной функции f , т.е. матрицу Гессе. Метод минимизации по умолчанию ( BFGS ) — метод первого порядка, чтобы задействовать матрицу Гессе, необходимо использовать метод второго порядка, например, dogleg .

hessian = optimize.rosen_hess solution = optimize.minimize(f, [3, 0], method="dogleg", jac=jacobian, hess=hessian) print(solution) ax = plot_surface() ax.scatter(solution.x[0], solution.x[1], color="red", label="найденный минимум") ax.legend() 

fun: 3.514212495812258e-16 hess: array([[ 802.00002985, -400.00000744], [-400.00000744, 200. ]]) jac: array([ 1.31311361e-07, -4.70576911e-08]) message: 'Optimization terminated successfully.' nfev: 18 nhev: 14 nit: 17 njev: 15 status: 0 success: True x: array([1.00000002, 1.00000004])

Методу второго порядка потребовалось всего 17 итераций и 18 вызовов функции f , чтобы сойтись.

Дифференцирование и интегрирование функций

Решение нелинейных уравнений

By Fadeev Egor
© Copyright 2022.

Источник