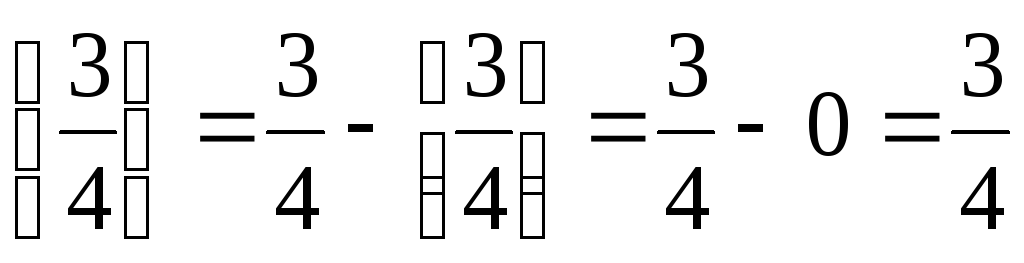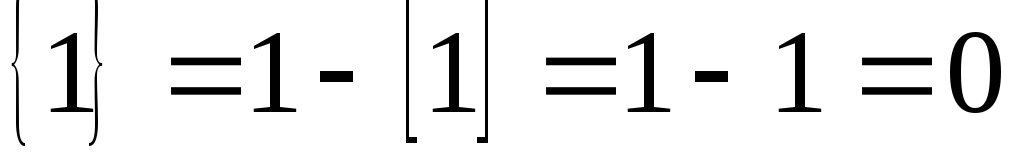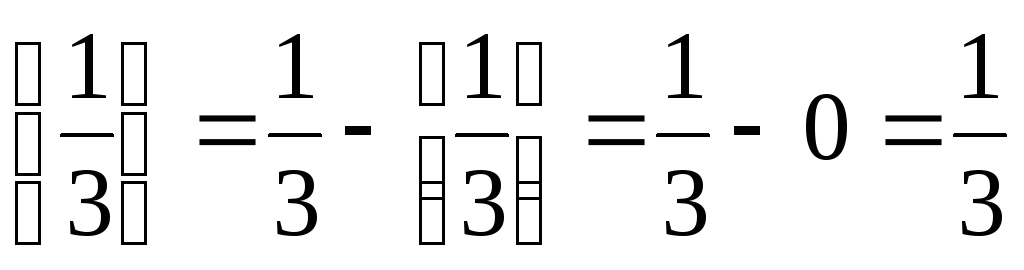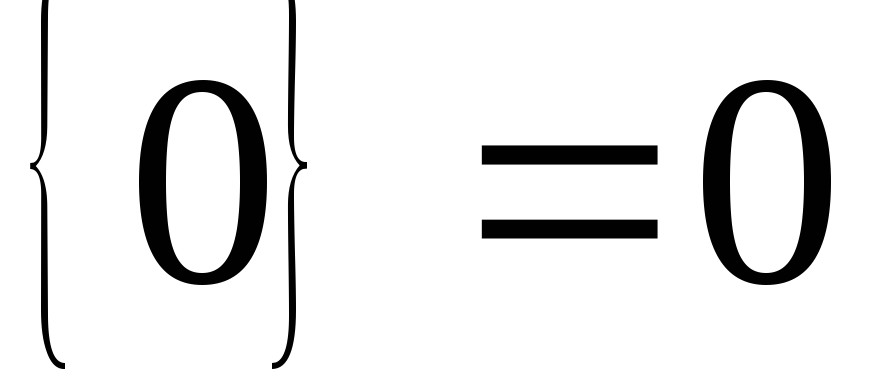Метод Гомори
Метод Гомори решения задач целочисленного программирования является методом отсечения.
Суть метода заключается в построении ограничений, отсекающих нецелочисленные решения задачи линейного программирования, но не отсекающих ни одного целочисленного плана. Для этого сначала решается ослабленная задача линейного программирования без учета условия целочисленности переменных.
Если полученное решение задачи линейного программирования является целочисленным, то задача целочисленного программирования также решена и найденное решение является оптимальным и для нее. Если же в найденном решении задачи линейного программирования одна или большее число переменных не целые, то для отыскания целочисленного решения задачи добавляются новое линейное ограничение, которое отсекает нецелочисленные решения. При продолжении решения расширенной задачи двойственным симплексным методом с учетом этого ограничения получается целочисленный план.
Для нахождения целочисленного решения задачи методом Гомори используется следующий алгоритм.
- Решаем ослабленную задачу симплексным методом без учета условия целочисленности. Если все компоненты оптимального плана целые, то он является оптимальным и для задачи целочисленного программирования. Если обнаруживается неразрешимость задачи, то и неразрешима задача целочисленного программирования.
- Если в результате решения задачи линейного программирования в полученном оптимальном плане
есть нецелая базисная переменная
, то к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами:
— оно должно быть линейным; — должно отсекать найденный оптимальный нецелочисленный план; — не должно отсекать ни одного целочисленного плана. Если нецелых базисных переменных несколько, то для составления ограничения выбираем компоненту оптимального плана 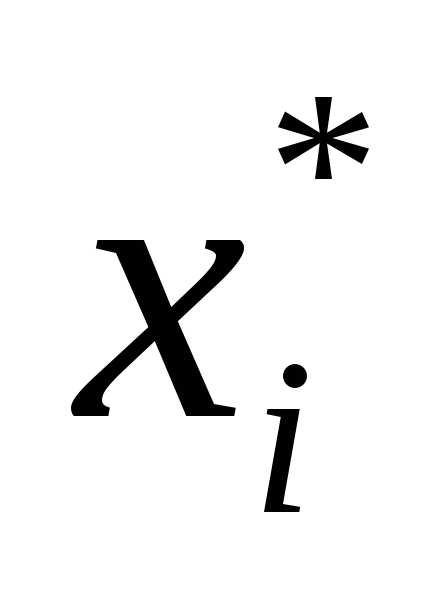

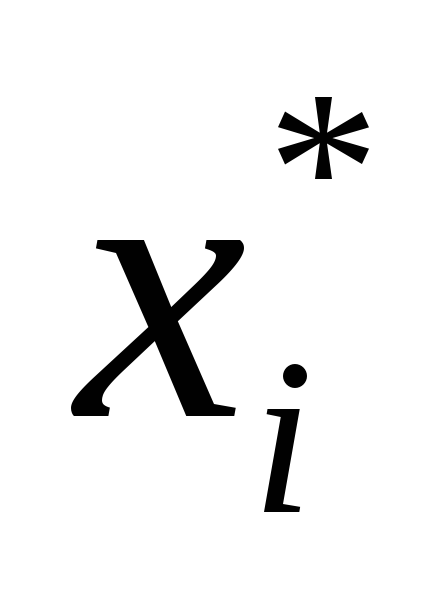








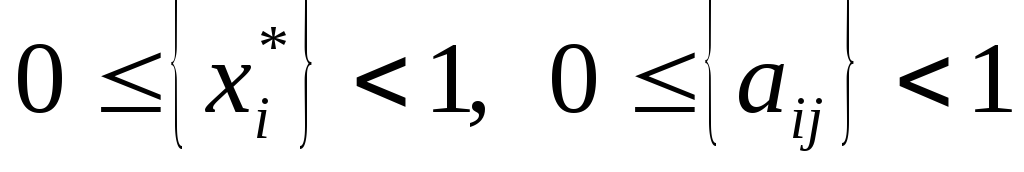
- Составляем неравенство Гомори
и включаем его в систему ограничений исходной задачи.
Для этого по производящей строке симплексной таблицы выписывается уравнение, предполагая, что первые m переменных являются базисными для данного оптимального плана 

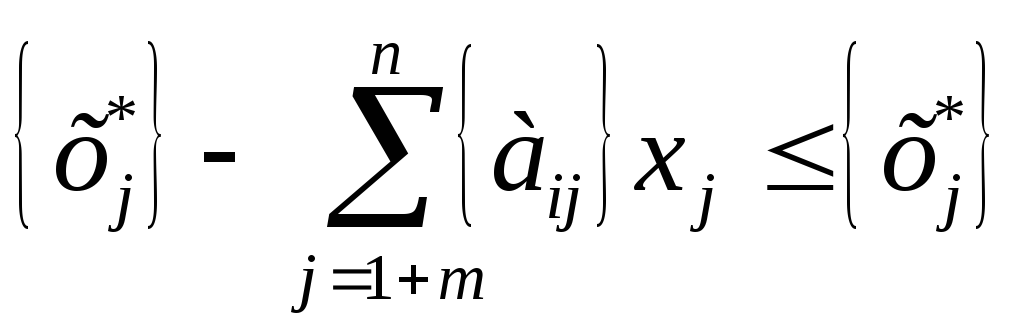


- Неравенство преобразуется в уравнение путем введения дополнительной неотрицательной переменной и включается в оптимальную симплексную таблицу.
- Решаем задачу, используя двойственный симплексный метод. Если новый оптимальный план расширенной задачи будет целочисленным, то задача решена. Если же решение нецелое, то нужно повторять алгоритм метода Гомори вплоть до получения целочисленного решения.
Пример. Методом Гомори найти решение задачи целочисленного программирования, состоящей в определении максимального значения функции 


| Б | СБ | В | С1=5 | С2=11 | С3=0 | С4=0 |
| а1 | а2 | а3 | а4 | |||
| а3 | 0 |  | 3 | 4 | 1 | 0 |
| а4 | 0 | 10 | 2 | 5 | 0 | 1 |
| ∆j=Zj–Сj | 0 | -5 | -11 | 0 | 0 | |
| СБ | В | С1=5 | С2=11 | С3=0 | С4=0 | |
| а1 | а2 | а3 | а4 | |||
| а2 | 11 |  |  | 1 |  | 0 |
| а4 | 0 | 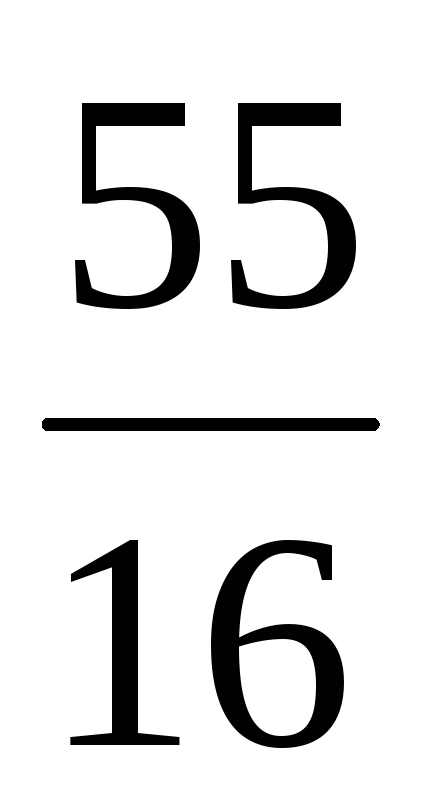 |  | 0 |  | 1 |
| ∆j=Zj–Сj |  |  | 0 | 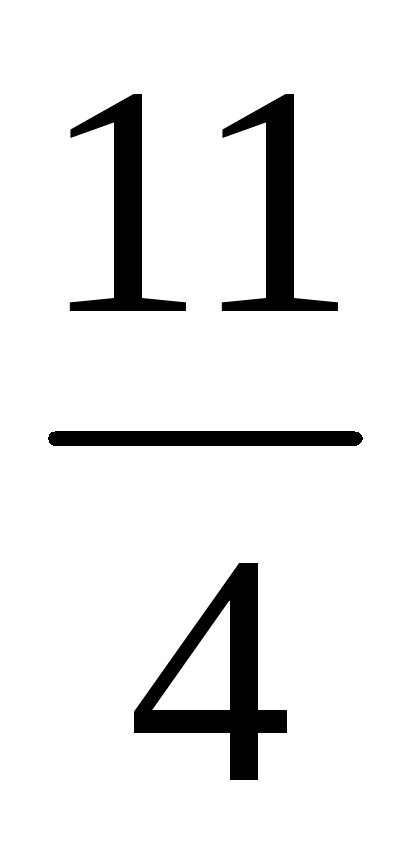 | 0 | |
В найденном оптимальном плане значение переменной х2 равно дробному числу. Находим его дробную часть и дробные части всех элементов строки, содержащей переменную х2 , а именно: 


| Б | СБ | В | С1=5 | С2=11 | С3=0 | С4=0 | С5=0 |
| а1 | а2 | а3 | а4 | а5 | |||
| а2 | 110 | 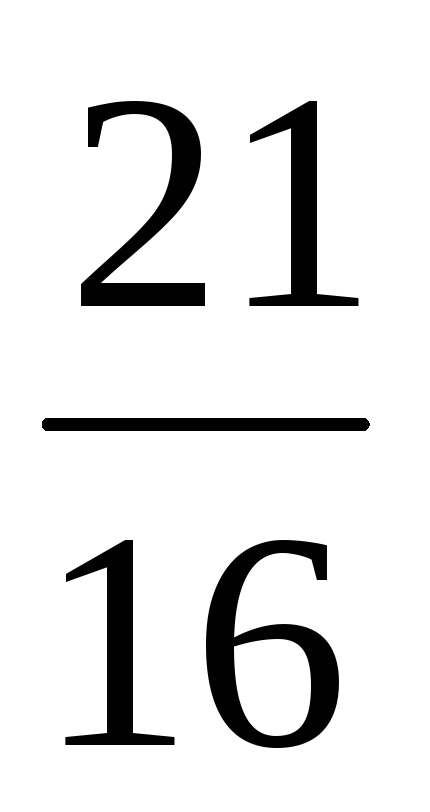 |  | 1 | 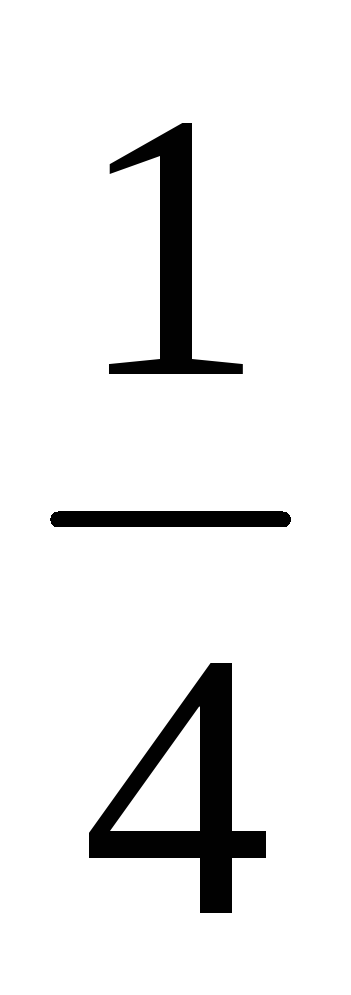 | 0 | 0 |
| а4 | 0 |  |  | 0 |  | 1 | 0 |
| а5 | 0 |  |  | 0 |  | 0 | 1 |
| ∆j =Zj–Сj |  | 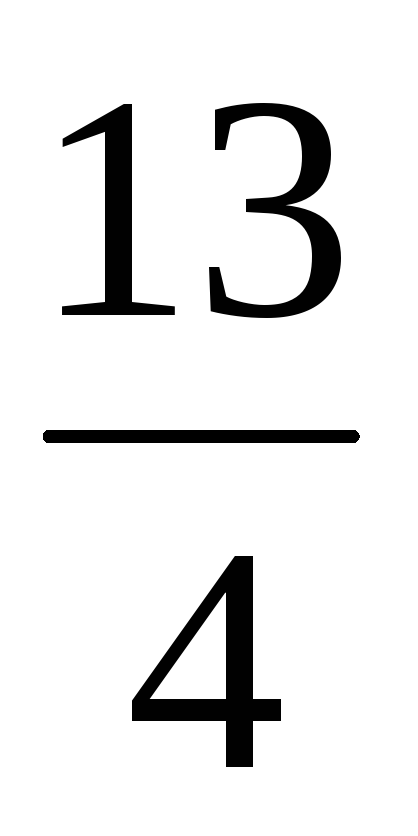 | 0 | 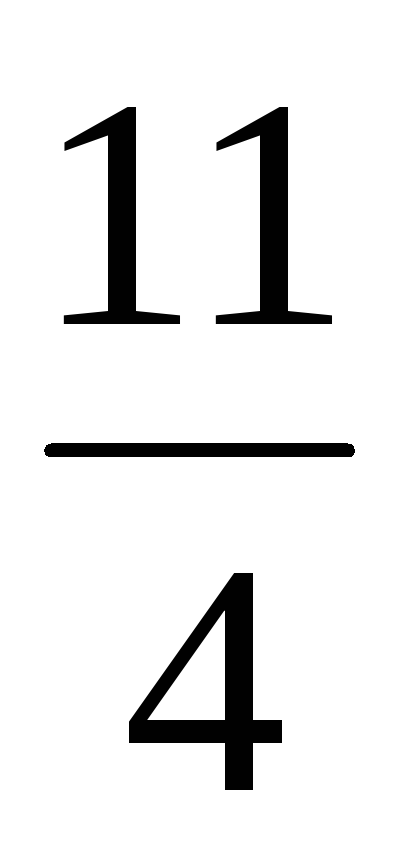 | 0 | 0 | |
| Б | СБ | В | С1=5 | С2=11 | С3=0 | С4=0 | С5=0 |
| а1 | а2 | а3 | а4 | а5 | |||
| а2 | 11 | 1 | 0 | 1 | 0 | 0 | 1 |
| а4 | 0 |  | 0 | 0 | 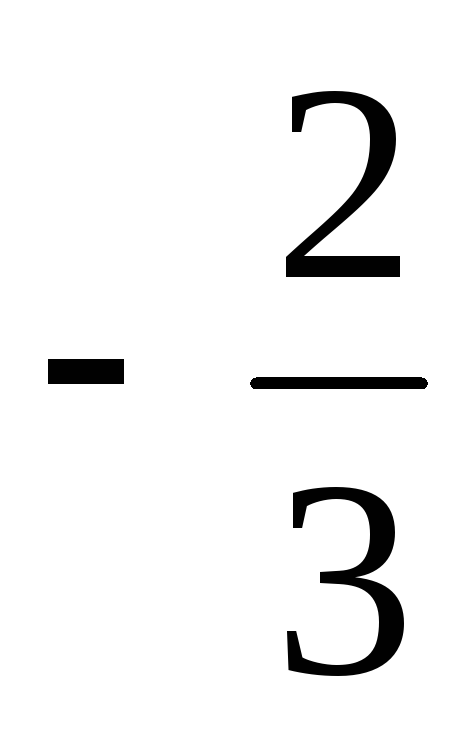 | 1 |  |
| а1 | 0 | 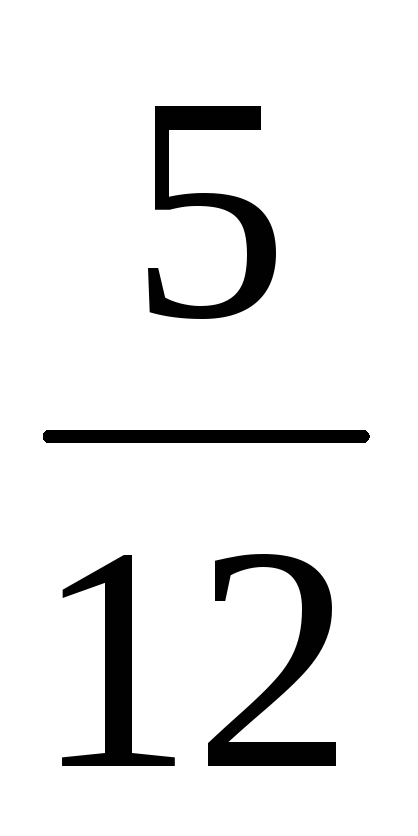 | 1 | 0 |  | 0 | 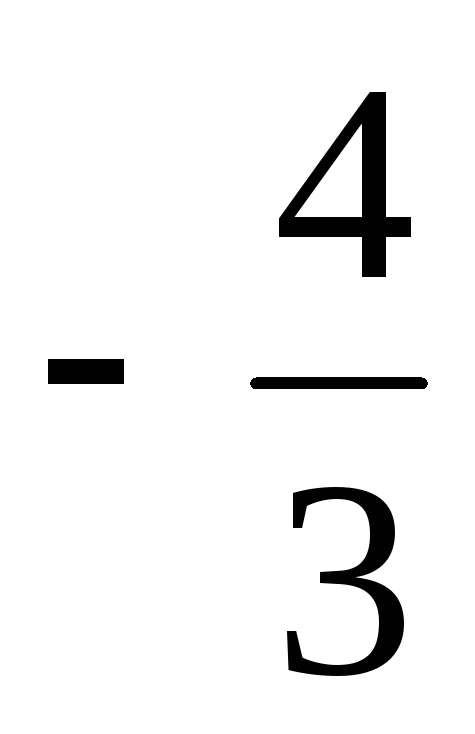 |
| ∆j =Zj–Сj |  | 0 | 0 | 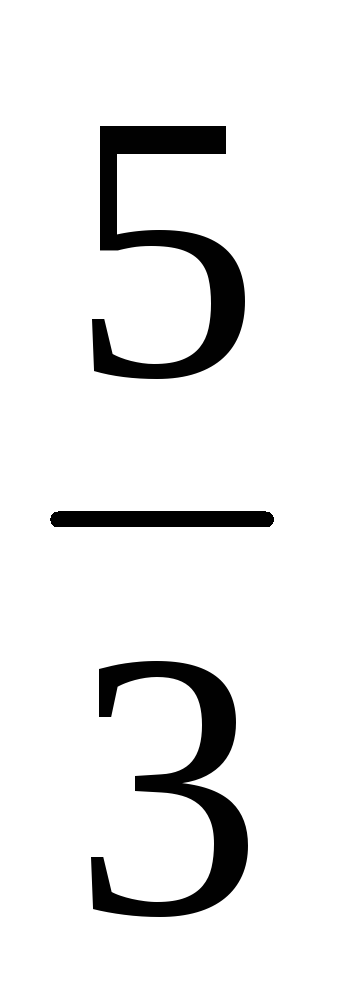 | 0 |  | |
Полученное оптимальное решение расширенной задачи содержит нецелое значение переменной х1, поэтому находим для этой строки дробные части всех нецелых чисел, а именно: 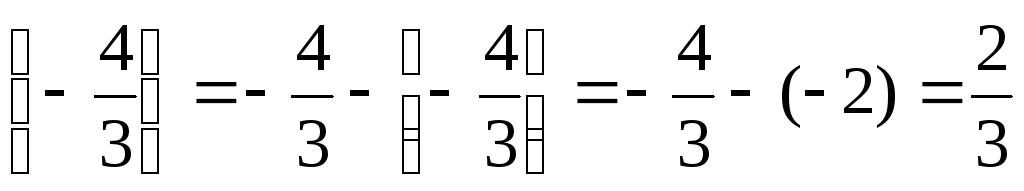
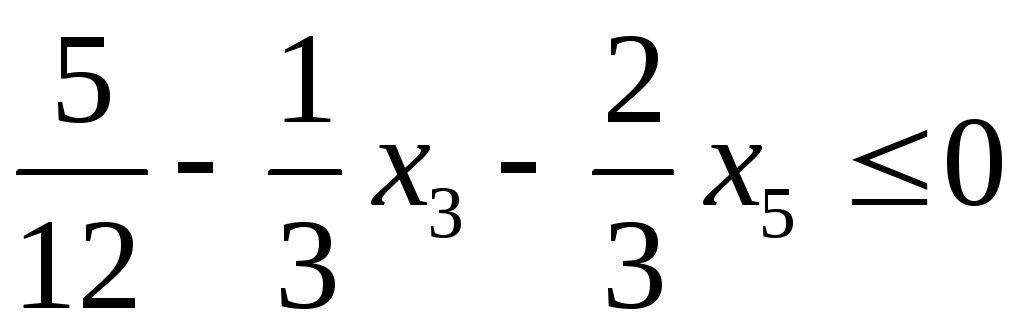

| Б | СБ | В | С1=5 | С2=11 | С3=0 | С4=0 | С5=0 | С6=0 |
| а1 | а2 | а3 | а4 | а5 | а6 | |||
| а2 | 110 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| а4 | 0 | 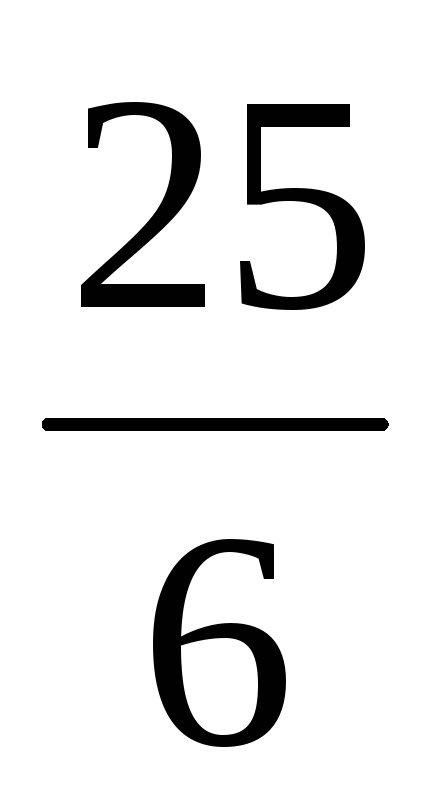 | 0 | 0 |  | 1 |  | 0 |
| а1 | 0 |  | 1 | 0 |  | 0 | 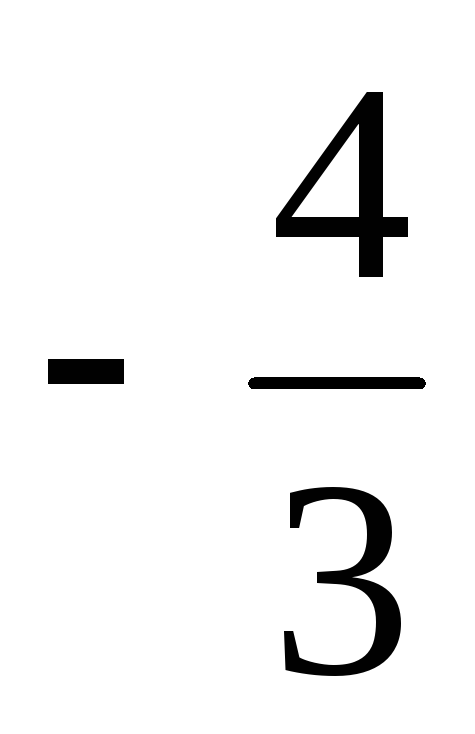 | 0 |
| а6 | 0 |  | 0 | 0 |  | 0 |  | 1 |
| ∆j =Zj–Сj |  | 0 | 0 |  | 0 |  | 0 | |
| Б | СБ | В | С1=5 | С2=11 | С3=0 | С4=0 | С5=0 | С6=0 |
| а1 | а2 | а3 | а4 | а5 | а6 | |||
| а2 | 110 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| а4 | 0 | 5 | 0 | 0 | 0 | 1 | -1 | -2 |
| а1 | 0 | 0 | 1 | 0 | 0 | 0 | -2 | 1 |
| а3 | 0 |  | 0 | 0 | 1 | 0 | 2 | -3 |
| ∆j =Zj–Сj | 11 | 0 | 0 | 0 | 0 | 1 | 5 | |
Таким образом, найдено оптимальное решение задачи целочисленного программирования: Zmax =11 при 
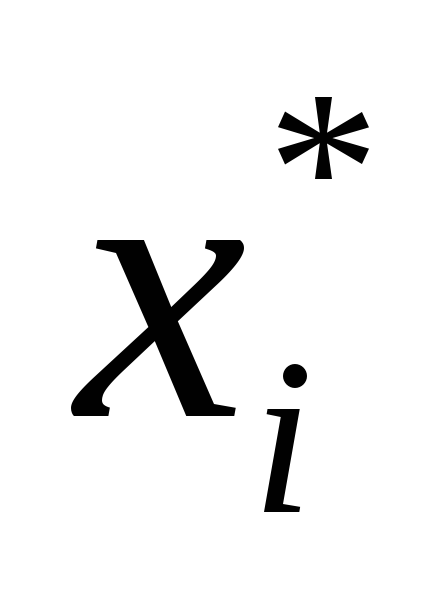
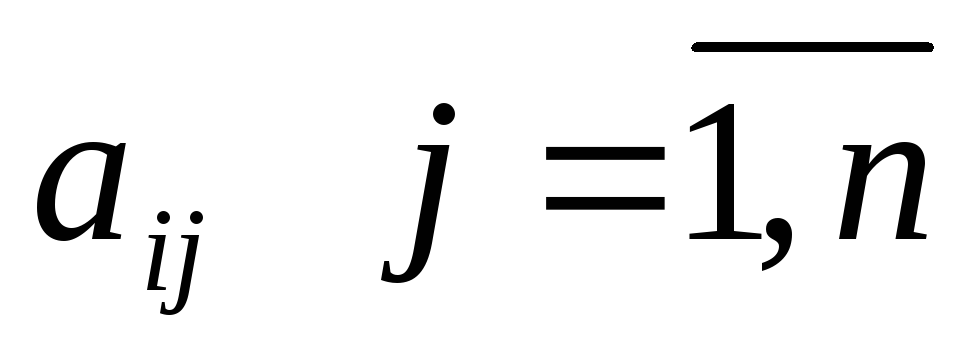
 есть нецелая базисная переменная
есть нецелая базисная переменная , то к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами:
, то к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами:
 и включаем его в систему ограничений исходной задачи.
и включаем его в систему ограничений исходной задачи.