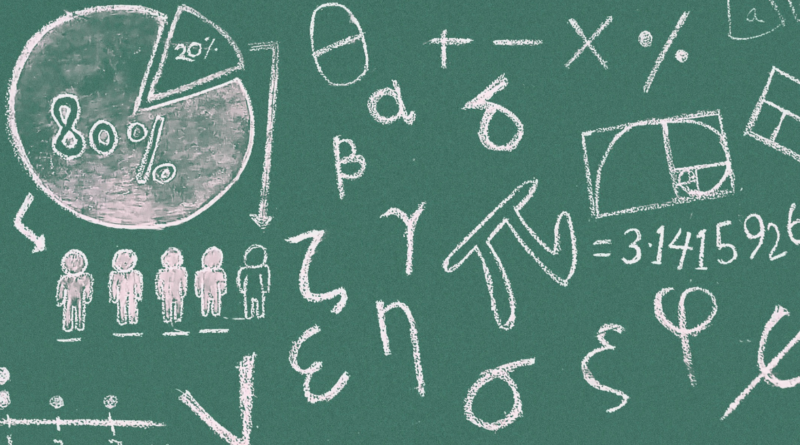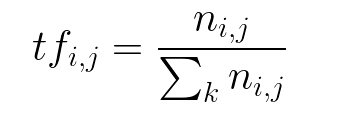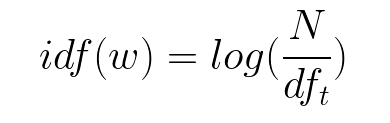Метод tf idf python

Understanding TF-IDF with Python example

Term Frequency – Inverse Document Frequency (TF-IDF) is a popular statistical technique utilized in natural language processing and information retrieval to assess a term’s significance in a document in comparison to a group of documents, known as a corpus. The technique employs a text vectorization process to transform words in a text document into numerical values that denote their importance. Various scoring methods exist for text vectorization, with TF-IDF being among the most prevalent. As its name implies, TF-IDF vectorizes/scores a word by multiplying the word’s Term Frequency (TF) with the Inverse Document Frequency (IDF). You can find the codes of this post on my Github.

Term Frequency: TF of a term or word is the number of times the term appears in a document compared to the total number of words in the document.

Inverse Document Frequency: IDF of a term reflects the proportion of documents in the corpus that contain the term. Words unique to a small percentage of documents (e.g., technical jargon terms) receive higher importance values than words common across all documents (e.g., a, the, and).

The TF-IDF of a term is calculated by multiplying TF and IDF scores.

Translated into plain English, the importance of a term is high when it occurs a lot in a given document and rarely in others. In short, commonality within a document measured by TF is balanced by rarity between documents measured by IDF. The resulting TF-IDF score reflects the importance of a term for a document in the corpus.

TF-IDF is useful in many natural language processing applications. For example, Search Engines use TF-IDF to rank the relevance of a document for a query. TF-IDF is also employed in text classification, text summarization, and topic modeling.

Note that there are some different approaches to calculating the IDF score. The base 10 logarithm is often used in the calculation. However, some libraries use a natural logarithm. In addition, one can be added to the denominator as follows in order to avoid division by zero.

Numerical Example

Imagine the term t appears 20 times in a document that contains a total of 100 words. The Term Frequency (TF) of t can be calculated as follow:

Assume a collection of related documents containing 10,000 documents. If 100 documents out of 10,000 documents contain the term t, the Inverse Document Frequency (IDF) of t can be calculated as follows

Using these two quantities, we can calculate the TF-IDF score of the term t for the document.

Python Implementation

Some popular python libraries have a function to calculate TF-IDF. The popular machine learning library Sklearn has TfidfVectorizer() function (docs).

We will write a TF-IDF function from scratch using the standard formula given above, but we will not apply any preprocessing operations such as stop words removal, stemming, punctuation removal, or lowercasing. It should be noted that the result may be different when using a native function built into a library.

import pandas as pd import numpy as np

First, let’s construct a small corpus.

corpus = ['data science is one of the most important fields of science', 'this is one of the best data science courses', 'data scientists analyze data' ]

Next, we’ll create a word set for the corpus:

words_set = set() for doc in corpus: words = doc.split(' ') words_set = words_set.union(set(words)) print('Number of words in the corpus:',len(words_set)) print('The words in the corpus: \n', words_set)

Number of words in the corpus: 14 The words in the corpus:

Computing Term Frequency

Now we can create a dataframe by the number of documents in the corpus and the word set, and use that information to compute the term frequency (TF):

n_docs = len(corpus) #·Number of documents in the corpus n_words_set = len(words_set) #·Number of unique words in the df_tf = pd.DataFrame(np.zeros((n_docs, n_words_set)), columns=words_set) # Compute Term Frequency (TF) for i in range(n_docs): words = corpus[i].split(' ') # Words in the document for w in words: df_tf[w][i] = df_tf[w][i] + (1 / len(words)) df_tf

The dataframe above shows we have a column for each word and a row for each document. This shows the frequency of each word in each document.

Computing Inverse Document Frequency

Now, we’ll compute the inverse document frequency (IDF):

print("IDF of: ") idf = <> for w in words_set: k = 0 # number of documents in the corpus that contain this word for i in range(n_docs): if w in corpus[i].split(): k += 1 idf[w] = np.log10(n_docs / k) print(f'15>: 10>' )

IDF of: important: 0.47712125471966244 scientists: 0.47712125471966244 best: 0.47712125471966244 courses: 0.47712125471966244 this: 0.47712125471966244 analyze: 0.47712125471966244 of: 0.17609125905568124 most: 0.47712125471966244 the: 0.17609125905568124 is: 0.17609125905568124 science: 0.17609125905568124 fields: 0.47712125471966244 one: 0.17609125905568124 data: 0.0

Putting it Together: Computing TF-IDF

Since we have TF and IDF now, we can compute TF-IDF:

df_tf_idf = df_tf.copy() for w in words_set: for i in range(n_docs): df_tf_idf[w][i] = df_tf[w][i] * idf[w] df_tf_idf

Notice that “data” has an IDF of 0 because it appears in every document. As a result, “is” is not considered to be an important term in this corpus. This will change slightly in the following sklearn implementation, where “data” will be non-zero.

TF-IDF Using scikit-learn

First, we need to import sklearn TfidfVectorizer:

from sklearn.feature_extraction.text import TfidfVectorizer

We need to instantiate the class first, then we can call the fit_transform method on our test corpus. This will perform all of the calculations we performed above.

tr_idf_model = TfidfVectorizer() tf_idf_vector = tr_idf_model.fit_transform(corpus)

After vectorizing the corpus by the function, a sparse matrix is obtained.

Here’s the current shape of the matrix:

print(type(tf_idf_vector), tf_idf_vector.shape) # (3,14)

And we can convert to a regular array to get a better idea of the values:

tf_idf_array = tf_idf_vector.toarray() print(tf_idf_array)

[[0. 0. 0. 0.18952581 0.32089509 0.32089509 0.24404899 0.32089509 0.48809797 0.24404899 0.48809797 0. 0.24404899 0. ] [0. 0.40029393 0.40029393 0.23642005 0. 0. 0.30443385 0. 0.30443385 0.30443385 0.30443385 0. 0.30443385 0.40029393] [0.54270061 0. 0. 0.64105545 0. 0. 0. 0. 0. 0. 0. 0.54270061 0. 0. ]]

It’s now very straightforward to obtain the original terms in the corpus by using get_feature_names _out:

words_set = tr_idf_model.get_feature_names_out() print(words_set)

['analyze', 'best', 'courses', 'data', 'fields', 'important', 'is', 'most', 'of', 'one', 'science', 'scientists', 'the', 'this']

Finally, we’ll create a dataframe to better show the TF-IDF scores of each document:

df_tf_idf = pd.DataFrame(tf_idf_array, columns = words_set) df_tf_idf

As you can see from the output above, the TF-IDF scores are different than the scores obtained by the manual process we used earlier. This difference is due to the sklearn implementation of TF-IDF, which uses a slightly different formula. For more details, you can learn more about how sklearn calculates TF-IDF term weighting here.

Источник

How to process textual data using TF-IDF in Python

Computers are good with numbers, but not that much with textual data. One of the most widely used techniques to process textual data is TF-IDF. In this article, we will learn how it works and what are its features.

From our intuition, we think that the words which appear more often should have a greater weight in textual data analysis, but that’s not always the case. Words such as “the”, “will”, and “you” — called stopwords — appear the most in a corpus of text, but are of very little significance. Instead, the words which are rare are the ones that actually help in distinguishing between the data, and carry more weight.

An introduction to TF-IDF

TF-IDF stands for “Term Frequency — Inverse Data Frequency”. First, we will learn what this term means mathematically.

Term Frequency (tf): gives us the frequency of the word in each document in the corpus. It is the ratio of number of times the word appears in a document compared to the total number of words in that document. It increases as the number of occurrences of that word within the document increases. Each document has its own tf.

Inverse Data Frequency (idf): used to calculate the weight of rare words across all documents in the corpus. The words that occur rarely in the corpus have a high IDF score. It is given by the equation below.

Combining these two we come up with the TF-IDF score (w) for a word in a document in the corpus. It is the product of tf and idf:

Let’s take an example to get a clearer understanding.

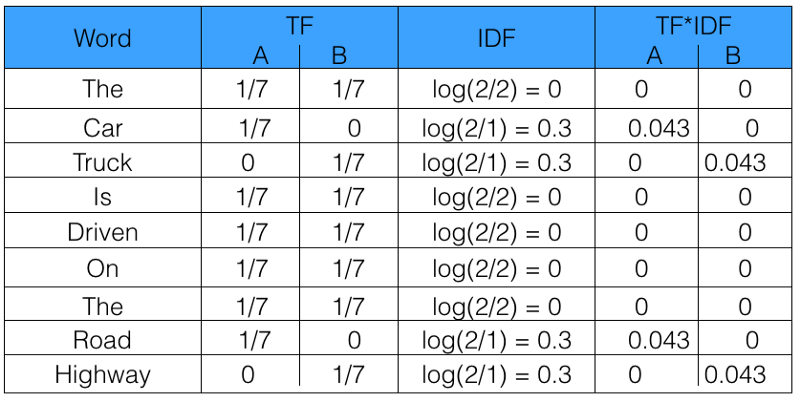
Sentence 1 : The car is driven on the road.

Sentence 2: The truck is driven on the highway.

In this example, each sentence is a separate document.

We will now calculate the TF-IDF for the above two documents, which represent our corpus.

From the above table, we can see that TF-IDF of common words was zero, which shows they are not significant. On the other hand, the TF-IDF of “car” , “truck”, “road”, and “highway” are non-zero. These words have more significance.

Using Python to calculate TF-IDF

Lets now code TF-IDF in Python from scratch. After that, we will see how we can use sklearn to automate the process.

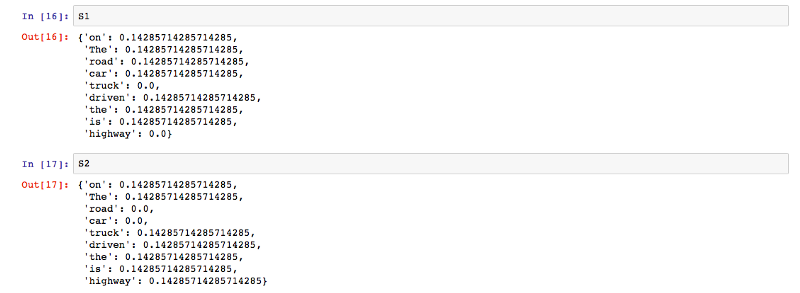
The function computeTF computes the TF score for each word in the corpus, by document.

The function computeIDF computes the IDF score of every word in the corpus.

The function computeTFIDF below computes the TF-IDF score for each word, by multiplying the TF and IDF scores.

The output produced by the above code for the set of documents D1 and D2 is the same as what we manually calculated above in the table.

You can refer to this link for the complete implementation.

sklearn

Now we will see how we can implement this using sklearn in Python.

First, we will import TfidfVectorizer from sklearn.feature_extraction.text :

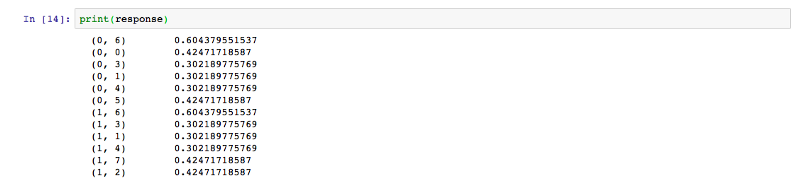
Now we will initialise the vectorizer and then call fit and transform over it to calculate the TF-IDF score for the text.

Under the hood, the sklearn fit_transform executes the following fit and transform functions. These can be found in the official sklearn library at GitHub.

 def fit(self, X, y=None): """Learn the idf vector (global term weights) Parameters ---------- X : sparse matrix, [n_samples, n_features] a matrix of term/token counts """ if not sp.issparse(X): X = sp.csc_matrix(X) if self.use_idf: n_samples, n_features = X.shape df = _document_frequency(X) # perform idf smoothing if required df += int(self.smooth_idf) n_samples += int(self.smooth_idf) # log+1 instead of log makes sure terms with zero idf don't get # suppressed entirely. idf = np.log(float(n_samples) / df) + 1.0 self._idf_diag = sp.spdiags(idf, diags=0, m=n_features, n=n_features, format='csr') return self def transform(self, X, copy=True): """Transform a count matrix to a tf or tf-idf representation Parameters ---------- X : sparse matrix, [n_samples, n_features] a matrix of term/token counts copy : boolean, default True Whether to copy X and operate on the copy or perform in-place operations. Returns ------- vectors : sparse matrix, [n_samples, n_features] """ if hasattr(X, 'dtype') and np.issubdtype(X.dtype, np.floating): # preserve float family dtype X = sp.csr_matrix(X, copy=copy) else: # convert counts or binary occurrences to floats X = sp.csr_matrix(X, dtype=np.float64, copy=copy) n_samples, n_features = X.shape if self.sublinear_tf: np.log(X.data, X.data) X.data += 1 if self.use_idf: check_is_fitted(self, '_idf_diag', 'idf vector is not fitted') expected_n_features = self._idf_diag.shape[0] if n_features != expected_n_features: raise ValueError("Input has n_features=%d while the model" " has been trained with n_features=%d" % ( n_features, expected_n_features)) # *= doesn't work X = X * self._idf_diag if self.norm: X = normalize(X, norm=self.norm, copy=False) return X

One thing to notice in the above code is that, instead of just the log of n_samples, 1 has been added to n_samples to calculate the IDF score. This ensures that the words with an IDF score of zero don’t get suppressed entirely.

The output obtained is in the form of a skewed matrix, which is normalised to get the following result.

Thus we saw how we can easily code TF-IDF in just 4 lines using sklearn. Now we understand how powerful TF-IDF is as a tool to process textual data out of a corpus. To learn more about sklearn TF-IDF, you can use this link.

Happy coding!

Thanks for reading this article. Be sure to share it if you find it helpful.

For more about programming, you can follow me, so that you get notified every time I come up with a new post.

Источник