- Лабораторные / АТПП-3-Лабораторные / Метод параллельного программирования
- Метод последовательного программирования
- Области применения методов программирования схем переменных состояния
- Аналитический способ получения матрицы перехода
- Получение матрицы перехода разложением в ряд
- Получение матрицы перехода по схеме переменных состояния
- Схемы переменных состояний (спс)
- Метод прямого программирования (базовый)
- Методы последовательного и параллельного программирования
- Схемы переменных состояния типовых звеньев
- 6.2. Способы построения схем переменных состояния
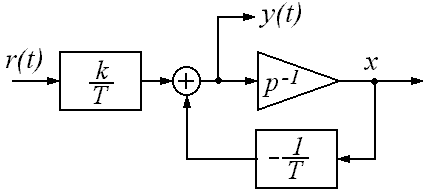
- Метод прямого программирования
- Метод параллельного программирования
- Метод последовательного программирования
- Описание сау методом пространства состояния
- Схемы переменных состояний (спс)
- Метод прямого программирования
- Метод параллельного программирования
Лабораторные / АТПП-3-Лабораторные / Метод параллельного программирования
Применяется, если
Пример:



Метод последовательного программирования
Применяется, когда САУ представлена структурной схемой с использованием типовых звеньев. В этом случае каждое из типовых звеньев заменяется соответствующей ему схеме переменных состояния, построенной методом прямого программирования.
П ример:
Области применения методов программирования схем переменных состояния
Если САУ представлена передаточной функцией высокого порядка и не раскладывается на простые составляющие, то применяется метод прямого программирования.
Если САУ представлена структурной схемой, в которой м.б. выделены типовые звенья, то применяется метод последовательного программирования, кроме того метод последовательного программирования применяется в том случае, если для использования САУ необходимы не только выходные, но и промежуточные переменный.
Схема переменных состояния построенная методом последовательного программирования имеет наиболее ясный физический смысл.
Схема переменных состояния, построенная методом параллельного программирования применяется тогда, когда W(p) представлена в виде типовых передаточных функций. В этом случае матрица коэффициентов имеет наиболее простой вид, сто облегчает дальнейшее исследование САУ
Матрицы перехода

Т – некоторое время (не постоянная времени)
Матрицу перехода можно получить тремя способами:
Аналитический способ получения матрицы перехода

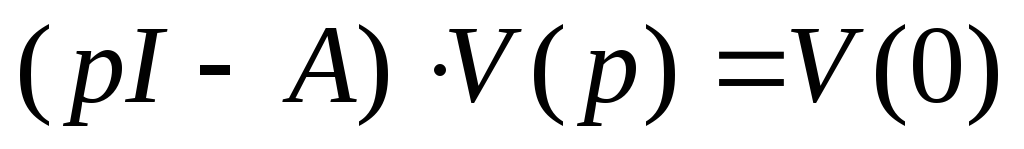




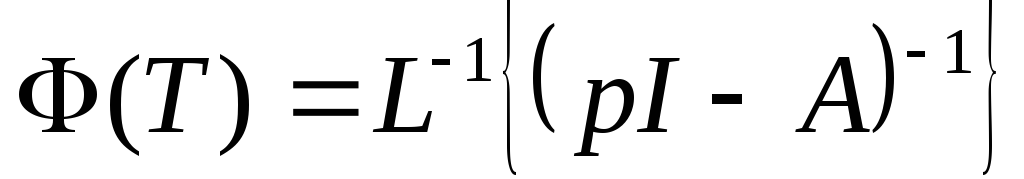





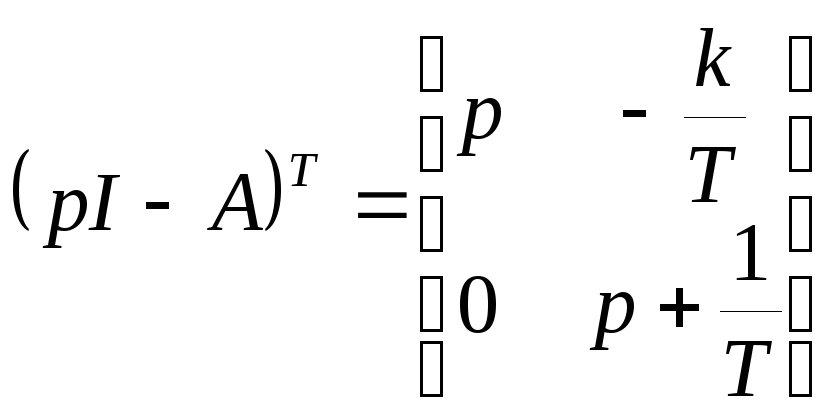

Получение матрицы перехода разложением в ряд
Решением дифференциального уравнения (1) является: 

Получение матрицы перехода по схеме переменных состояния





Схемы переменных состояний (спс)
Схемы переменных состояния состоят из следующих основных элементов:
- В основе СПС лежит единичный интегратор:
- Следующим основным элементом СПС является пропорциональное (безынерционное) звено:
- Сумматор.
Схемы переменных состояния строятся по передаточной функции объекта. Существует три способа построения схем состояния:
- метод прямого программирования (базовый);
- метод параллельного программирования;
- метод последовательного программирования.
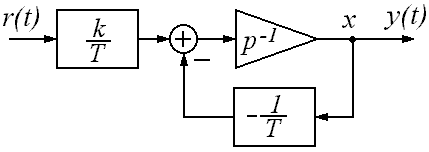
Метод прямого программирования (базовый)
Используется, если описание САУ представлено в виде передаточной функции: 
- Получаем преобразованную передаточную функцию: числитель и знаменатель исходной делим на
в наивысшей степени, (переходя тем самым к отрицательным степеням
), а также на коэффициентa0. СПС построить невозможно, если m > n.
- Строим последовательную цепь из k единичных интеграторов, где k — максимальный модуль степени рчислителя преобразованной передаточной функции.
- Числитель преобразованной передаточной функции позволяет построить прямые линии связи. Выход каждого (
того) интегратора умножается на соответствующий коэффициент (
), затем получившиеся сигналы суммируются. Если коэффициент (
) = 0, то это говорит об отсутствии соответствующего сигнала. Количество слагаемых числителя преобразованной передаточной функции равно количеству сигналов, образующих выходной сигнал.
Коэффициент 
- Знаменатель преобразованной передаточной функции позволяет построить обратные линии связи (аналогично). Коэффициенты знаменателя со знаком (+) соответствуют отрицательным обратным связям и наоборот. Наличие единицы в знаменателе обязательно, но оно не отображается на СПС.
В методе пространства состояния (если нет иных оговорок) нумерация внутренних переменных идет с конца. Пример: Рассмотрим следующую передаточную функцию: 
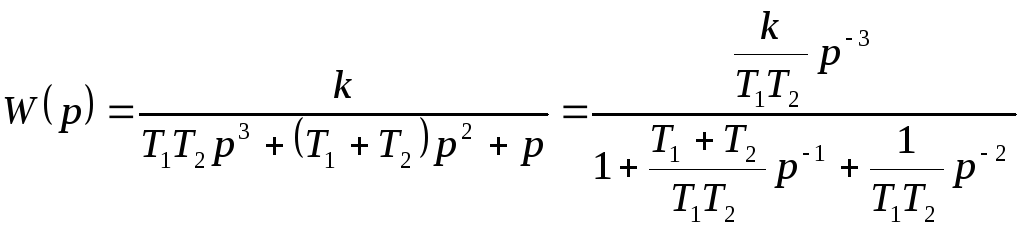








Методы последовательного и параллельного программирования
В этом случае исходная структурная схема представлена в виде соединений звеньев, либо передаточная функция представлена произведением (или суммой) передаточных функций простейших звеньев. В этом случае схема переменных состояния получается путем последовательного построения СПС для каждого из звеньев (базовым методом). Пример: 


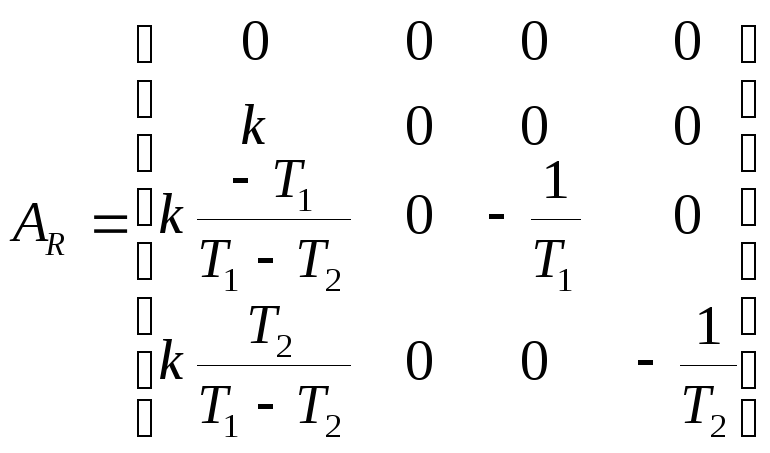

Схемы переменных состояния типовых звеньев
- Апериодическоезвено:

- Колебательноезвено:

- Идеальное интегрирующеезвено:
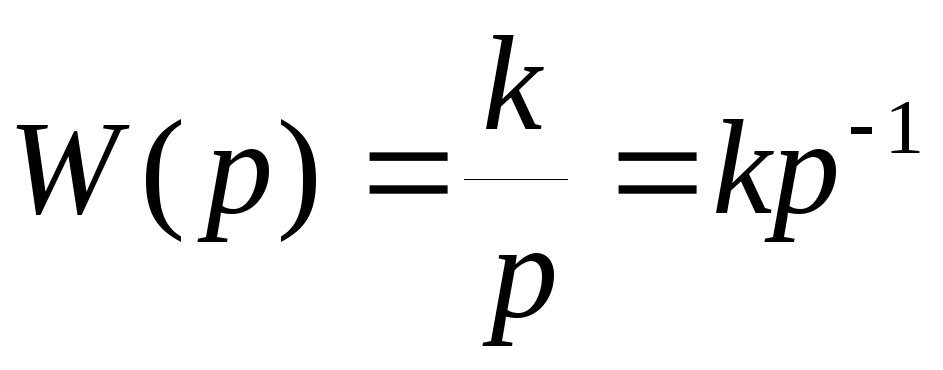
- Идеальное дифференцирующеезвено:

- Реальное дифференцирующеезвено:

- Изодромноезвено:



6.2. Способы построения схем переменных состояния
X (1) (t)=

таких, что каждая из них описывает состояние полностью, причем любые два вектора X (i) (t) и X (j) (t) из этого множества будут однозначно связаны между собой. Удачный выбор переменных состояния часто приводит к существенному упрощению математического описания САУ.
Естественным является стремление выбрать в качестве составляющих вектора состояния контролируемые выходные сигналы системы, характеризующие качество процесса управления, но их обычно бывает недостаточно для полного математического описания САУ. Выбор вектора переменных состояния осуществляется одним из следующих трех способов, называемых методами программирования:
Метод прямого программирования
Пусть передаточная функция системы имеет вид: 
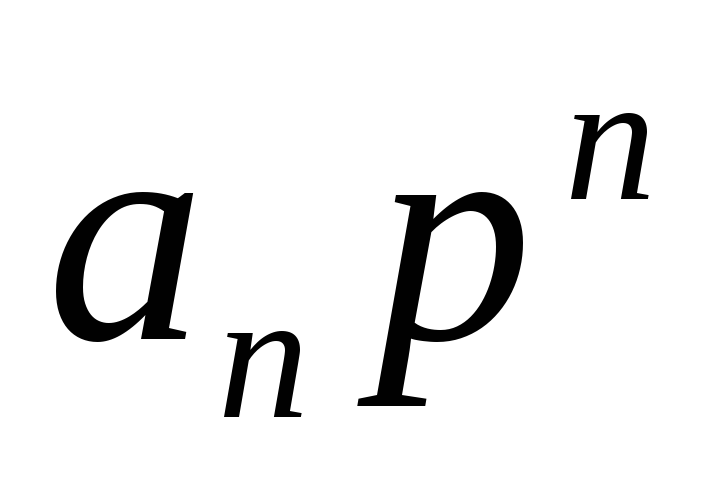














Метод параллельного программирования
Для построения схем переменных состояния способом параллельного программирования передаточная функция системы (6.9), имеющая в общем случае 



Метод последовательного программирования
Для построения схем переменных состояния способом последовательного программирования передаточная функция (6.9) в зависимости от числа и вида ее нулей и полюсов должна быть представлена в виде последовательного соединения элементарных звеньев с передаточными функциями вида: 

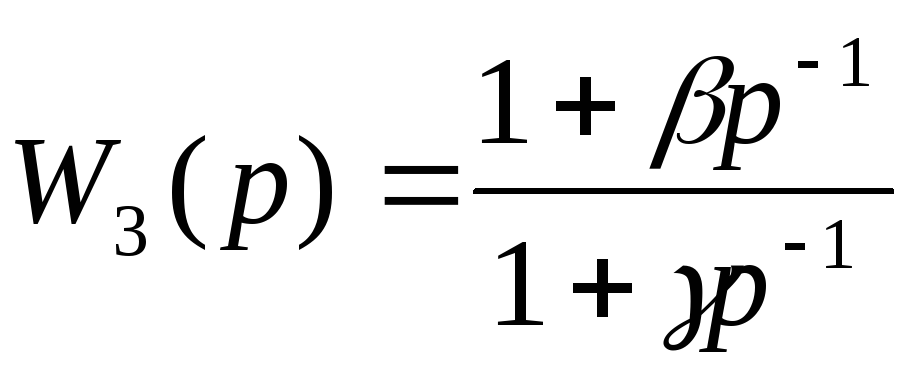






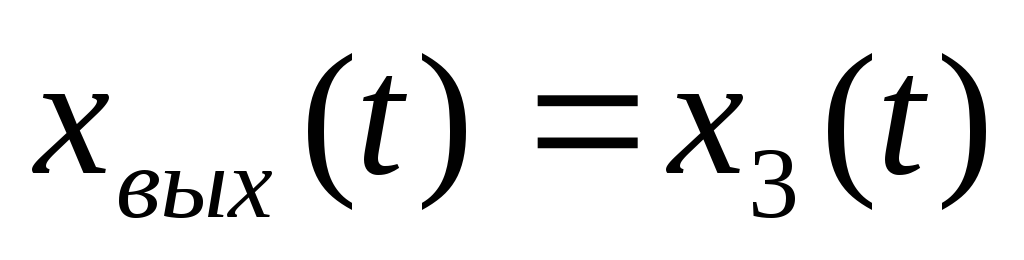

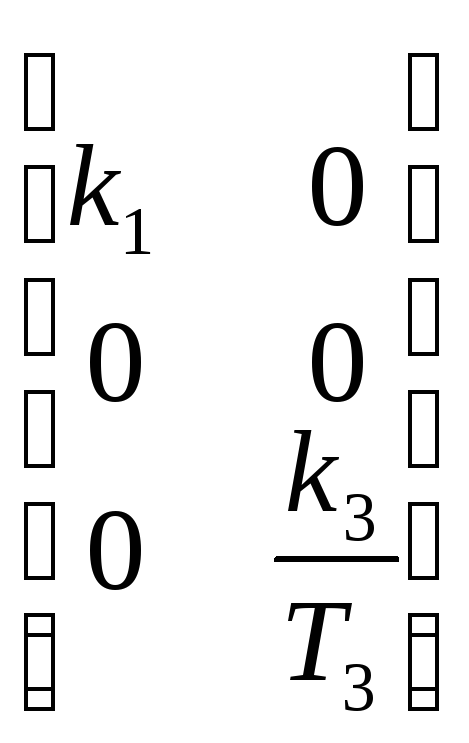






Описание сау методом пространства состояния
Состоянием САУ называется та минимальная информация об объекте, которая позволяет спрогнозировать поведение системы в будущем при известных задающих воздействиях.
С точки зрения ТАУ, объект представляет собой черный ящик, характеризующийся рядом координат.
остояние объекта в любой момент времени определяется тремя векторными пространствами:
- Векторное пространство входа
определяет входные воздействия на объект.
- Векторное пространство внутреннего состояния
определяет реакцию системы на входное воздействие.
- Векторное пространство выхода
определяется выходными переменными.
Совокупность этих векторов определяет состояние системы (пространства состояния). Для непрерывных линейных систем динамика и статика объекта описываются следующими уравнениями: 
- Первое уравнение описывает динамику САУ;
- Второе уравнение описывает статику САУ.
На практике бывает удобней объединить вектор входа и внутреннего состояния в один: 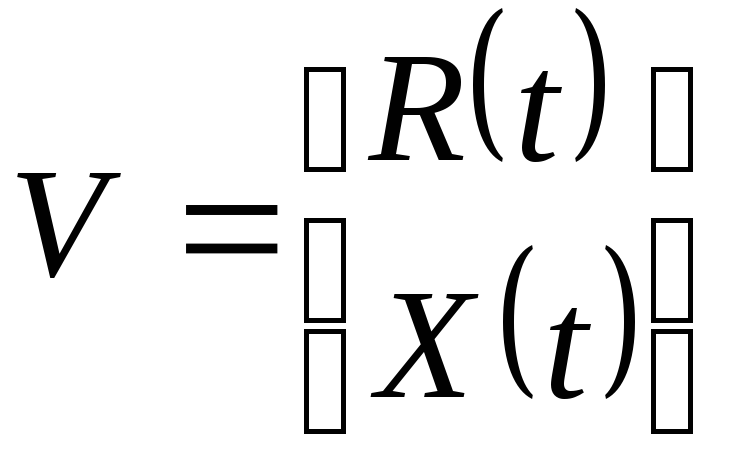


Схемы переменных состояний (спс)
В основе СПС лежит единичный интегратор: С хемы переменных состояния строятся по передаточной функции объекта. Существует три способа построения схем состояния:
- метод прямого программирования;
- метод параллельного программирования;
- метод последовательного программирования.
Метод прямого программирования
Используется, если описание САУ представлено в виде передаточной функции: 


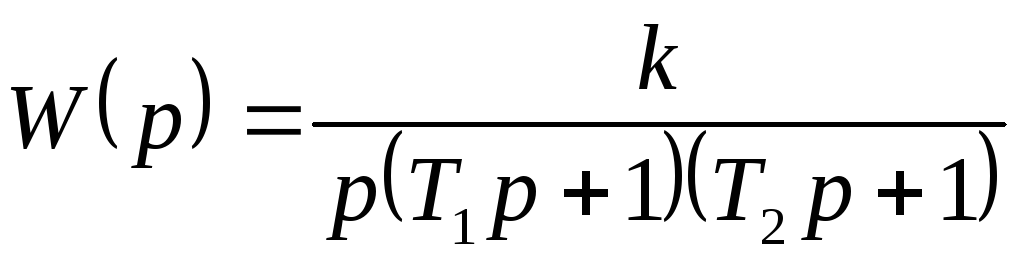


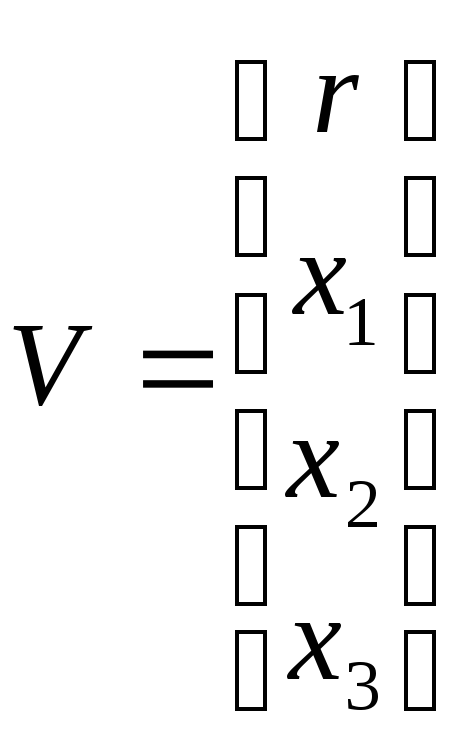





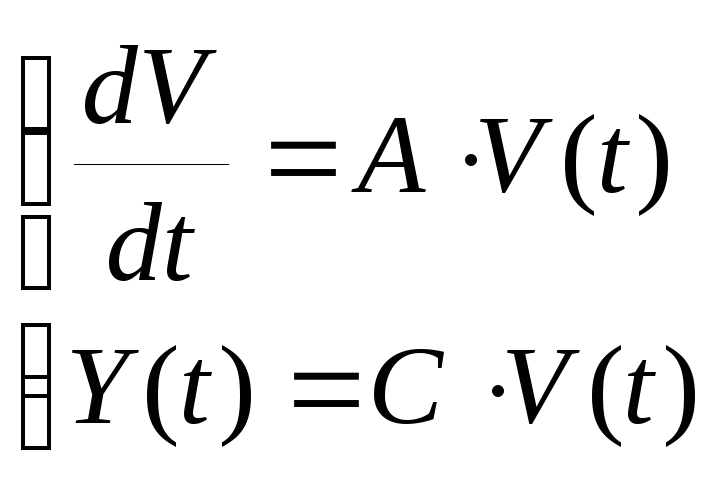
Метод параллельного программирования
Передаточная функция предварительно разбивается на сумму следующих дробей: 




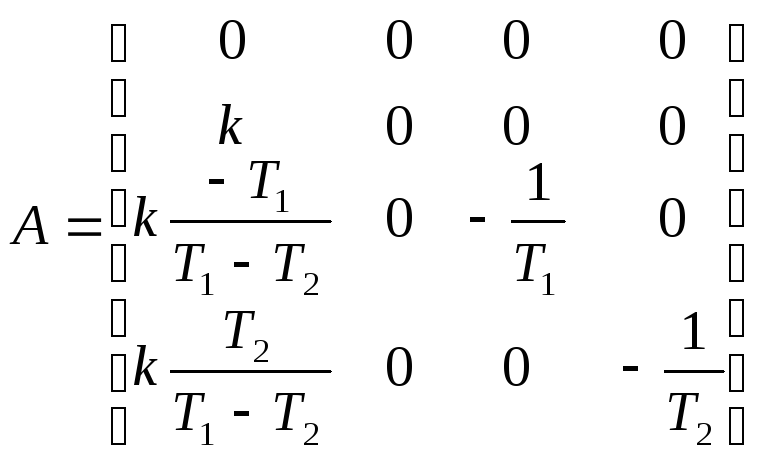





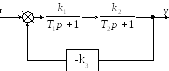





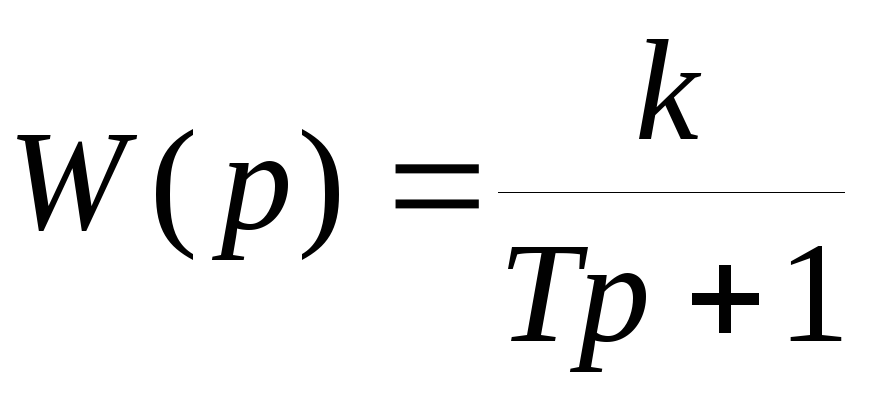





 в наивысшей степени, (переходя тем самым к отрицательным степеням
в наивысшей степени, (переходя тем самым к отрицательным степеням ), а также на коэффициентa0. СПС построить невозможно, если m > n.
), а также на коэффициентa0. СПС построить невозможно, если m > n.

 того) интегратора умножается на соответствующий коэффициент (
того) интегратора умножается на соответствующий коэффициент ( ), затем получившиеся сигналы суммируются. Если коэффициент (
), затем получившиеся сигналы суммируются. Если коэффициент ( ) = 0, то это говорит об отсутствии соответствующего сигнала. Количество слагаемых числителя преобразованной передаточной функции равно количеству сигналов, образующих выходной сигнал.
) = 0, то это говорит об отсутствии соответствующего сигнала. Количество слагаемых числителя преобразованной передаточной функции равно количеству сигналов, образующих выходной сигнал.


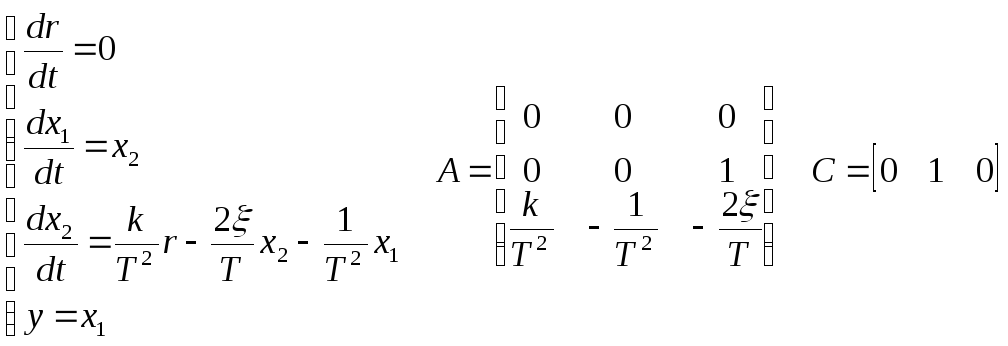
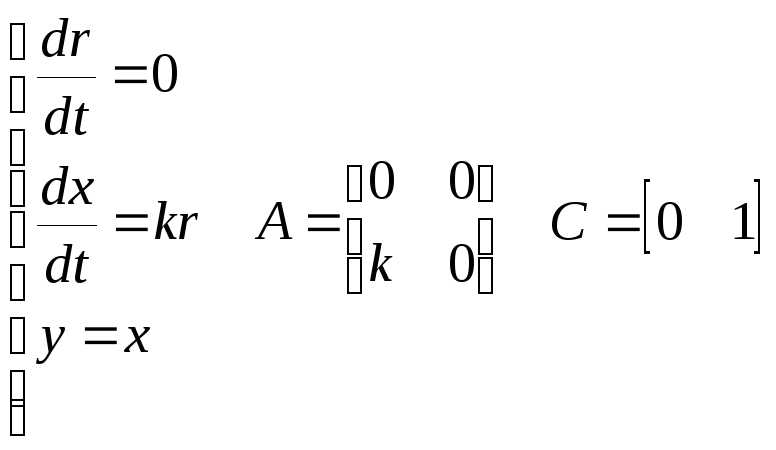












 определяет входные воздействия на объект.
определяет входные воздействия на объект. определяет реакцию системы на входное воздействие.
определяет реакцию системы на входное воздействие. определяется выходными переменными.
определяется выходными переменными.