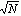Глава V. Нелинейное программирование
Методы нелинейного программирования – это численные методы отыскания минимума (максимума) функций многих переменных при наличии ограничений типа равенств и неравенств, имеющих нелинейный вид, т.е. требуется найти такой вектор , при котором функция
достигает минимума, при выполнении ограничений
Метод линеаризации. Суть метода линеаризации заключается в следующем. Выполняется линеаризация всех соотношений (5.1) – (5.3). Для этого применяется разложение в ряд Тейлора с удержанием только линейных составляющих. Разложение выполняется в окрестности точки , которой следует задаться. Итак, вместо (5.1) – (5.3) имеем для k-той итерации:
Соотношения (5.4) позволяют решать задачу линейного программирования.
Таким образом, может быть построена последовательность точек , которая, вообще говоря, может привести к точке , являющийся решением задачи (5.1) – (5.3).
Пример. Минимизировать
Пусть . Линеаризованные соотношения
определяют задачу линейного программирования. Решив эту задачу, найдем точку первого приближения , затем находится точка и т.д.
Рассмотрим геометрическую интерпретацию задачи этого примера. На рис. 5.1 приведены графики, соответствующие ограничениям (5.6) и (5.8), (5.9).
З адача (5.5), (5.6) предполагает нахождение на дуге АВ такой точки, в которой целевая функция (5.5) достигает минимума. Решение этой задачи известно, это точка A.
В результате линеаризации геометрическая интерпретация задачи изменилась. Теперь среди точек прямой требуется найти такую точку, в которой функция (5.7) достигает минимума. Как было сказано выше, это задача определяется соотношениями (5.7) – (5.9). Оправдано, однако, добавление к этим соотношениям дополнительных неравенств, которые бы ограничивали область поиска решения. Эти дополнительные ограничения вводятся из следующих соображений. Ошибка линеаризации по мере удаления от точки все больше и больше возрастает, см., например, зависимости и . В таких условиях вполне оправдано введение ограничений
г де и некоторые положительные числа. Полученная при этом новая допустимая область показана на рис. 5.1 и 5.2.
Таким образом, уже среди точек отрезка должна быть найдена точка, в которой целевая функция (5.7) достигает минимума.
Совершенно аналогично следует поступать при любой итерации, причем, числа и от итерации к итерации следует постепенно уменьшать.
Алгоритм нелинейного программирования
Излагаемый ниже алгоритм позволяет решать задачу нелинейного программирования в постановке (5.1) – (5.3).
В качестве начальной точки может быть выбрана любая точка, т.е. как точка, принадлежащая допустимой области D (определяется ограничениями (5.2), (5.3)), так и точки, не принадлежащие ей. Если , то в первую очередь организуется наискорейший спуск «почти в область D», а затем включается в работу метод линеаризации. Если , то сразу применяется метод линеаризации.
Рассмотрим, что входит в понятие «почти в область D» и как организуется наискорейший спуск в эту область. «Почти областью D» называется вся совокупность точек x, для которых имеют место ограничения
где , – некоторые малые положительные числа. Эти числа должны быть такими, что выполнение условий (5.10) может расцениваться как практически удовлетворительное выполнение равенств
(строго говоря, точного выполнения этих равенств практически добиться не возможно вообще). Таким образом, «почти область D» определяется ограничениями (5.10), (5.11).
Наискорейший спуск почти в область D осуществляется в результате минимизации функции
Как только обратится в ноль, решается задача линейного программирования, затем вновь проверяются все ограничения и т.д. Задача (5.5), (5.6) по этому методу решается примерно так, как это показано на рис. 5.3.
Н а этом рисунке , ; , – траектории спуска «почти в область D», , ; , – траектории, соответствующие методу линеаризации.
Тема 3 Нелинейное программирование
Одновременно с развитием линейного программирования большое внимание уделялось задачам нелинейного программирования, в которых либо целевая функция, либо ограничения, либо то и другое нелинейны. В 1951 г была опубликована работа Куна и Таккера, в которой приведены необходимые и достаточные условия оптимальности для решения задач нелинейного программирования. Эта работа послужила основой для последующих исследований в этой области.
Начиная с 1955 г опубликовано много работ, посвященных квадратическому программированию (работы Била, Э. Баранкина (Barankin E.) и Дорфмана (Dorfman R.), Франка (Frank M.) и Вольфа (Wolfe P.), Г. Марковица и др.). В работах Денниса (Dennis J. B.), Розена (Rosen J. B.) и Зонтендейка (Zontendijk G.) разработаны градиентные методы решения задач нелинейного программирования.
В настоящее время для эффективного применения методов математического программирования и решения задач на компьютерах разработаны алгебраические языки моделирования, представителями которыми являются AMPL и LINGO.
Многообразие методов решения линейных программ имеет в своей основе идею упорядоченного перебора опорных планов (вершин) исходной или сопряженной задачи. Для нелинейных же программ простого метода решения, подобного cимплексному, нет по многим причинам.
Во-первых, множество планов может оказаться невыпуклым или иметь бесконечное количество «вершин».
Во-вторых, искомые экстремумы могут достигаться как на границе множества планов, так и внутри его.
В-третьих, в нелинейных программах возникает проблема поиска глобального экстремума среди множества локальных.
Как мы показали ранее, ни использование аппарата производных, ни прямое табулирование целевой функции над множеством планов не решают проблему в случае более трех переменных. Поэтому каждая нелинейная программа требует индивидуального подхода, учитывающего ее специфику.
Существующие методы нелинейного программирования можно подразделить на следующие основные классы.
Градиентные методы, в основе которых лежит свойство градиента функции в точке (вектора частных производных, вычисленного в точке) как указателя направления наибольшего роста функции в окрестности точки.
Так при отсутствии ограничений одна из простейших разновидностей градиентных методов — метод наискорейшего спуска предлагает выбрать некоторую точку (план) Xk и начальный шаг Hk, вычислить градиент функции в выбранной точке grad F(Xk) и осуществить переход по градиенту (при максимизации) с выбранным шагом. Если значение функции в новой точке больше предыдущего, новая точка принимается за исходную и повторяется такая же процедура. При попадании в точку с меньшим значением уменьшается шаг (например, вдвое) и переход повторяется от исходной точки. Переходы продолжаются до достаточно малого шага.
Например, если нужно решить систему уравнений
то можно заменить эту задачу задачей минимизации функции F(X,Y)=[(X 2 +1)(Y-2)-3]2+[Y-ln(X+1)] 2 (если система имеет решение, то искомый минимум равен нулю).
Градиент этой функции определяется вектором
Выбираем начальную точку M0(2,1) и шаг h=1.Здесь значение функции F(M0)=64, градиент в этой точке grad F(M0) =[64.066, -80.197], нормированный градиент (вектор единичной длины, составленный из компонент, деленных на корень из суммы их квадратов) gradн F(M0) = [0.62, -0.78]. Смещаемся в направлении, обратном градиенту (ищем минимум), с выбранным шагом в точку М1=М0-h gradн F(M0)=(2-1 0.62, 1+1 0.78)=(1.38, 1.78) и обнаруживаем, что F(M1)=14 < F(M0).
Аналогичный переход с учетом gradн F(M1) = [0.19, -0.98] приводит в точку М2(1.19, 2.76), где F(M2)=5.26, gradн F(M2) = [-0.96, -0.27]. Переход в очередную точку М3(2.15, 3.03) дает F(M3)=11.33 > F(M2).Соответственно уменьшаем шаг вдвое (h=0.5) и получаем точку М4(2.15, 3.03), где F(M4)=3.78, gradн F(M2) = [0.12, 0.99]. Очередной переход приводит в точку с большим значением функции и приходится еще уменьшать шаг и т.д.
Есть и более эффективные переходы по градиенту, связанные с выбором различного шага по разным координатам или с автоматическим определением шага (при каждом переходе решается задача поиска экстремума функции в заданном направлении). Однако, гарантии нахождения глобального экстремума нет (при разных начальных точках или шагах можно получить разные решения для многоэкстремальных функций).
Градиентные методы для задач с ограничениями, где при смещениях по градиенту приходится сталкиваться с опасностью «выскочить» за пределы допустимого множества решений, существенно усложняются (модифицированный метод Ньютона, методы возможных направлений Зойтендейка, сопряженных градиентов, проектируемых градиентов Розена и др.).
Существует обширная литература по численному анализу, где значительное внимание уделяется градиентным и другим итерационным методам, но тем не менее решение нелинейных задач оптимизации при наличии ограничений иногда весьма затруднительно.
Методы Монте-Карло. Здесь отыскивается n — мерный параллелепипед, включающий в себя множество планов, и затем моделируются N случайных точек с равномерным законом распределения в параллелепипеде (практически во всех программных средах предусмотрено наличие соответствующих датчиков псевдослучайных чисел).
В точках, попавших во множество планов, вычисляются значения функции и запоминается точка текущего экстремума. После этого берется параллелепипед меньших размеров с центром в найденной точке, и в нем вновь моделируются N случайных точек. Процесс такого стохастического моделирования заканчивается при малых размерах параллелепипеда. Методы Монте-Карло имеют преимущество над моделированием на детерминированной сетке, так как их точность имеет порядок 1/ и не зависит от размерности задачи. Естественно, этими методами никто не пользуется при ручном счете; они просты для программной реализации и обычно используются при поиске начального приближения для градиентных методов.
Методы динамического программирования, сводящие многомерную задачу оптимизации к последовательности задач меньшей размерности.
Методы выпуклого программирования, реализующие поиск минимума выпуклой функции или максимума вогнутой на выпуклом множестве планов. Если множество планов — выпуклый многогранник, то эти методы допускают использование симплексного метода.
Наиболее эффективно эти и другие методы решения действуют для так называемых сепарабельных функций, т.е. функций, представимых в виде суммы функций одной переменной