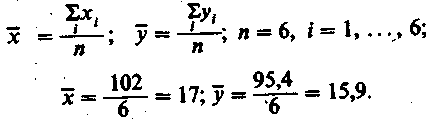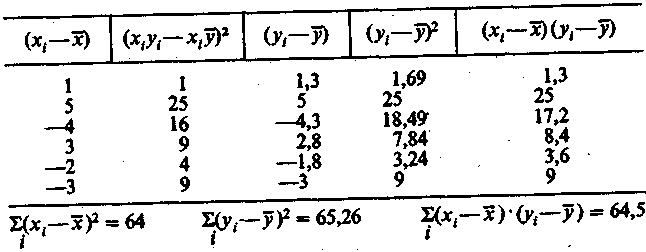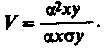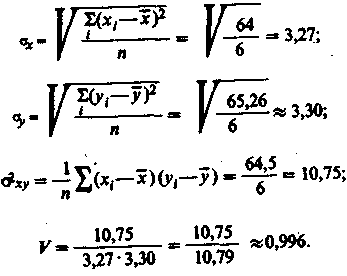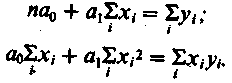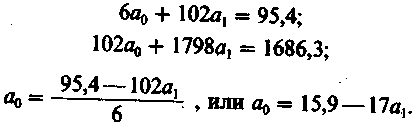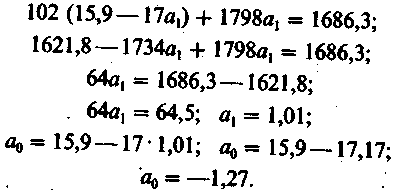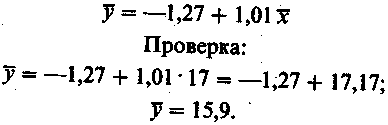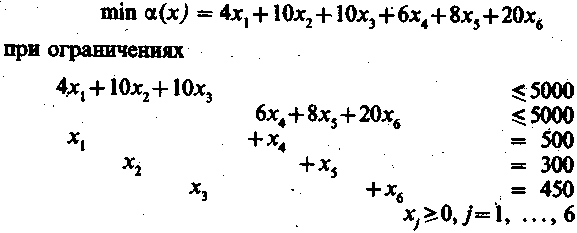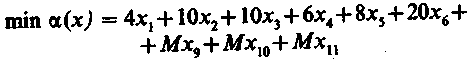Метод линейного программирования метод корреляционного анализа

Метод корреляционно-регрессионного анализа

Метод корреляционного и регрессионного анализа широко используется для определения тесноты связи между показателями, не находящимися в функциональной зависимости. Теснота связи между изучаемыми явлениями измеряется корреляционным отношением (для криволинейной зависимости). Для прямолинейной зависимости исчисляется коэффициент корреляции.

Стохастические зависимости отличаются приблизительностью, неопределенностью. Они проявляются только в среднем по значительному количеству объектов (наблюдений). Здесь каждой величине факторного показателя (аргумента) может соответствовать несколько значений результативного показателя (функций).

Корреляционная (стохастическая) связь – это неполная, вероятностная зависимость между показателями, которые проявляются только в массе наблюдений.

Парная корреляция – связь между двумя показателями, один из которых является факторным, а другой – результативным. Множественная корреляция возникает от взаимодействия нескольких факторов с результативным показателем.

Необходимые условия применения корреляционного анализа:

1) наличие достаточно большого количества наблюдений о величине исследуемых факторных и результативных показателях (в динамике или за текущий год по совокупности однородных объектов);

2) исследуемые факторы должны иметь количественное измерение и отражение в тех или иных источниках информации.

Применение корреляционного анализа позволяет решить следующие задачи:

1) определить изменения результативного показателя под воздействием одного или нескольких факторов (в абсолютном измерении). Это значит, определить, на сколько единиц изменится величина результативного показателя при изменении факторного на единицу;

2) установить относительную степень зависимости результативного показателя от каждого фактора.

Значительно углубляется факторный анализ, устанавливается место и роль каждого фактора в формировании уровня исследуемых показателей, углубляется знание об изучаемых явлениях, определяется закономерности их развития и как итог – точнее обосновываются планы и управленческие решения, более объективно оцениваются итоги деятельности предприятия и более полно внутрихозяйственные резервы.

Методы линейного программирования

Методы линейного программирования применяются для решения многих экстремальных задач, с которыми довольно часто приходится иметь дело в экономике. Решение таких задач сводится к нахождению крайних значений (максимума и минимума) некоторых функций переменных величин.

Линейное программирование основано на решении системы линейных уравнений (с преобразованием в уравнения и неравенства), когда зависимость между изучаемыми явлениями строго функциональна. Для него характерны математическое выражение переменных величин, определенный порядок, последовательность расчетов (алгоритм), логический анализ. Применять его можно только в тех случаях, когда изучаемые переменные величины и факторы имеют математическую определенность и количественную ограниченность, когда в результате известной последовательности расчетов происходит взаимозаменяемость факторов, когда логика в расчетах, математическая логика совмещаются с логически обоснованным пониманием сущности изучаемого явления.

С помощью этого метода в промышленном производстве, например, исчисляется оптимальная общая производительность машин, агрегатов, поточных линий (при заданном ассортименте продукции и иных заданных величинах), решается задача рационального раскроя материалов (с оптимальным выходом заготовок). В сельском хозяйстве он используется для определения минимальной стоимости кормовых рационов при заданном количестве кормов (по видам и содержащимся в них питательным веществам). Задача о смесях может найти применение и в литейном производстве (состав металлургической шихты). Этим же методом решаются транспортная задача, задача рационального прикрепления предприятий – потребителей к предприятиям – производителям.

Все экономические задачи, решаемые с применением линейного программирования, отличаются альтернативностью решения и определенными ограничивающими условиями. Решить такую задачу – значит выбрать из всех допустимо возможных (альтернативных) вариантов лучший, оптимальный. Важность и ценность использования в экономике метода линейного программирования состоят в том, что оптимальный вариант выбирается из весьма значительного количества альтернативных вариантов. При помощи других способов решать такие задачи практически невозможно.

Источник

8.2. Метод корреляционно-регрессионного анализа

Метод корреляционного и регрессионного анализа широко используется для определения тесноты связи между показа­телями, не находящимися в функциональной зависимости. Тес­нота связи между изучаемыми явлениями измеряется корреля­ционным отношением (для криволинейной зависимости). Для прямолинейной зависимости исчисляется коэффициент корре­ляции.

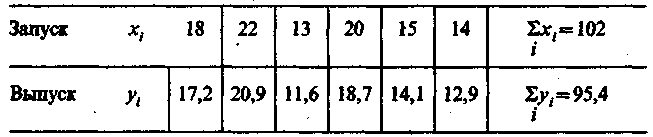
Одной из распространенных аналитических задач, реша­емых с применением корреляционно-регрессионного метода, является задача на запуск — выпуск. Допустим, что имеются фактические данные о запуске и выпуске промышленных изде­лий (табл. 3).

Требуется определить зависимость выпуска изделий в сре­днем от их запуска, составив соответствующее уравнение ре­грессии.

Значения x и у определяются по формулам:

Дальнейшим вычислениям придается табличная форма, что повышает их наглядность (табл. 4).

Теснота связи между показателями запуска и выпуска изме­ряется коэффициентом корреляции, который исчисляется по формуле:

Подставляя соответствующие значения, получим:

Считая формулу связи линейной (у = a0 + а1х), определим зависимость выпуска промышленных изделий от их запуска. Для этого решается система нормальных уравнений:

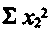
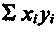
Величины и представлены в следующей таблице (табл. 5.)

Значение a0 определяем из первого уравнения:

Подставляя найденное выражение а0 во второе уравнение, находим значение а1:

Итак, уравнение регрессии в окончательном виде получило следующий вид:

8.3. Методы линейного программирования

Методы линейного программирования применяются для решения многих экстремальных задач, с которыми до­вольно часто приходится иметь дело в экономике. Решение таких задач сводится к нахождению крайних значений (ма­ксимума и минимума) некоторых функций переменных ве­личин.

Линейное программирование основано на решении систе­мы линейных уравнений (с преобразованием в уравнения и не­равенства), когда зависимость между изучаемыми явлениями строго функциональна. Для него характерны математическое выражение переменных величин, определенный порядок, по­следовательность расчетов (алгоритм), логический анализ. Применять его можно только в тех случаях, когда изучаемые переменные величины и фактору имеют математическую определенность и количественную ограниченность, когда в ре­зультате известной последовательности расчетов происходит взаимозаменяемость факторов, когда логика в расчетах, мате­матическая логика совмещаются с логически обоснованным пониманием сущности изучаемого явления.

С помощью этого метода в промышленном производстве, например, исчисляется оптимальная общая производитель­ность машин, агрегатов, поточных линий (при заданном ассор­тименте продукции и иных заданных величинах), решается задача рационального раскроя материалов (с оптимальным выходом заготовок). В сельском хозяйстве он используется для определения минимальной стоимости кормовых рационов при заданном количестве кормов (по видам и содержащимся в них питательным веществам). Задача о смесях может найти применение и в литейном производстве (состав металлургичес­кой шихты). Этим же методом решаются транспортная зада­ча, задача рационального прикрепления предприятий-потреби­телей к предприятиям-производителям.

Все экономические задачи, решаемые с применением линей­ного программирования, отличаются альтернативностью ре­шения и определенными ограничивающими условиями. Ре­шить такую задачу — значит выбрать из всех допустимо возможных (альтернативных) вариантов лучший, оптималь­ный. Важность и ценность использования в экономике метода линейного программирования состоят в том, что оптималь­ный вариант выбирается из весьма значительного количества альтернативных вариантов. При помощи других способов ре­шать такие задачи практически невозможно.

В качестве примера рассмотрим решение задачи рациона­льности использования времени работы производственного оборудования.

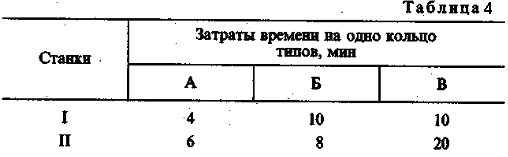
В соответствии с оперативным планом участок шлифовки за первую неделю декабря выпустил 500 колец для подшип­ников типа А, 300 колец для подшипников типа Б и 450 колец для подшипников типа В. Все кольца шлифовались на двух взаимозаменяемых станках разной производительности. Ма­шинное время каждого станка составляет 5000 мин. Трудоем­кость операций (в минутах на одно кольцо) при изготовлении различных колец характеризуется следующими данными (табл. 4).

Следует определить оптимальный вариант распределения операций по станкам и время, которое было бы затрачено при этом оптимальном варианте. Задачу выполним симплексным методом.

Для составления математической модели данной задачи введем следующие условные обозначения:

х_1, х_г, х₃, — соответственно количество колец для подшип­ников типов А, Б, В, производимых на станке I;

х_4, х_5, х_6, — соответственно количество колец для подшип­ников типов А, Б, В, производимых на станке II.

Линейная форма, отражающая критерий оптимальности, будет иметь вид:

Преобразуем условие задачи введением дополнительных (вспомогательных) и фиктивных переменных. Условие запи­шем так:

Система уравнений, отражающая ограничительные усло­вия машинного времени и количество произведенной про­дукции:

Решение этой задачи представлено в табл. 6.6. Оптимальный вариант получен на седьмом этапе (итерации). Если бы на станке I производилось 125 колец подшипников типа А, 450 колец подшипников типа В, на станке II — 375 колец подшипников типа А и 300 колец подшипников типа Б, то при такой загрузке оборудования было бы высво­бождено 350 мин машинного времени станка П. Общие затраты времени по оптимальному варианту составили бы 9650 мин, тогда как фактически затрачено 10000 мин ма­шинного времени.

Весьма типичной задачей, решаемой с помощью линейного программирования, является транспортная задача. Ее смысл заключается в минимизации грузооборота при доставке товаров широкого потребления от производителя к потребителю, с оптовых складов и баз в розничные торговые предприятия. Она решается симплекс-методом или распределительным методом.

Источник