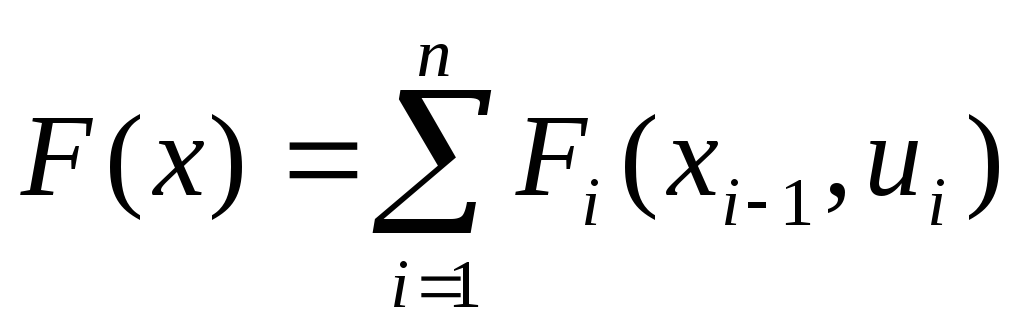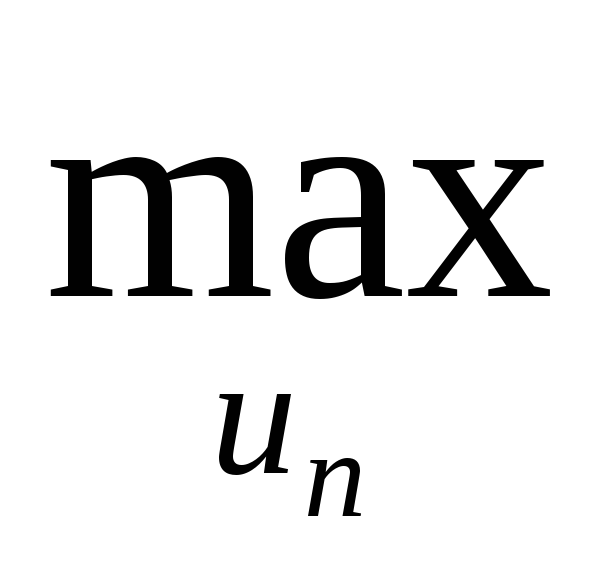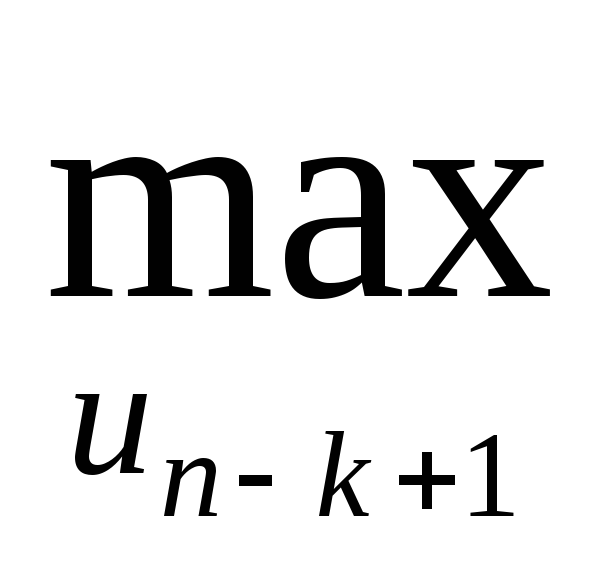§1. Динамическое программирование как метод оптимизации.
Динамическое программирование (ДП) – это метод оптимизации многошаговых процессов принятия решений, позволяющий указать пути исследования целого класса экстремальных задач. Этот метод оказывается эффективным для задач с сепарабельной целевой функцией (функция нескольких переменных, которая представляет собой сумму функций одной переменной). К таким задачам, в частности, относятся задачи линейного программирования.
Многие экономические задачи расчленяются на шаги естественным образом. К ним относятся задачи планирования и управления, в которых естественным шагом является год, квартал, месяц, неделя, день и т.д. Кроме этого метод ДП может использоваться при решении задач, в которых время вообще не фигурирует. Необходимость принятия решений возникает тогда, когда производятся те или иные целенаправленные действия; например, некоторая физическая система переводится из одного состояния в другое посредством приложения управляющих воздействий. Если подобные ситуации повторяются периодически, то организуется процесс принятия решений. К таким задачам относятся задачи оптимального управления.
Итак, рассмотрим некоторый многошаговый процесс. Его нужно организовать так, чтобы получить наилучший результат с точки зрения принятого критерия Z оптимальности. Если этот критерий имеет числовое значение, то критерий оптимальности нужно минимизировать или максимизировать.
Пусть процесс принятия решения разбивается на n шагов. Действия, совершаемые на j-ом шаге, характеризуются совокупностью показателей . Состояние процесса к началу этого шага характеризуется совокупностью параметров = . Очевидно, что вектор управления является функцией состояния системы: = (). Начальное состояние системы задано. Результирующее значение критерия Z определяется теми , j =1, которые были приняты ранее: Z=Z(, , …, ).
Возникает вопрос: как выбрать , , …, , чтобы величина Z приняла экстремальное значение? Можно рассматривать Z как функцию переменных , используя для нахождения экстремума один из известных способов оптимизации. Однако этот путь не всегда прост. Появилась идея провести оптимизацию поэтапно, анализируя последовательно каждый шаг процесса в поисках варианта его наилучшего продолжения. Эта идея лежит в основе метода динамического программирования.
Итак, важным условием применимости метода динамического программирования является возможность разбиения процесса принятия решений на ряд однотипных шагов, каждый из которых планируется отдельно, но с учетом результатов, полученных на предыдущих шагах.
Динамическое программирование основывается на двух важных принципах: принцип оптимальности и принцип вложения (или погружения).
Принцип оптимальности: необходимо всегда обеспечивать оптимальное (в смысле принятого критерия) продолжение процесса относительно уже достигнутого состояния. Другими словами, на каждом шаге решение должно приниматься оптимальное и должно учитывать результат, полученный на предыдущих шагах. С точки зрения математики это реализуется в составлении неких рекуррентных соотношений.
Принцип вложения (погружения). Природа задачи, для которой используется метод ДП, не меняется при изменении числа шагов, поэтому задача погружается в семейство подобных задач, являясь одной из них.
Реализация названных принципов дает гарантию, что 1) решение, принимаемое на очередном шаге, окажется лучшим с точки зрения всего процесса; 2) последовательность решений одношаговой, двухшаговой и т.д. задач приведет к решению исходной n-шаговой задачи.
Схема динамического программирования чаще всего (но не всегда) строится так, что первым исследуется последний (конечный) шаг задачи. Этот завершающий этап может быть спланирован наилучшим образом с точки зрения критерия Z сам по себе. Но (!) с учетом ожидаемых исходов предыдущего этапа, еще не исследованного. Поэтому получаем набор условно оптимальных решений.
Завершив исследование последнего этапа, применяют те же рассуждения для предпоследнего этапа, но теперь цель – достигнуть экстремального значения Z не на одном (предпоследнем) этапе, а на двух последних вместе. Тем самым будет найден второй набор условно оптимальных решений. Повторяем подобные операции для третьего, четвертого и т.д. этапов, в результате получаем решение задачи.
Отметим преимущества метода динамического программирования:
- Дает возможность решать задачи, которые ранее не исследовались из-за отсутствия математического аппарата, например, конечномерные задачи с дискретной структурой.
- Позволяет упростить поиск оптимальных решений в ряде случаев за счет резкого сокращения объемов вычислений, например, в комбинаторных задачах.
Отметим недостатки метода динамического программирования:
- Отсутствие универсального алгоритма, пригодного для решения всех задач (есть общая идея, а алгоритм формируется для каждой конкретной задачи отдельно). Поэтому результат во многом зависит от опыта математика-исследователя.
- Трудности при анализе задач большой размерности (для решения конкретных задач нужны ЭВМ с большой оперативной памятью, поскольку размер таблиц от этапа к этапу может расти экспоненциально). Этот недостаток даже получил специальное название – «проклятие размерности».
Лекция 7,8. Метод динамического программирования.
Вопросы: 1. Основные понятия. Общая постановка задачи ДП.
2. Принцип оптимальности. Функциональные уравнения Беллмана.
3. Задача оптимального распределения ресурсов.
5. Задача управления производством и запасами.
1.Основные понятия. Общая постановка задачи динамического программирования.
Динамическое программирование — метод оптимизации, приспособленный к операциям, в которых процесс принятия решений может быть разбит на отдельные этапы, шаги.
Такие операции называются многошаговыми. Многие экономические процессы расчленяются на шаги естественным образом. Это процессы планирования и управления, развиваемые во времени. Естественным шагом может быть год, квартал, месяц и т.д. Т.о., если управление сводится к однократному принятию решения, то соответствующая задача называется одноэтапной или одношаговой. Ранее решаемые задачи линейного и нелинейного программирования – примеры подобных задач.Если управление требует некоторой последовательности принятых решений, то такая задача называется многоэтапной или многошаговой.
Рассмотрим некоторую управляемую систему, характеризующуюся определенным набором параметров, задающих ее состояния. Система под влиянием управления переходит из начального состояния в конечное. Введем обозначения.
1. xi–многомерный вектор, компоненты которого определяют состояние системы на
i-том шаге. Дальнейшее изменение состояния зависит только от данного состояния и не
зависит от того, каким путем система перешла в него (процесс без последствия).
2.На каждом шаге выбирается одно решение,управление ui, под действием которого
система переходит из предыдущего состояния xi-1 в новое xi. Это новое состояние
является функцией состояния на начало шага xi-1и принятого в начале решенияui, т.е.
3. Действие на каждом шаге связано с определенным выигрышем (доходом, прибылью)
или потерей (издержками), которые зависят от состояния на начало шага и принятого
решения. Fi – приращение целевой функции задачи в результате i-того шага,
аналогично, Fi = Fi ( xi-1 , ui ).Тогда значение целевой функции при переходе системы
из начального состояния в конечное за nшагов
.
4.На векторы состояния хiи управленияuiмогут быть наложены ограничения,
объединение которых составляет область допустимых решений uU.
5.Требуется найти такое допустимое управлениеu* = (u1* ,…,un* ) (для каждого шага),
чтобы получить экстремальное значение функции цели F* за всеnшагов.
Любая последовательность действий для каждого шага, переводящая систему из начального состояния в конечное, называется стратегией управления.
Допустимая стратегия управления, доставляющая функции цели экстремальное значение, называется оптимальной.
2. Принцип оптимальности. Функциональные уравнения Беллмана.
Метод динамического программирования состоит в том, что оптимальное управление строится постепенно, шаг за шагом. На каждом шаге оптимизируется управление только этого шага. Вместе с тем на каждом шаге управление выбирается с учетом последствий, т.к. управление, оптимизирующее целевую функцию только для данного шага, может привести к неоптимальному эффекту всего процесса. Управление на каждом шаге должно быть оптимальным с точки зрения процесса в целом. В основе метода динамического программирования лежит принцип оптимальности, сформулированный Беллманом.
Принцип оптимальности: если некоторая последовательность решений оптимальна, то на любом шаге последующие решения образуют оптимальную стратегию по отношению к результату предыдущих решений.
Другими словами, каково бы не было состояние системы перед очередным шагом, надо выбрать управление на этом шаге так, чтобы выигрыш на данном шаге (проигрыш) плюс оптимальный выигрыш (проигрыш) на всех последующих шагах был бы максимальным (минимальным). На основе принципа оптимальности Беллмана строится схема решения монгошаговой задачи, состоящая из 2-х частей:
1) Обратный ход:от последнего шага к первому получают множество возможных оптимальных («условно-оптимальных») управлений.
2) Прямой ход:от известного начального состояния к последнему из полученного множества «условно-оптимальных» управлений составляется искомое оптимальное управление для всего процесса в целом.
Оптимальную стратегию управления можно получить, если сначала найти оптимальную стратегию управления на n-м шаге, затем на двух последних шагах, затем на трех последних шагах и т.д., вплоть до первого шага.
Чтобы можно было использовать принцип оптимальности практически, необходимо записать его математически. Обозначим через z1(xn-1),z2(xn-2),…,zn(x0) условно-оптимальные значения приращений целевой функции на последнем шаге, двух последних,…, на всей последовательности шагов, соответственно.
Тогда для последнего шага:
z1(xn-1) =(min) n(xn-1,un)>,
где un– множество допустимых (возможных) управлений наn-ом шаге,xn-1– возможные состояния системы передn-ым шагом.
Для двух последних шагов:
z2(xn-2) =(min) n-1(xn-2,un-1) +z1(xn-1)>.
Для k последних шагов:
zk(xn-k) = (min) n-k+1(xn-k, un-k+1) + zk-1(xn-k+1)>.
Для всех n шагов:
zn(x0) = (min) 1(x0, u1) + zn-1(x1)>.
Полученные рекуррентные соотношения называют функциональными уравнениями Беллмана.
При этом согласно определению zn(x0) =F*.