Maximum depth of binary tree java

LeetCode 104. Maximum Depth of Binary Tree

The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Note: A leaf is a node with no children.

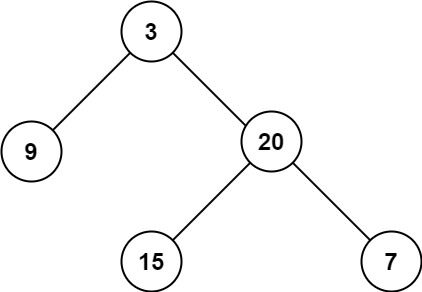
Given binary tree [3,9,20,null,null,15,7] ,

return its depth = 3.Accepted

Explanation

List all scenarios of what a binary tree could be like:

1. when a binary tree is null, simply return maximum depth as 0
2. when a binary tree just have a root node, return maximum depth as 1
3. when a binary tree has a root node and child nodes, maximum depth would be the depth of the bigger side between left and right subtrees plus 1.

Java Solution

/** * Definition for a binary tree node. * public class TreeNode < * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) < val = x; >* > */ class Solution < public int maxDepth(TreeNode root) < if (root == null) < return 0; >int leftDepth = maxDepth(root.left); int rightDepth = maxDepth(root.right); return Math.max(leftDepth, rightDepth) + 1; > >

Python Solution

# Definition for a binary tree node. # class TreeNode: # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution: def maxDepth(self, root: TreeNode) -> int: if root == None: return 0 left = self.maxDepth(root.left) right = self.maxDepth(root.right) max_depth = max(left, right) + 1 return max_depth 

Источник

Question

Given the root of a binary tree, return its maximum depth.

A binary tree’s maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Input: root = [3,9,20,null,null,15,7] Output: 3

Input: root = [1,null,2] Output: 2

Constraints:

Algorithm

BFS

The layer sequence traverses the binary tree, and then counts the total number of layers, which is the maximum depth of the binary tree. Note that the for loop in the while loop has a trick.

You must put q.size() in the initialization, not in the judgment stop In the condition, because the size of q changes at any time, an error will occur in the stop condition.

DFS

Code

import java.util.LinkedList; import java.util.Queue; public class Maximum_Depth_of_Binary_Tree  /** * Definition for a binary tree node. * public class TreeNode < * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) < val = x; >* > */ // bfs public class Solution_countAsMarker  public int maxDepth(TreeNode root)  if (root == null)  return 0; > QueueTreeNode> q = new LinkedList<>(); q.offer(root); int currentLevelCount = 1; int nextLevelCount = 0; int depth = 0; while (!q.isEmpty())  TreeNode current = q.poll(); currentLevelCount--; if (current.left != null)  q.offer(current.left); nextLevelCount++; > if (current.right != null)  q.offer(current.right); nextLevelCount++; > if (currentLevelCount == 0)  currentLevelCount = nextLevelCount; nextLevelCount = 0; depth++; > > return depth; > > // @note: just a bfs, counting total level public class Solution_iteration_nullAsMarker  public int maxDepth(TreeNode root)  if (root == null)  return 0; > QueueTreeNode> q = new LinkedList<>(); q.offer(root); q.offer(null);// @note: use null as marker for end of level int depth = 0; while (!q.isEmpty())  TreeNode current = q.poll(); if (current == null)  depth++; if (!q.isEmpty())  q.offer(null); > continue; > if (current.left != null)  q.offer(current.left); > if (current.right != null)  q.offer(current.right); > > return depth; > > public class Solution_recursion  public int maxDepth(TreeNode root)  if (root == null)  return 0; > if (root.left == null && root.right == null)  return 1; > return 1 + Math.max(maxDepth(root.left), maxDepth(root.right)); > > > ############ /** * Definition for a binary tree node. * public class TreeNode < * int val; * TreeNode left; * TreeNode right; * TreeNode() <>* TreeNode(int val) < this.val = val; >* TreeNode(int val, TreeNode left, TreeNode right) < * this.val = val; * this.left = left; * this.right = right; * >* > */ class Solution  public int maxDepth(TreeNode root)  if (root == null)  return 0; > int l = maxDepth(root.left); int r = maxDepth(root.right); return 1 + Math.max(l, r); > > 

// OJ: https://leetcode.com/problems/maximum-depth-of-binary-tree/ // Time: O(N) // Space: O(N) class Solution  public: int maxDepth(TreeNode* root)  return root ? 1 + max(maxDepth(root->left), maxDepth(root->right)) : 0; > >; 

# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def maxDepth(self, root: TreeNode) -> int: if root is None: return 0 l, r = self.maxDepth(root.left), self.maxDepth(root.right) return 1 + max(l, r) ############ # Definition for a binary tree node. # class TreeNode(object): # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution(object): def maxDepth(self, root): """ :type root: TreeNode :rtype: int """ if not root: return 0 return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1 

/** * Definition for a binary tree node. * type TreeNode struct < * Val int * Left *TreeNode * Right *TreeNode * >*/ func maxDepth(root *TreeNode) int  if root == nil  return 0 > l, r := maxDepth(root.Left), maxDepth(root.Right) return 1 + max(l, r) > func max(a, b int) int  if a > b  return a > return b > 

/** * Definition for a binary tree node. * class TreeNode < * val: number * left: TreeNode | null * right: TreeNode | null * constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) < * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * >* > */ function maxDepth(root: TreeNode | null): number  if (root == null)  return 0; > return 1 + Math.max(maxDepth(root.left), maxDepth(root.right)); > 

/** * Definition for a binary tree node. * function TreeNode(val, left, right) < * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * >*/ /** * @param root * @return */ var maxDepth = function (root)  if (!root) return 0; const l = maxDepth(root.left); const r = maxDepth(root.right); return 1 + Math.max(l, r); >; 

// Definition for a binary tree node. // #[derive(Debug, PartialEq, Eq)] // pub struct TreeNode // pub val: i32, // pub left: Option>>, // pub right: Option>>, // > // // impl TreeNode // #[inline] // pub fn new(val: i32) -> Self // TreeNode // val, // left: None, // right: None // > // > // > use std::rc::Rc; use std::cell::RefCell; impl Solution  fn dfs(root: &OptionRcRefCellTreeNode>>>) -> i32  if root.is_none()  return 0; > let node = root.as_ref().unwrap().borrow(); 1 + Self::dfs(&node.left).max(Self::dfs(&node.right)) > pub fn max_depth(root: OptionRcRefCellTreeNode>>>) -> i32  Self::dfs(&root) > > 

All Problems

All Solutions

Источник

LeetCode – Maximum Depth of Binary Tree (Java)

The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Java Solution

public int maxDepth(TreeNode root) { if(root==null) return 0; int leftDepth = maxDepth(root.left); int rightDepth = maxDepth(root.right); int bigger = Math.max(leftDepth, rightDepth); return bigger+1; }

public int maxDepth(TreeNode root)

Related posts:

If you want someone to read your code, please put the code inside

 and 

tags. For example:

Источник

Maximum Depth of Binary Tree – Leetcode Solution

In this post, we are going to solve the 104. Maximum Depth of Binary Tree problem of Leetcode. This problem 104. Maximum Depth of Binary Tree is a Leetcode easy level problem. Let’s see the code, 104. Maximum Depth of Binary Tree – Leetcode Solution.

Problem

Given the root of a binary tree, return its maximum depth.

A binary tree’s maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Example 1 :

Input: root = [3,9,20,null,null,15,7] Output: 3

Example 2 :

Input: root = [1,null,2] Output: 2

Constraints

Now, let’s see the code of 104. Maximum Depth of Binary Tree – Leetcode Solution.

Maximum Depth of Binary Tree – Leetcode Solution

104. Maximum Depth of Binary Tree – Solution in Java

/** * Definition for a binary tree node. * public class TreeNode < * int val; * TreeNode left; * TreeNode right; * TreeNode() <>* TreeNode(int val) < this.val = val; >* TreeNode(int val, TreeNode left, TreeNode right) < * this.val = val; * this.left = left; * this.right = right; * >* > */ class Solution < public int maxDepth(TreeNode root) < if(root == null) return 0; int leftDepth = maxDepth(root.left); int rightDepth = maxDepth(root.right); return Math.max(leftDepth,rightDepth) + 1; >>

104. Maximum Depth of Binary Tree – Solution in C++

/** * Definition for a binary tree node. * struct TreeNode < * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) <>* TreeNode(int x) : val(x), left(nullptr), right(nullptr) <> * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) <> * >; */ class Solution < public: int maxDepth(TreeNode* root) < if(!root) return 0; int maxLeft = maxDepth(root->left); int maxRight = maxDepth(root->right); return max(maxLeft, maxRight)+1; > >;

104. Maximum Depth of Binary Tree – Solution in Python

# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def maxDepth(self, root: Optional[TreeNode]) -> int: def dfs(root, depth): if not root: return depth return max(dfs(root.left, depth + 1), dfs(root.right, depth + 1)) return dfs(root, 0)

Note: This problem 104. Maximum Depth of Binary Tree is generated by Leetcode but the solution is provided by CodingBroz. This tutorial is only for Educational and Learning purpose.

Источник

Maximum depth of a Binary Tree

Problem Statement: Find the Maximum Depth of Binary Tree. Maximum Depth is the count of nodes of the longest path from the root node to the leaf node.

Input Format: Given the root of Binary Tree

Explanation: Maximum Depth in this tree is 4 if we follow path 5 – 1 – 3 – 8 or 5 – 1 – 3 – 11

Input Format: Given the root of Binary Tree

Explanation: Maximum Depth in this tree is 3 , if we follow path 7 – 1 – 2. If we follow 7 – 3 path then depth is 2 ( not optimal)

Input Format: Given the root of Binary Tree

Explanation: Maximum Depth in this tree is 1 as there is only one node which is the root node.

Note: We are counting depth in terms of Node, if the question was given in terms of edges then the answer will be 0 in the above case.

Disclaimer: Don’t jump directly to the solution, try it out yourself first.

Intuition + Approach: Using LEVEL ORDER TRAVERSAL

If we observe carefully, the depth of the Binary Tree is the number of levels in the binary tree. So, if we simply do a level order traversal on the binary tree and keep a count of the number of levels, it will be our answer.

In this example, if we start traversing the tree level-wise, then we can reach at max Level 4, so our answer is 4. Because the maximum depth we can achieve is indicated by the last level at which we can travel.

Java Code

public class tUf < private static int levelOrder( TreeNode root )< if( root == null )< return 0; >LinkedList queue = new LinkedList<>(); queue.addLast(root); int level = 0; while( queue.size() > 0 ) < int size = queue.size(); while( size-- >0 ) < TreeNode remNode = queue.removeFirst(); if( remNode.left != null )< queue.addLast( remNode.left ); >if( remNode.right != null ) < queue.addLast( remNode.right ); >> level++; > return level; > > 

Time Complexity: O(N)

Space Complexity: O(N) ( Queue data structure is used )

Intuition: Recursively ( Post Order Traversal )

If we have to do it recursively, then what we can think of is, If I have Maximum Depth of Left subtree and Maximum Depth of Right subtree then what will be the height or depth of the tree?

1 + max(depth of left subtree, depth of right subtree)

So, to calculate the Maximum Depth, we can simply take the maximum of the depths of the left and right subtree and add 1 to it.

Why take Maximum?? Because we need maximum depth so if we know left & right children’s maximum depth then we’ll definitely get to the maximum depth of the entire tree.

• We start to travel recursively and do our work in Post Order.
• Reason behind using Post Order comes from our intuition , that if we know the result of left and right child then we can calculate the result using that.
• This is exactly an indication of PostOrder, because in PostOrder we already calculated results for left and right children than we do it for current node.
• So for every node post order, we do Max( left result , right result ) + 1 and return it to the previous call.
• Base Case is when root == null so we need to return 0;

In Post Order, we start to travel on the example given in the below diagram

• Reach on Node 10 , Left child = null so 0 , Right child = null so 0 & add 1 for node 10 so max depth till node 10 is max(0,0) + 1 = 1.
• Reach on Node 2 , Left child = null so 0 , Right child = will give 1 & add 1 for node 2 so max depth till node 2 is max(0,1) + 1 = 2.
• Reach on Node 8 , Left child = null so 0 , Right child = null so 0 & add 1 for node 8 so max depth till node 8 is max(0,0) + 1 = 1.
• Reach on Node 11 , Left child = null so 0 , Right child = null so 0 & add 1 for node 11 so max depth till node 11 is max(0,0) + 1 = 1.
• Reach on Node 3 , Left child will give 1 , Right child = will give 1 & add 1 for node 3 so max depth till node 3 is max(1,1) + 1 = 2.
• Reach on Node 4 , Left child = null so 0 , Right child = null so 0 & add 1 for node 4 so max depth till node 4 is max(0,0) + 1 = 1.
• Reach on Node 5 , Left child will give 2 , Right child = will give 1 & add 1 for node 5 so max depth till node 5 is max(2,1) + 1 = 3.
• Reach on Node 12 , Left child will give 2 , Right child = will give 3 & add 1 for node 12 so max depth till node 12 is max(2,3) + 1 = 4.
• Hence 4 is our final ans.

C++ Code

class Solution < public: int maxDepth(TreeNode* root) < if(root == NULL) return 0; int lh = maxDepth(root->left); int rh = maxDepth(root->right); return 1 + max(lh, rh); > >;

Java Code

Time Complexity: O(N)

Space Complexity: O(1) Extra Space + O(H) Recursion Stack space, where “H” is the height of the binary tree.

Special thanks to Rishabh Goyal for contributing to this article on takeUforward. If you also wish to share your knowledge with the takeUforward fam, please check out this article

Источник