Matrix program in cpp

Saved searches

Use saved searches to filter your results more quickly

You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. Reload to refresh your session. You switched accounts on another tab or window. Reload to refresh your session.

Simple Matrix/Vector implementation on C++

pavel-shvetsov/matrix-cpp

This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.

Name already in use

A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?

Sign In Required

Please sign in to use Codespaces.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching Xcode

If nothing happens, download Xcode and try again.

Launching Visual Studio Code

Your codespace will open once ready.

There was a problem preparing your codespace, please try again.

Latest commit

Git stats

Files

Failed to load latest commit information.

README.md

Simple C++ Matrix impementation

sudo apt-get update sudo apt-get install build-essential git cmake cd ~/ git clone https://github.com/pavel-shvetsov/matrix-cpp.git mkdir matrix-cpp/build && cd matrix-cpp/build cmake .. && make ./matrix

Basic usage example could be seen in main.cpp source file

There are two classes test::mat and test::vec for matrix and vector objects respectively.

• Rows/Cols number for mat (zero-initialization): test::mat m(2,3)
• Elements number for vec (zero-initialization): test::vec v(8)
• 2d Initializer list for matrices: test::mat m< , >
• 1d Initializer list for matrices: test::vec v
• Copy constructor: test::mat B(test::mat &A)

• Matrix-matrix, matrix-vector multiplication: mat3 = mat1 * mat2 , mat2 = mat1 * vec1
• Matrix-matrix addition: mat3 = mat1 + mat2
• Scalar multiplication for both matrix and vector: mat2 = scalar * mat1 , vec2 = vec1 * scalar
• Subscript read/write: mat[row][col] , vec[idx]
• Standard output: std::cout

• Vectors are by default vertical
• No transpose operation is supported
• No linear algebra functions are supported, like inverse , determinant , svd , etc.

About

Simple Matrix/Vector implementation on C++

Источник

Saved searches

Use saved searches to filter your results more quickly

You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. Reload to refresh your session. You switched accounts on another tab or window. Reload to refresh your session.

Matrix Library is a C++ library for matrix operations such as addition, subtraction, multiplication, transpose, and more. It provides a Matrix class with constructors, destructors, and overloaded operators. The library can be built using CMake and depends on the Google Test framework for unit testing.

License

Astrodynamic/Matrix-Library-in-CPP

This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.

Name already in use

A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?

Sign In Required

Please sign in to use Codespaces.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching Xcode

If nothing happens, download Xcode and try again.

Launching Visual Studio Code

Your codespace will open once ready.

There was a problem preparing your codespace, please try again.

Latest commit

Git stats

Files

Failed to load latest commit information.

README.md

This is a C++ library that provides a Matrix class with various matrix operations, such as addition, subtraction, multiplication, and more.

To build the project, you can use CMake. Here are the steps to build the project:

1. Clone the repository to your local machine.
2. Navigate to the project directory
3. Run make

Reusing and Compiling with Other Projects

To use this library in your own C++ project, simply link against the Matrix.a library file generated in the lib directory.

This project depends on the Google Test framework for unit testing. CMake will download and build this dependency automatically when building the project.

To run the unit tests for this library, navigate to the build directory and run the following command:

There is a brief description of the matrix operations below that need to be implemented in the developing library. They are similar to the operations you performed earlier in «structured programming», so you can see a more detailed description of them there. Note that some operations have exceptional situations that require special handling using the exception mechanism.

Operation	Description	Exceptional situations
bool eq_matrix(const Matrix& other)	Checks matrices for equality with each other
void sum_matrix(const Matrix& other)	Adds the second matrix to the current one	different matrix dimensions
void sub_matrix(const Matrix& other)	Subtracts another matrix from the current one	different matrix dimensions
void mul_number(const double num)	Multiplies the current matrix by a number
void mul_matrix(const Matrix& other)	Multiplies the current matrix by the second matrix	the number of columns of the first matrix is not equal to the number of rows of the second matrix
Matrix transpose()	Creates a new transposed matrix from the current one and returns it
Matrix calc_complements()	Calculates the algebraic addition matrix of the current one and returns it	the matrix is not square
double determinant()	Calculates and returns the determinant of the current matrix	the matrix is not square
Matrix inverse_matrix()	Calculates and returns the inverse matrix	matrix determinant is 0

Apart from those operations, you also need to implement constructors and destructors:

Method	Description
Matrix()	A basic constructor that initialises a matrix of some predefined dimension
Matrix(int rows, int cols)	Parametrized constructor with number of rows and columns
Matrix(const Matrix& other)	Copy constructor
Matrix(Matrix&& other)	Move constructor
~Matrix()	Destructor

And you also need to overload the following operators, partly corresponding to the operations above:

Operator	Description	Exceptional situations
+	Addition of two matrices	different matrix dimensions
—	Subtraction of one matrix from another	different matrix dimensions
*	Matrix multiplication and matrix multiplication by a number	the number of columns of the first matrix does not equal the number of rows of the second matrix
==	Checks for matrices equality ( eq_matrix )
=	Assignment of values from one matrix to another one
+=	Addition assignment ( sum_matrix )	different matrix dimensions
-=	Difference assignment ( sub_matrix )	different matrix dimensions
*=	Multiplication assignment ( mul_matrix / mul_number )	the number of columns of the first matrix does not equal the number of rows of the second matrix
(int i, int j)	Indexation by matrix elements (row, column)	index is outside the matrix

Here is an example of how to use the Matrix class to perform matrix operations:

This will create two matrices, set their values, multiply them, and print the resulting matrix.

Источник

Matrix Multiplication in C++

A matrix is a rectangular array of numbers that are arranged in the form of rows and columns. In C++, a matrix is a so-called 2D array, with the dimensions as m,n, where m represents the number of rows present in the array, and n represents the number of columns in the array. We can perform several operations on a matrix-like addition, subtraction, multiplication, division, transposing of a matrix, and finding the rank of a matrix.

Introduction to Matrix Multiplication in C++

In our high school days, we learned about matrices and that we could perform some operations on the matrix. One of the operations was multiplying 2 matrices regardless of shape.

There are a few points to remember before the multiplication of the 2 matrices.

1. If matrix M1 with the shape of (m,n) and matrix M2 with the shape of (p,q), then for multiplication of M1 and M2, it is mandatory that n must be equal to p.
2. After calculating the multiplication of M1 and M2, the resultant matrix M3 will have a shape of (m,q).

The above 2 points must keep in mind during the matrix multiplication.

Before getting into the idea of calculating the matrix, let’s recall how we have calculated the matrix in mathematics on paper.

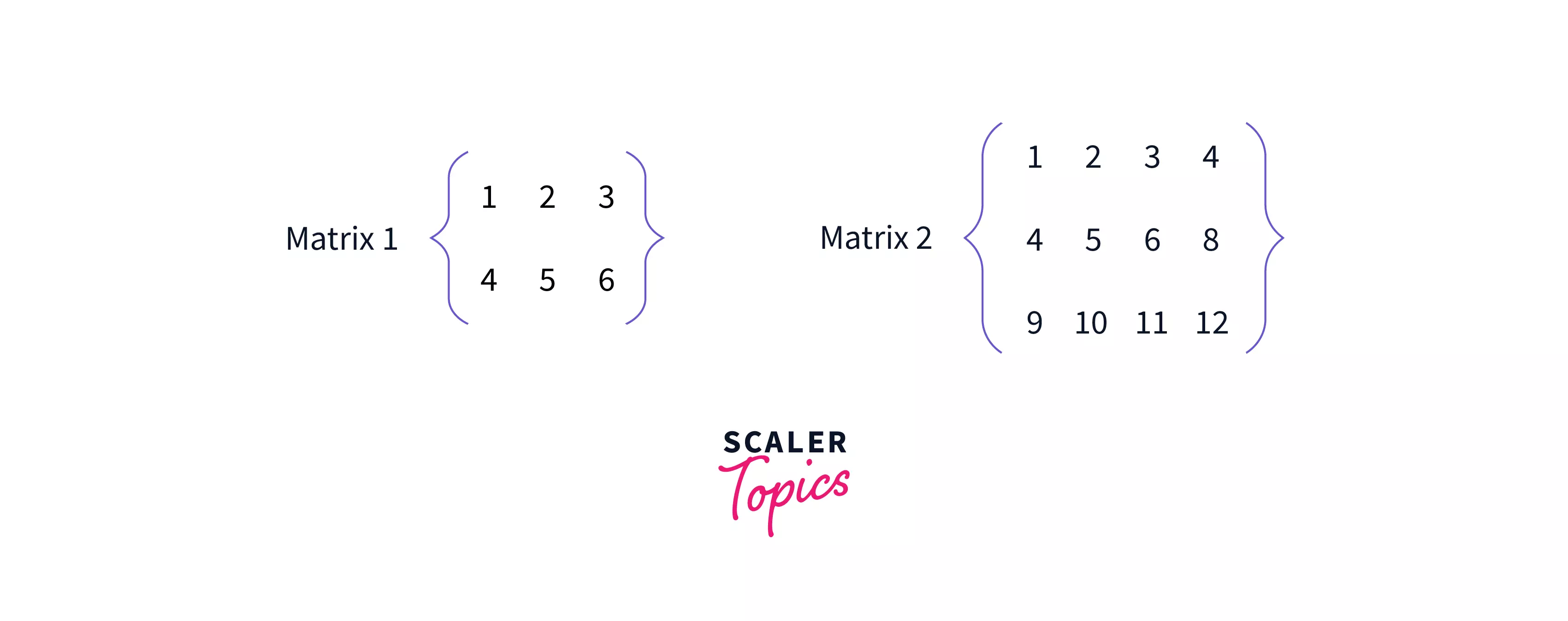
Suppose we have two matrices, M1 and M2, with shapes (2,3) and (3,4).

From the above 2 points, we can conclude that the (n=3) and (p=3) are equal, so matrix multiplication is valid. Now, we can also conclude the shape of the resultant matrix, i.e., M3 will be (2,4).

Now, we have to declare both the matrix and make assumptions using above mentioned two points. Now, we will multiply M1 and M2 to get our M3.

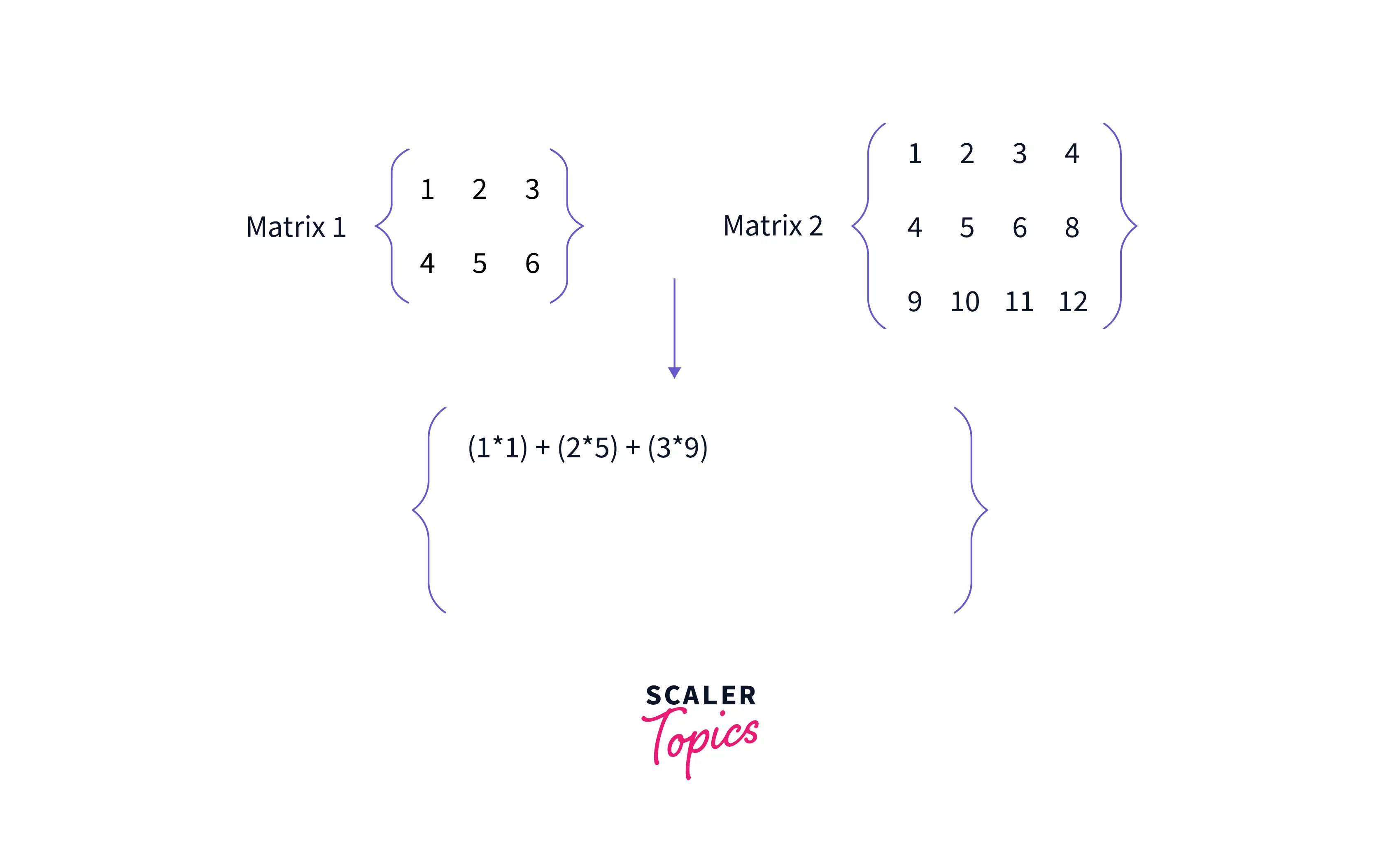
1. For every row in M1 and every column in M2. Multiply each element of the row of M1 with the column of M2, and add the elements.

First row of M1 is [1,2,3], and first column of M2 is [1,5,9]. Multiply each element with each other, so the resultant will be [1 * 1, 2 * 5, 3 * 9], and now add all the three elements, i.e., to form a single element. This resultant element will be the first element of our resultant M3 matrix. [(1 * 1) + (2 * 5) + (3 * 9)] = [1+ 10 + 27] => 38.

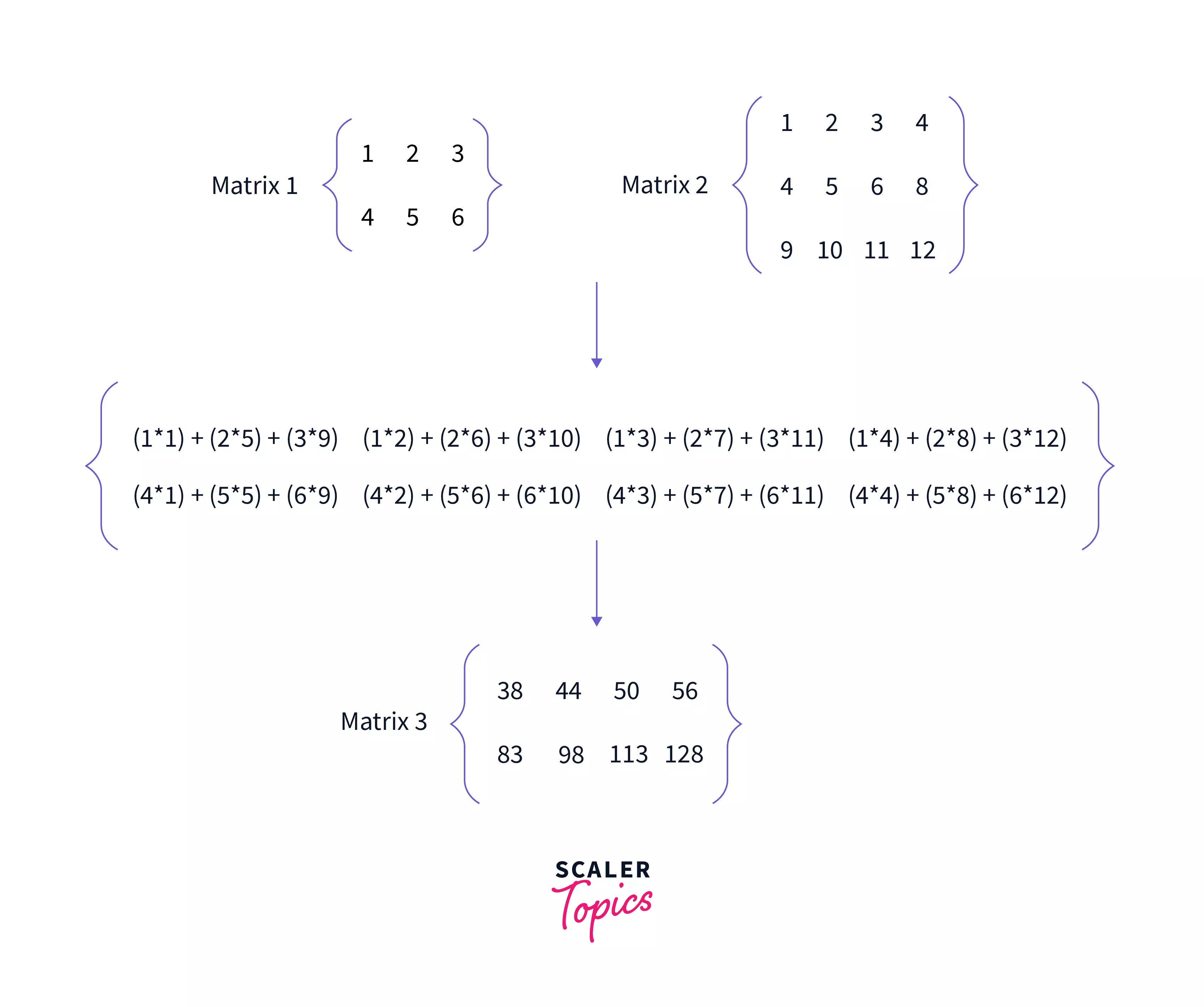
We will continue this process till we cover all the rows with all the columns.

We have continued our process till we haven’t covered all the rows in M1 and all the columns in M2. Now, we can see that the shape of matrix M3 is (2,4). Hence our above two mentioned points come up to be true.

The above case is what we have done in mathematics. But in this article, we have to write the code to multiply two matrices. The process of writing code is also the same. We will follow the same steps in writing code also.

Multiplication of Square Matrices (program)

Let us consider that we have a 2 square matrix, i.e., with the number of rows equal to the number of columns.

In the above code, we have created two matrices, matrix1 with shape (3,3) and matrix2 with shape (3,3).

CODE TO MULTIPLY 2 SQUARE MATRICES.

Time Complexity: O ( n 3 ) O(n^3) O ( n 3 ) The Time Complexity of the multiplication of Square Matrices is O ( n 3 ) O(n^3) O ( n 3 ) because we use 3 for loops that continue for all rows and columns, i.e., N. So, its complexity will be O ( n 3 ) O(n^3) O ( n 3 ) .

Auxiliary Space: O ( n 2 ) O(n^2) O ( n 2 ) We store a 2D array for the resultant matrix, which takes O ( n 2 ) O(n^2) O ( n 2 ) auxiliary space.

Multiplication of Rectangular Matrices (program)

Let us consider that we have two rectangular matrices, i.e., with the number of columns of matrix1 equal to the number of rows of matrix2.

CODE TO MULTIPLY 2 RECTANGULAR MATRICES

In the case of a Rectangular matrix, we will have Time Complexity as O(m * n * q) or O(m * p * q).

Auxilliary Space: O(m * q) because our new matrix m3 is of size (m, q), m rows, and q columns, so it requires m * q space.

Conclusion

• In this article, matrix multiplication in C++, we learned how to multiply two matrices.
• We have 2 cases for matrix multiplication(if both are matrix are square and both the matrices are rectangles). The square matrix multiplication is a special case of rectangular matrix multiplication.
• Next, we have to assume two things that are most likely to happen while the multiplication of the matrix, i.e.,
  • If matrix M1 has shape (m,n) and matrix M2 has shape (p,q), then n must be equal to p for multiplication of both the matrices.
  • If the matrices M1(m,n), and M2(p,q), then the shape of the resultant matrix multiplication, M3, will have shape(m,q).
  • Square Matrix
    • Time Complexity : O ( n 3 ) O(n^3) O ( n 3 )
    • Space Complexity : O ( n 2 ) O(n^2) O ( n 2 )
    • Time Complexity : O ( m ∗ n ∗ q ) O(m * n * q) O ( m ∗ n ∗ q ) or O ( m ∗ p ∗ q ) O(m * p * q) O ( m ∗ p ∗ q )
    • Space Complexity : O ( m ∗ q ) O(m * q) O ( m ∗ q )

    Источник