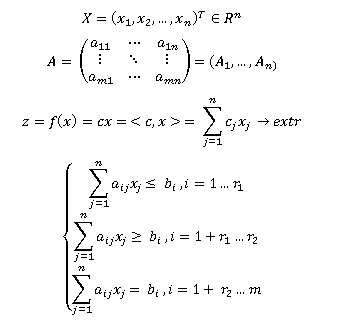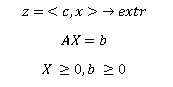Матричный метод решения задач линейного программирования

Подробный разбор симплекс-метода

Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему. Об этом, собственно, и поговорим.

Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.

§1. Постановка задачи линейного программирования

Определение: Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.

Общая задача линейного программирования (далее – ЛП) имеет вид:

§2. Каноническая форма задачи ЛП

Каноническая форма задачи ЛП:

Замечание: Любая задача ЛП сводится к канонической.

Алгоритм перехода от произвольной задачи ЛП к канонической форме:

1. Неравенства с отрицательными умножаем на (-1).
2. Если неравенство вида (≤), то к левой части добавляем – добавочную переменную, и получаем равенство.
3. Если неравенство вида (≥), то из левой части вычитаем , и получаем равенство.
4. Делаем замену переменных:

• Если , то
• Если — любой, то , где

§3. Угловые точки. Базисные/свободные переменные. Базисные решения

Определение: Точка называется угловой точкой, если представление возможно только при .

Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит (т.е. – не внутренняя точка).

Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.

§4. Симплекс-метод

Симплекс-метод позволяет эффективно найти оптимальное решение, избегая простой перебор всех возможных угловых точек. Основной принцип метода: вычисления начинаются с какого-то «стартового» базисного решения, а затем ведется поиск решений, «улучшающих» значение целевой функции. Это возможно только в том случае, если возрастание какой-то переменной приведет к увеличению значения функционала.

Необходимые условия для применения симплекс-метода:

Замечание: Базисный вектор имеет размерность (m*1), где m – количество уравнений в системе ограничений.

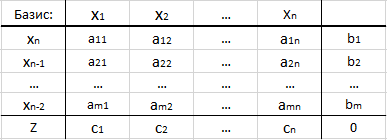
Для удобства вычислений и наглядности обычно пользуются симплекс-таблицами:

• В первой строке указывают «наименование» всех переменных.
• В первом столбце указывают номера базисных переменных, а в последней ячейке – букву Z (это строка функционала).
• В «середине таблицы» указывают коэффициенты матрицы ограничений — aij.
• Последний столбец – вектор правых частей соответствующих уравнений системы ограничений.
• Крайняя правая ячейка – значение целевой функции. На первой итерации ее полагают равной 0.

Замечание: Если ограничения в исходной задаче представлены неравенствами вида ≤, то при приведении задачи к канонической форме, введенные дополнительные переменные образуют начальное базисное решение.

Замечание: Коэффициенты в строке функционала берутся со знаком “-”.

Алгоритм симплекс-метода:

1. Выбираем переменную, которую будем вводить в базис. Это делается в соответствии с указанным ранее принципом: мы должны выбрать переменную, возрастание которой приведет к росту функционала. Выбор происходит по следующему правилу:

• Если задача на минимум – выбираем максимальный положительный элемент в последней строке.
• Если задача на максимум – выбираем минимальный отрицательный.

Замечание: Хотя мы и берем минимальное отрицательное число в задаче на максимум, этот коэффициент показывает направление роста функционала, т.к. строка функционала в симплекс-таблице взята со знаком “-”. Аналогичная ситуация с минимизацией.

Определение: Столбец симплекс-таблицы, отвечающий выбранному коэффициенту, называется ведущим столбцом.

2. Выбираем переменную, которую будем вводить в базис. Для этого нужно определить, какая из базисных переменных быстрее всего обратится в нуль при росте новой базисной переменной. Алгебраически это делается так:

• Вектор правых частей почленно делится на ведущий столбец
• Среди полученных значений выбирают минимальное положительное (отрицательные и нулевые ответы не рассматривают)

Замечание: Фактически, мы выражаем старые базисные переменные из каждого уравнения системы ограничений через остальные переменные и смотрим, в каком уравнении возрастание новой базисной переменной быстрее всего даст 0. Попадание в такую ситуацию означает, что мы «наткнулись» на новую вершину. Именно поэтому нулевые и отрицательные элементы не рассматриваются, т.к. получение такого результата означает, что выбор такой новой базисной переменной будет уводить нас из области, вне которой решений не существует.

3. Ищем элемент, стоящий на пересечении ведущих строки и столбца.

Определение: Такой элемент называется ведущим элементом.

4. Вместо исключаемой переменной в первом столбце (с названиями базисных переменных) записываем название переменной, которую мы вводим в базис.

5. Далее начинается процесс вычисления нового базисного решения. Он происходит с помощью метода Жордана-Гаусса.

• Новая Ведущая строка = Старая ведущая строка / Ведущий элемент
• Новая строка = Новая строка – Коэффициент строки в ведущем столбце * Новая Ведущая строка

6. После этого проверяем условие оптимальности. Если полученное решение неоптимально – повторяем весь процесс снова.

§5. Интерпретация результата работы симплекс-метода

Условие оптимальности полученного решения:

• Если задача на максимум – в строке функционала нет отрицательных коэффициентов (т.е. при любом изменении переменных значение итогового функционала расти не будет).
• Если задача на минимум – в строке функционала нет положительных коэффициентов (т.е. при любом изменении переменных значение итогового функционала уменьшаться не будет).

Однако, стоит отметить, что заданный функционал может не и достигать максимума/минимума в заданной области. Алгебраический признак этого можно сформулировать следующим образом:

При выборе ведущей строки (исключаемой переменной) результат почленного деления вектора правых частей на ведущий столбец содержит только нулевые и отрицательные значения.

Фактически, это значит, что какой бы рост мы не задавали новой базисной переменной, мы никогда не найдем новую вершину. А значит, наша функция не ограничена на множестве допустимых решений.

3. Альтернативные решения

При нахождении оптимального решения возможен еще один вариант – есть альтернативные решения (другая угловая точка, дающая то же самое значение функционала).

Алгебраический признак существования альтернативы:

После достижения оптимального решения имеются нулевые коэффициенты при свободных переменных в строке функционала.

Это значит, что при росте соответствующей переменной с нулевым коэффициентом значение функционала не изменится и новое базисное решение будет также давать оптимум функционала.

Эпилог

Данная статья направлена на более глубокое понимание теоретической части. В замечаниях и пояснениях здесь можно получить ответы на вопросы, которые обычно опускают при изучении этого метода и принимают априори. Однако, надо понимать, что многие методы численной оптимизации основаны на симплекс-методе (например, метод Гомори, М-Метод) и без фундаментального понимания вряд ли получится сильно продвинуться в дальнейшем изучении и применении всех алгоритмов этого класса.

Чуть позже напишу статью о практической реализации симплекс-метода, а также несколько статей о Методе искусственных переменных (М-Метод), Методе Гомори и Методе ветвей и границ.

Если уже сейчас Вы мучаетесь с реализацией симплекс-метода, советую почитать книгу А. Таха Введение в исследование операций — там все неплохо разобрано и в теории, и на примерах; а также посмотрите примеры решения задач matburo.ru — это поможет с реализацией в коде.

Источник

5.3.3 Решение матричных игр методами линейного программирования

Представленные выше примеры решение игры со смешенными стратегиями наглядно иллюстрируют теоретические положения матричных игр и трудоемкость ручного счета даже при матрице 2х2. Для авоматизации расчетов можно использовать программные продукты , метод расчета в которых основан на решении системы линейных уравнений http://www.uchimatchast.ru/.

Любую конечную игру двух лиц с нулевой суммой можно представить в виде задачи линейного программирования. При этом возможно решение задачи как с чистыми так со смешенными стратегиями. В случае чистых стратегий вероятность одной из стратегий будет равна единице, а вероятность остальных стратегий ,естественно, равна нулю.

Оптимальные значения вероятностей стратегийигрока А могут быть определены путем решения следующей максиминной задачи.

Сформулируем задачу матричной игры. Две конкурирующие компании А и B выпускают продукцию. Для увеличения продаж товар поставляется в различных упаковках. Компания А использует картон А₁, целлофан А₂, пластмасс А₃. Компания B использует такие же материалы для упаковки. Однако, при этом компании использовали различные виды оформления упаковок. В компании А зафиксировали увеличение/уменьшение притока покупателей в зависимости от упаковки товара и стратегии поведения конкурента B. Эти статистические данные представлены в таблице.

Решение задачи основано на получение наилучшего результата из наихудших для каждого игрока, который может быть получен определенной стратегии поведения. Из представленной таблицы следует, что данную задачу нельзя решить на основе чистых стратегий (седловой точки нет). Решение задачи находится между -2 и 2. В данном случае присутствуют смешенные стратегии, а так как количество стратегий у игрока А равно трем эту задачу можно решить с помощью линейного программирования (ЛП) алгебраическим методом. Следует заметить, что эту задачу нельзя решить графическим методом, так как количество стратегий у каждого игрока больше двух.

В соответствии с данными, представленными в таблице, задача ЛП для игрока А записывается следующим образом

максимизировать: (максимальное количество клиентов) при выполнении следующих ограничений:

5.3.3.1 Решение задачи лп симплекс-методом

Приведем систему ограничений к каноническому виду, для этого необходимо неравенства преобразовать в равенства, с добавлением дополнительных переменных. Если в преобразуемом неравенстве стоит знак ≥, то при переходе к равенству знаки всех его коэффициентов и свободных членов меняются на противоположные. Тогда система запишется в виде:

Переходим к формированию исходной симплекс таблицы. В строку F таблицы заносятся коэффициенты целевой функции. Так как нам необходимо найти максимум целевой функции, то в таблицу заносятся коэффициенты с противоположным знаком

Так как среди исходного набора условий были равенства, мы ввели искусственные переменные R. Это значит, что в симплекс таблицу нам необходимо добавить дополнительную строку M, элементы которой рассчитываются как сумма соответствующих элементов условий-равенств (тех которые после приведения к каноническому виду содержат искусственные переменные R) взятая с противоположным знаком.

Из данных задачи составляем исходную симплекс таблицу.

Источник