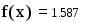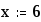Mathcad программирование разветвляющихся алгоритмов

2. Обращение к программе-функции Mathcad

Для выполнения программы-функции необходимо обратиться к имени программы-функции с указанием списка фактических параметров (если в описании программы присутствует список формальных параметров), т.е.

< имя - программы >( список фактических параметров )

Фактические параметры указывают, при каких конкретных значениях осуществляются вычисления в теле программы. Фактические параметры отделяются друг от друга запятой.

Очевидно, что между фактическими и формальными параметрами должно быть соответствие по количеству, порядку следования и типу. Последнее соответствие означает:

• если формальным параметром является простая переменная, то в качестве фактического может использоваться константа, переменная, арифметическое выражение;
• если формальным параметром является вектор или матрица, то фактическим должен быть вектор или матрица;
• если формальным параметром является имя встроенной функции или другой программы, то и фактическим параметром должен являться тот же объект.

Замечание Обращение к программе-функции должно находиться после описания программы-функции и к моменту обращенияфактические параметры должны быть определены.Пример 1. Обращение к программе f(x), приведенной на рис. 3 может иметь следующий вид:  Заметим, что переменная z никак не связана с “локальной” переменной z, используемой внутри тела программы-функции. Замечание Передать данные внутрь программы-функции можно используя внутри программы переменные, определенные до описания программы-функции. Например: Вызов программы Берется значение равное 2 Хотя значение переменной х изменилось внутри программы-функции, вне описания программы-функции эта переменная сохранила свое прежнее значение. Замечание Имена фактических параметров при вызове программы-функции могут не совпадать с именами ее формальных параметров.

3. Программирование в программе-функции линейных алгоритмов

Под линейным алгоритмом понимается вычислительный процесс, в котором необходимые операции выполняются строго последовательно. Операторы, реализующие этот алгоритм в теле программы — функции также размещаются последовательно и выполняются все, начиная с первого оператора и кончая последним. Пример 2. Оформим в виде программы-функции вычисление корней квадратного уравнения ax 2 + bx +c = 0 по формуле 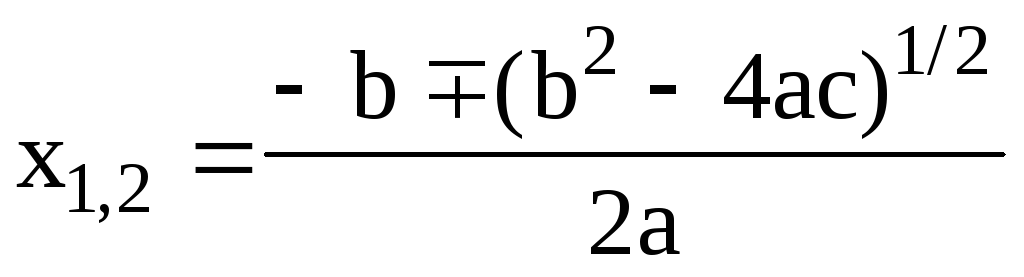Для этого введем следующее описание программы-функции Программа qq1 имеет четыре параметра: смысл первых трех понятен, а четвертый определяет знак перед корнем квадратным — задавая Sig1=1, получаем корень x₁; Sig1= — 1, получаем корень x₂. Программа реализует линейный алгоритм — все операторы выполняются всегда строго последовательно.

4. Программирование в программе-функции разветвляющихся алгоритмов

В разветвляющихся алгоритмах присутствует несколько ветвей вычислительного процесса. Выбор конкретной ветви зависит от выполнения (или невыполнения) заданных условий на значения переменных алгоритма. Пример 3. Переменная y задается следующим выражением y(х) = Видно, что алгоритм вычислений содержит две ветви и выбор зависит от значения переменной x. Для программирования разветвляющихся алгоритмов в Mathcad имеется условная функция if и условный оператор. Используя эти конструкции можно «изменить» последовательное выполнение операторов. В этих конструкциях могут использоваться следующие новые понятия. Выражения отношений. Эти выражения используются для сравнения двух арифметических выражений между собой. Выражение отношений записываются в виде : < выр. А >< знак отношения >< выр. В>, где в качестве знака отношения выступают символы, приведенные в таблице 1. Если заданное отношение выполняется, то выражение отношений принимает значение равное 1 ( «истина» ), в противном случае — 0 ( «ложь»).

Знак отношения	Вводимые символы
=	[ Ctrl ] + [ = ]
	[ < ]
>	[ > ]
	[ Ctrl ] + [ 0 ]
	[ Ctrl ] + [ 9 ]
	[ Ctrl ] + [ 3 ]

Таблица 1 Пример 4. Вычисление выражения отношений _{Результат вычисления выражения отношений}В отличие от языков программирования можно сразу в одном выражении проверять несколько условий путем добавления знаков отношений и арифметических выражений. Эту возможность иллюстрирует следующий пример. Пример 5.Логические операции. Определены две логических операции, которые ставятся между выражениями отношений. Логическая операция ИЛИ. Обозначается знаком + и записывается в виде < логич.выр.1 >+ < логич.выр. 2>Результат операции равен 0, если оба логических выражения равны 0 и равен 1 для всех остальных значений логических выражений. Логическая операция И. Вводится знаком * ( в тексте это точка ) и записывается в виде < логич.выр.1 >. < логич.выр. 2>Результат равен 1, если оба логических выражения равны 1 и равен 0 для всех остальных значений логических выражений Логическое выражение. Логическим выражением называется конструкция, составленная из выражений отношений, знаков логических операций и круглых скобок. Значение логического выражения вычисляется слева направо с учетом известного правила о приоритете операций. Список приоритетов ( по их убыванию ):

• круглые скобки;
• логическая операция И;
• логическая операция ИЛИ.

Условная функция if. Эта функция записывается в виде : if ( < логич. выраж. >, < ариф.выраж.1>, < ариф.выраж.2 >) Правило вычисления условной функцииif : если логическое выражение равно 1, то функция принимает значение равное значению арифметического выражения 1; если логическое выражение равно 0, то функция принимает значение равное значению арифметического выражения 2. Условная функция используется в арифметических выражениях, стоящих в правой части локального оператора присваивания. Пример 6. Реализуем алгоритм вычисления функции y(х) примера 3 в виде Обращение к этой программе-функции в тексте документа Условный оператор. Этот оператор используется только в теле программы-функции и для его ввода необходимо щелкнуть на кнопке if панели программирования. На экране появляется конструкция с двумя полями ввода, изображенная на следующем рисунке. Поле 2 Поле 1 В поле 2 вводится логическое выражение (в простейшем случае это выражение отношений). В поле 1 вводится выражение (как правило, арифметическое), значение которого используется, если проверяемое логическое выражение принимает значение 1. Например: Поле 2 Поле 1 Поле 3 В поле 3 задается выражение, значение которого используется, если логическое выражение равно 0. Для ввода в поле 3 необходимо :

• заключить это поле в выделяющую рамку;
• щелкнуть на кнопке “otherwise” панели программирования;
• в оставшемся поле введите соответствующее выражение.

Пример 7. Составим программу-функцию, вычисляющую функцию y(x), заданную в примере 3. Для этого введем описание следующей программы-функции: Обращение к этой программе-функции имеет вид Таким образом, выражение, стоящее перед словом otherwise выполняется только в том случае, если не выполнено заданное перед этим условием. В программе можно использовать несколько следующих друг за другом условных операторов с одним выражением перед словом otherwise. Пример 8. Составим программу-функцию для вычисления переменной z по формуле z( t ) = В рабочий документ введем описание следующей программы-функции Заметим, что функция z(t) получит значение ln(t) только тогда, когда не выполняется условие записанные в двух вышестоящих строках. Обращение к этой программе — функции имеет вид  Если в поле 3 ввести оператор без слова otherwise, то этот оператор будет выполняться всегда вне зависимости от выполнения выше заданных условных операторов.

Источник

Реализация разветвляющихся алгоритмов в mathcad

MATHCAD – физико-математический пакет для решения прикладных задач, удобный в работе и простой по освоению [4, 5]. Графическая среда MATHCAD позволяет записывать математические формулы в привычном виде, результаты вычислений могут быть представлены как численно, так и аналитически (в виде формул).

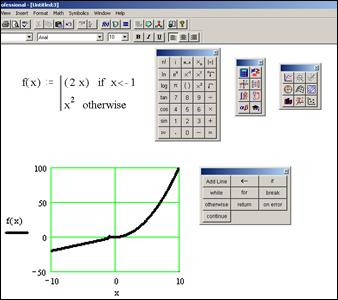
С помощью панели «Programming (программирование)» в MATHCAD можно реализовать вычисления и по разветвляющимся алгоритмам. Для создания программной строки понадобится команда «Add Line», для осуществления выбора по условию – команда «if» и команда «otherwise» — в остальных случаях (рис.7). График неэлементарной функции f(x) построен с помощью панели «Graph (Графики)».

Рис. 7. Программирование разветвляющихся алгоритмов в MATHCAD

ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ«Разработка алгоритмов для структурного программирования и их реализация. Часть 1: ветвление»

Этап 1. Постановка задачи 1. Разработать алгоритм, спецификацию, тестовый пример и программу, которая вычисляла бы значение функции:

Этап 2. Анализ. Программа должна начинаться с ввода значений аргумента. Затем, в зависимости от того, в какой интервал попадает введенное значение, вычисляется значение функции по одному из заданных выражений.

Этап 3. Проектирование и определение спецификаций.

Расчет тестовых примеров выполняем в MATHCAD (тесты должны быть определены таким образом, чтобы проверить все ветви программы, рис.8). Результаты расчетов занесены в табл. 1.

Рис. 8. Расчет тестовых примеров

Разветвляющийся алгоритм представлен на рис. 9. Спецификация к алгоритму – в табл. 2.

Рис. 9. Алгоритм решения задачи 1.

Тестовые примеры для задачи 1.

Номер теста	х	Результат у
-1 (x )
25 (x >8)

Спецификация к алгоритму на рис. 8.

Этап 1. Постановка задачи 2. Разработать алгоритм, спецификацию, тестовый пример и программу для вычисления температуры в зоне обработки по формуле , и проверить условие , где K – суммарный коэффициент условий обработки; S – подача станка, мм/об; n – число оборотов шпинделя станка, об.; t – глубина резания, мм; T_max – максимально возможная температура в зоне обработки, с точки зрения качества, °C; x,y,z – значения степеней, полученные экспериментальным путем.

Этап 2. Анализ. Алгоритм (программа) должен начинаться с ввода значений x, y, z, S, n, t, K, T_max. Затем, в зависимости от вычисленного значения температуры Т, выдается сообщение пользователю о выполнении или не выполнении поставленного условия.

Этап 3. Проектирование и определение спецификаций. Разветвляющийся алгоритм представлен на рис. 10.

Рис. 10. Алгоритм решения задачи 2.

Спецификация к алгоритму на рис. 10.

№	Наименование	Обозначение в алгоритме	Обозначение в программе	Ед. изм.	Статус переменной	Тип
Показатель степени	х	х	—	Входная	Веществ.
Показатель степени	у	у	—	Входная	Веществ.
Показатель степени	z	z	—	Входная	Веществ.
Cуммарный коэффициент условий обработки	K	K	—	Входная	Веществ.
Подача станка	S	S	мм/об	Входная	Веществ.
Число оборотов шпинделя станка	n	n	об.	Входная	Веществ.
Глубина резания	t	t	мм	Входная	Веществ.
Максимально допустимая температура	Tmax	Tmax	°С	Входная	Веществ.
Температура в зоне обработки	T	Tem	°С	Расчетная	Веществ.

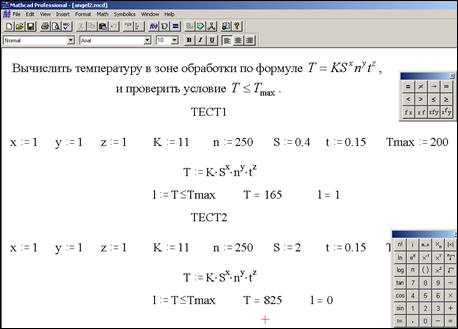
Тестовые (контрольные) примеры рассчитываем в MATHCAD (рис. 11). Тесты должны быть определены таким образом, чтобы проверить все ветви алгоритма (программы).

Рис. 11. Расчет тестовых примеров в MATHCAD для задачи 2

Знаки «£» и «³» для проверки неравенств находятся на панели MATHCAD «Boolean (булевое)». Результат проверки условия хранится в ячейке l, которая принимает значение «1», если условие выполняется (ТЕСТ1 на рис. 11), и принимает значение «0» при невыполнении условия (ТЕСТ2 на рис. 11). Результаты расчетов в MATHCAD занесены в табл. 4.

Тестовые примеры для задачи 2.

Номер теста	x	Y	z	K	n	S	t	Tmax	Результат (T)
1,0	1,0	1,0	11,0	0,4	0,15	Условие выполняется (T =165)
1,0	1,0	1,0	11,0	2,0	0,15	Условие не выполняется (T =825)

Источник