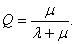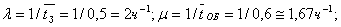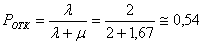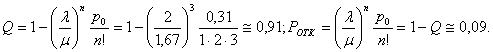Математическое программирование модели массового обслуживания

Математические модели простейших систем массового обслуживания

Ниже будут рассмотрены примеры простейших систем массового обслуживания (СМО). Понятие «простейшие» не означает «элементарные». Математические модели этих систем применимы и успешно используются в практических расчетах.

Одноканальная смо с отказами

Дано: система имеет один канал обслуживания, на который поступает простейший поток заявок с интенсивностью. Поток обслуживаний имеет интенсивность. Заявка, заставшая систему занятой, сразу же покидает ее.

Найти: абсолютную и относительную пропускную способность СМО и вероятность того, что заявка, пришедшая в момент времени t, получит отказ.

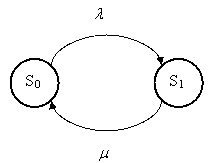
Система при любом t> 0 может находиться в двух состояниях:S₀– канал свободен;S₁– канал занят. Переход изS₀вS₁связан с появлением заявки и немедленным началом ее обслуживания. Переход изS₁вS₀осуществляется, как только очередное обслуживание завершится (рис.4).

Рис.4. Граф состояний одноканальной СМО с отказами

Выходные характеристики (характеристики эффективности) этой и других СМО будут даваться без выводов и доказательств.

Абсолютная пропускная способность(среднее число заявок, обслуживаемых в единицу времени):

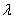
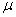
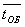
где – интенсивность потока заявок (величина, обратная среднему промежутку времени между поступающими заявками —);

–интенсивность потока обслуживаний (величина, обратная среднему времени обслуживания )

Относительная пропускная способность(средняя доля заявок, обслуживаемых системой):

Вероятность отказа(вероятность того, что заявка покинет СМО необслуженной):

Очевидны следующие соотношения: и.

Пример. Технологическая система состоит из одного станка. На станок поступают заявки на изготовление деталей в среднем через 0,5 часа. Среднее время изготовления одной детали равно. Если при поступлении заявки на изготовление детали станок занят, то она (деталь) направляется на другой станок. Найти абсолютную и относительную пропускную способности системы и вероятность отказа по изготовлению детали.

Т.е. в среднем примерно 46 % деталей обрабатываются на этом станке.

.

Т.е. в среднем примерно 54 % деталей направляются на обработку на другие станки.

N – канальная смо с отказами (задача Эрланга)

Это одна из первых задач теории массового обслуживания. Она возникла из практических нужд телефонии и была решена в начале 20 века датским математиком Эрлангом.

Дано: в системе имеетсяn– каналов, на которые поступает поток заявок с интенсивностью. Поток обслуживаний имеет интенсивность. Заявка, заставшая систему занятой, сразу же покидает ее.

Найти: абсолютную и относительную пропускную способность СМО; вероятность того, что заявка, пришедшая в момент времениt, получит отказ; среднее число заявок, обслуживаемых одновременно (или, другими словам, среднее число занятых каналов).

Решение. Состояние системыS(СМО) нумеруется по максимальному числу заявок, находящихся в системе (оно совпадает с числом занятых каналов):

• S₀– в СМО нет ни одной заявки;
• S₁– в СМО находится одна заявка (один канал занят, остальные свободны);
• S₂– в СМО находится две заявки (два канала заняты, остальные свободны);
• . . .
• S_n– в СМО находитсяn– заявок (всеn– каналов заняты).

Граф состояний СМО представлен на рис. 5 Рис.5 Граф состояний для n – канальной СМО с отказами Почему граф состояний размечен именно так? Из состояния S₀в состояниеS₁систему переводит поток заявок с интенсивностью(как только приходит заявка, система переходит изS₀вS₁). Если система находилась в состоянииS₁и пришла еще одна заявка, то она переходит в состояниеS₂и т.д. Почему такие интенсивности у нижних стрелок (дуг графа)? Пусть система находится в состоянии S₁(работает один канал). Он производитобслуживаний в единицу времени. Поэтому дуга перехода из состоянияS₁в состояниеS₀нагружена интенсивностью. Пусть теперь система находится в состоянииS₂(работают два канала). Чтобы ей перейти вS₁, нужно, чтобы закончил обслуживание первый канал, либо второй. Суммарная интенсивность их потоков равнаи т.д. Выходные характеристики (характеристики эффективности) данной СМО определяются следующим образом. Абсолютнаяпропускнаяспособность: где n– количество каналов СМО; –вероятность нахождения СМО в начальном состоянии, когда все каналы свободны (финальная вероятность нахождения СМО в состоянии S₀); Рис.6. Граф состояний для схемы «гибели и размножения» Для того, чтобы написать формулу для определения , рассмотрим рис.6 Граф, представленный на этом рисунке, называют еще графом состояний для схемы «гибели и размножения». Напишем сначала для общую формулу (без доказательства): Кстати, остальные финальные вероятности состояний СМО запишутся следующим образом. Вероятность того, что СМО находится в состоянии S₁, когда один канал занят: Вероятность того, что СМО находится в состоянии S₂, т.е. когда два канала заняты: Вероятность того, что СМО находится в состоянии S_n, т.е. когда все каналы заняты. Теперь для n – канальной СМО с отказами При этом Относительная пропускная способность: Напомним, что это средняя доля заявок, обслуживаемых системой. При этом ; . Вероятностьотказа: Напомним, что это вероятность того, что заявка покинет СМО необслуженной. Очевидно, что . Среднее число занятых каналов (среднее число заявок, обслуживаемых одновременно): При этом . Пример. Имеется технологическая система (участок), состоящая из трех одинаковых станков. В систему поступают для обработки детали в среднем через 0,5 часа (). Среднее время изготовления одной детали. Если при поступлении заявки на изготовление детали все станки заняты, то деталь направляется на другой участок таких же станков. Найти финальные вероятности состояний системы и характеристики (показатели эффективности) данной СМО. , т.е. в среднем две заявки на обработку деталей в час. . Граф состояний системы представлен на рис.7 Рис.7Граф состояний для рассматриваемого примера Возможные состояния системы: S₀– в СМО (на участке) нет ни одной заявки; S₁– в СМО (на участке) одна заявка; S₂– в СМО (на участке) две заявки; S₃– в СМО (на участке) три заявки (заняты все три станка). Вероятность того, что все станки свободны: Вероятность того, что один станок занят: Вероятность того, что два станка заняты: Вероятность того, что все три станка заняты: Т.е. в среднем в этой системе обрабатывается 1,82 дет/ч (примерно 91 % направляемых деталей), при этом примерно 9 % деталей направляется для обработки на другие участки. Одновременно в среднем работает в основном один станок ( ). Но из–за случайных характеристик потока заявок иногда работают одновременно все три станка (), отсюда 9 % отказов.

Источник

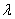
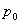
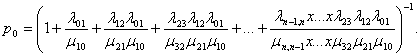
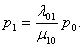
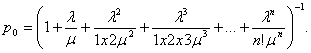
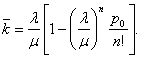
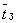
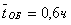
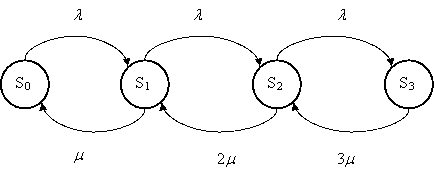
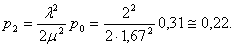
4. Моделирование систем массового обслуживания

4.1. Компоненты и классификация моделей массового обслуживания

Рассмотренный в п.2 марковский случайный процесс с дис­кретными состояниями и непрерывным временем имеет место в системах массового обслуживания.

Системы массового обслуживания — это такие системы, в кото­рые в случайные моменты времени поступают заявки на обслужи­вание, при этом поступившие заявки обслуживаются с помощью имеющихся в распоряжении системы каналов обслуживания.

С позиции моделирования процесса массового обслуживания ситуации, когда образуются очереди заявок (требований) на обслу­живание, возникают следующим образом. Поступив в обслуживаю­щую систему, требование присоединяется к очереди других (ранее поступивших) требований. Канал обслуживания выбирает требова­ние из находящихся в очереди, с тем чтобы приступить к его об­служиванию. После завершения процедуры обслуживания очеред­ного требования канал обслуживания приступает к обслуживанию следующего требования, если таковое имеется в блоке ожидания.

Цикл функционирования системы массового обслуживания подоб­ного рода повторяется многократно в течение всего периода рабо­ты обслуживающей системы. При этом предполагается, что пере­ход системы на обслуживание очередного требования после завер­шения обслуживания предыдущего требования происходит мгно­венно, в случайные моменты времени.

Примерами систем массового обслуживания могут служить:

• посты технического обслуживания автомобилей;
• посты ремонта автомобилей;
• персональные компьютеры, обслуживающие поступающие заяв­ки или требования на решение тех или иных задач;
• станции технического обслуживания автомобилей;
• аудиторские фирмы;
• отделы налоговых инспекций, занимающиеся приемкой и про­веркой текущей отчетности предприятий;
• телефонные станции и т. д.

• входной поток поступающих требований или заявок на обслужи­вание;
• дисциплина очереди;
• механизм обслуживания.

• первым пришел — первый обслуживаешься;
• пришел последним — обслуживаешься первым;
• случайный отбор заявок;

• отбор заявок по критерию приоритетности;

• вероятностным распределением моментов поступлений заявок на обслуживание (единичных или групповых);
• вероятностным распределением времени продолжительности об­служивания;
• конфигурацией обслуживающей системы (параллельное, после­довательное или параллельно-последовательное обслуживание);
• количеством и производительностью обслуживающих каналов;
• дисциплиной очереди;
• мощностью источника требований.

• вероятность немедленного обслуживания поступившей заявки;
• вероятность отказа в обслуживании поступившей заявки;
• относительная и абсолютная пропускная способность системы;
• средний процент заявок, получивших отказ в обслуживании;
• среднее время ожидания в очереди;
• средняя длина очереди;
• средний доход от функционирования системы в единицу време­ни и т.п.

• системы с отказами, в которых заявка, поступившая в систему в момент, когда все каналы заняты, получает отказ и сразу же по­кидает очередь;
• системы с ожиданием (очередью), в которых заявка, поступив­шая в момент, когда все каналы обслуживания заняты, стано­вится в очередь и ждет, пока не освободится один из каналов.

• длина очереди;
• время пребывания в очереди.

• одноканальные системы;
• многоканальные системы.

Источник