Математические основы программирования алгоритмы

ОСНОВЫ ПРОГРАММИРОВАНИЯ Раздел 2. Математические основы программирования Численные алгоритмы Старший преподаватель Кафедры ВС, к.т.н. Поляков Артем Юрьевич. — презентация

Презентация на тему: » ОСНОВЫ ПРОГРАММИРОВАНИЯ Раздел 2. Математические основы программирования Численные алгоритмы Старший преподаватель Кафедры ВС, к.т.н. Поляков Артем Юрьевич.» — Транскрипт:

1 ОСНОВЫ ПРОГРАММИРОВАНИЯ Раздел 2. Математические основы программирования Численные алгоритмы Старший преподаватель Кафедры ВС, к.т.н. Поляков Артем Юрьевич 1 © Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»

2 Рассматриваемые вопросы Примеры численных алгоритмов: – вычисление определенного интеграла функции одной переменной; 2 © Кафедра вычислительных систем ГОУ ВПО «СибГУТИ»

3 Геометрический смысл определенного интеграла 3 © Кафедра вычислительных систем ГОУ ВПО «СибГУТИ» f (x) ab x y Под определенным интегралом S понимают площадь подграфика функции f (x) на отрезке [a, b].

4 Приближенное вычисление определенного интеграла (метод левых прямоугольников) 4 © Кафедра вычислительных систем ГОУ ВПО «СибГУТИ» f (x) a b x y

5 Приближенное вычисление определенного интеграла (метод правых прямоугольников) 5 © Кафедра вычислительных систем ГОУ ВПО «СибГУТИ» f (x) a b x y

6 Приближенное вычисление определенного интеграла (метод прямоугольников) 6 © Кафедра вычислительных систем ГОУ ВПО «СибГУТИ» f (x) a b x y

7 Алгоритм метода прямоугольников 7 © Кафедра вычислительных систем ГОУ ВПО «СибГУТИ» f (x), a, b, N i = 0, S=0, h = (b a)/N НАЧАЛО i N 1 x = a + h·(i + 0,5) S = S + f (x)·h i = i + 1 КОНЕЦ НЕТ ДА S

8 Псевдокод алгоритма метода прямоугольников 8 © Кафедра вычислительных систем ГОУ ВПО «СибГУТИ» ввод f (x), N, a, b i = 0 S = 0 h = (b a)/N пока i N 1 делать x = a + h·(i + 0,5) S = S + f (x)·h i = i + 1 конец пока вывод S

9 Погрешность метода прямоугольников 9 © Кафедра вычислительных систем ГОУ ВПО «СибГУТИ» Точность метода зависит: 1.От длины интервала интегрирования (b – a). 2.От длины h шага приближенного интегрирования. 3.От функции f(x), которая представлена первой или второй производной. Единственный параметр, на который можно повлиять – это шаг h. Какой максимальной точности можно добиться при фиксированных остальных параметрах? — Метод левых и правых прямоугольников — Метод прямоугольников

10 Метод трапеций (приближение полиномами первой степени) 10 © Кафедра вычислительных систем ГОУ ВПО «СибГУТИ» xixi x i+1

11 Алгоритм метода трапеций 11 © Кафедра вычислительных систем ГОУ ВПО «СибГУТИ» f (x), N, a, b i = 0, S=0,h=(b a)/N НАЧАЛО i (N – 1) x 1 = a + h·i x 2 = a + h·(i + 1) S = S + ( f (x 1 ) + f (x 2 ))·h/2 i = i + 1 КОНЕЦ НЕТ ДА S

12 Псевдокод алгоритма метода трапеций 12 © Кафедра вычислительных систем ГОУ ВПО «СибГУТИ» ввод f (x), N, a, b i = 0 S = 0 h=(b a)/N пока i (N – 1) делать x 1 = a + h·i x 2 = x 1 + h S = S + ( f (x 1 ) + f (x 2 ))· h /2 i = i + 1 конец пока вывод S

13 Погрешность метода трапеций 13 © Кафедра вычислительных систем ГОУ ВПО «СибГУТИ» Точность метода зависит: 1.От длины интервала интегрирования (b – a). 2.От длины h шага приближенного интегрирования. 3.От функции f(x), которая представлена второй производной f»(x). Единственный параметр, на который можно повлиять – это шаг h. Какой максимальной точности можно добиться при фиксированных остальных параметрах?

14 14 © Кафедра вычислительных систем ГОУ ВПО «СибГУТИ» Метод Симпсона (приближение полиномом 2-й степени) xixi x i+1/2 xi+1xi+1

15 Алгоритм метода Симпсона 15 © Кафедра вычислительных систем ГОУ ВПО «СибГУТИ» f (x), N, a, b i = 0, S=0, h = (b a)/N НАЧАЛО i N 1 x i = a + h·i x i+1 = x i + h x i+1/2 = (x i + x i+1 )/2 S = S + ( f (x i ) +4 f (x i+1/2 )+ f (x i+1 ))·h/6 i = i + 1 КОНЕЦ НЕТ ДА S

16 Псевдокод алгоритма Симпсона 16 © Кафедра вычислительных систем ГОУ ВПО «СибГУТИ» ввод f (x), N, a, b i = 0 S = 0 h=(b a)/N пока i N – 1 делать x i = a + h·i x i+1 = x i + h x i+1/2 = (x i + x i+1 )/2 S = S + ( f (x i ) +4 f (x i+1/2 )+ f (x i+1 ))·h/6 i = i + 1 конец пока вывод S

17 Погрешность метода Симпсона 17 © Кафедра вычислительных систем ГОУ ВПО «СибГУТИ» Точность метода зависит: 1.От длины интервала интегрирования (b – a). 2.От длины h шага приближенного интегрирования. 3.От функции f(x), которая представлена третьей производной. Единственный параметр, на который можно повлиять – это шаг h. Какой максимальной точности можно добиться при фиксированных остальных параметрах?

18 ИТОГИ 18 © Кафедра вычислительных систем ГОУ ВПО «СибГУТИ» Рассмотрено 5 алгоритмов численного интегрирования и рассмотрены факторы, влияющие на точность их работы: 1.Метод левых прямоугольников 2.Метод правых прямоугольников 3.Метод и алгоритм прямоугольников (средних) 4.Метод трапеций 5.Метод Симпсона

Источник

1. Основы алгоритмизации

Этапы решения задачи на ЭВМ. Работа по решению любой задачи с использованием компьютера делится на следующие этапы:

1. Постановка задачи.
2. Формализация задачи.
3. Построение алгоритма.
4. Составление программы на языке программирования.
5. Отладка и тестирование программы.
6. Проведение расчетов и анализ полученных результатов.

Часто эту последовательность называют технологической цепочкой решения задачи на ЭВМ. Непосредственно к программированию в этом списке относятся пункты 3, 4, 5. На этапе постановки задачи должно быть четко сформулировано, что дано и что требуется найти. Здесь очень важно определить полный набор исходных данных, необходимых для получения решения. Второй этап — формализация задачи. Здесь чаще всего задача переводится на язык математических формул, уравнений, отношений. Если решение требует математического описания какого-то реального объекта, явления или процесса, то формализация равносильна получению соответствующей математической модели. Третий этап — построение алгоритма. Опытные программисты часто сразу пишут программы на языках, не прибегая к каким-либо специальным способам описания алгоритмов (блок-схемам, псевдокодам). Однако в учебных целях полезно использовать эти средства, а затем переводить полученный алгоритм на язык программирования. Первые три этапа предусматривают работу без компьютера. Дальше следует собственно программирование на определенном языке, в определенной системе программирования. Последний (шестой) этап — это использование уже разработанной программы в практических целях. Таким образом, программист должен обладать следующими знаниями и навыками:

• уметь строить алгоритмы;
• знать языки программирования;
• уметь работать в соответствующей системе программирования.

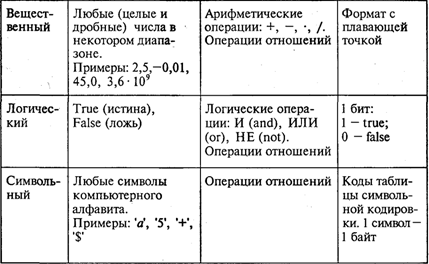
Основой программистской грамотности является развитое алгоритмическое мышление.Понятие алгоритма. Одним из фундаментальных понятий в информатике является понятие алгоритма. Происхождение самого термина «алгоритм» связано с математикой. Это слово происходит от Algorithm! — латинского написания имени Мухаммеда аль-Хорезми (787—850), выдающегося математика средневекового Востока. В XII в. был выполнен латинский перевод его математического трактата, из которого европейцы узнали о десятичной позиционной системе счисления и правилах арифметики многозначных чисел. Именно эти правила в то время называли алгоритмами. Сложение, вычитание, умножение столбиком, деление уголком многозначных чисел — вот первые алгоритмы в математике. Правила алгебраических преобразований, способы вычислений корней уравнений также можно отнести к математическим алгоритмам. В наше время понятие алгоритма трактуется шире. Алгоритм — это последовательность команд управления каким-либо исполнителем. В школьном курсе информатики с понятием алгоритма, с методами построения алгоритмов ученики знакомятся на примерах учебных исполнителей: Робота, Черепахи, Чертежника и т.д. Эти исполнители ничего не вычисляют. Они создают рисунки на экране, перемещаются в лабиринтах, перетаскивают предметы с места на место. Таких исполнителей принято называть исполнителями, работающими в обстановке. В разделе информатики под названием «Программирование» изучаются методы программного управления работой ЭВМ. Следовательно, в качестве исполнителя выступает компьютер. Компьютер работает с величинами — различными информационными объектами: числами, символами, кодами и т. п. Поэтому алгоритмы, предназначенные для управления компьютером, принято называть алгоритмами работы с величинами. Данные и величины. Совокупность величин, с которыми работает компьютер, принято называть данными. По отношению к программе данные делятся на исходные, результаты (окончательные данные) и промежуточные (рис. 1), которые получаются в процессе вычислений. Например, при решении квадратного уравнения ax2 + bx + с = 0 исходными данными являются коэффициенты а, b, с, результатами — корни уравнения х1, х2, промежуточным данным — дискриминант уравнения D = b2 — 4aс. Для успешного освоения программирования необходимо усвоить следующее правило: всякая величина занимает свое определенное место в памяти ЭВМ (иногда говорят — ячейку памяти). Хотя термин «ячейка» с точки зрения архитектуры современных ЭВМ несколько устарел, однако в учебных целях его удобно использовать. У всякой величины имеются три основных свойства: имя, значение и тип. На уровне команд процессора величина идентифицируется при помощи адреса ячейки памяти, в которой она хранится. В алгоритмах и языках программирования величины делятся на константы и переменные Константа — неизменная величина, и в алгоритме она представляется собственным значением, например: 15, 34.7, k, true и т.д. Переменные величины могут изменять свои значения в ходе выполнения программы и представляются символическими именами — идентификаторами, например: X, S2, codl5. Любая константа, как и переменная, занимает ячейку памяти, а значение этих величин определяется двоичным кодом в этой ячейке. Теперь о типах величин — типах данных. С понятием типа данных вы уже, возможно, встречались, изучая в курсе информатики базы данных и электронные таблицы. Это понятие является фундаментальным для программирования. В каждом языке программирования существует своя концепция типов данных, своя система типов. Тем не менее в любой язык входит минимально необходимый набор основных типов данных, к которому относятся: целый, вещественный, логический и символьный типы. С типом величины связаны три ее характеристики: множество допустимых значений, множество допустимых операций, форма внутреннего представления. В табл. 1.1 представлены эти характеристики основных типов данных. Таблица 1.1 Типы констант определяются по контексту (т. е. по форме записи в тексте), а типы переменных устанавливаются в описаниях переменных. Есть еще один вариант классификации данных — классификация по структуре. Данные делятся на простые и структурированные. Для простых величин (их еще называют скалярными) справедливо утверждение: одна величина — одно значение, для структурированных: одна величина — множество значений. К структурированным величинам относятся массивы, строки, множества и т.д. ЭВМ — исполнитель алгоритмов. Как известно, всякий алгоритм (программа) составляется для конкретного исполнителя в рамках его системы команд. О каком же исполнителе идет речь при обсуждении вопроса о программировании для ЭВМ? Ответ очевиден: исполнителем является компьютер. Точнее говоря, исполнителем является комплекс ЭВМ + Система программирования (СП). Программист составляет программу на том языке, на который ориентирована СП. Иногда в литературе такой комплекс называют виртуальной ЭВМ. Например, компьютер с работающей системой программирования на Бэйсике называют Бэйсик-машиной; компьютер с работающей системой программирования на Паскале называют Паскаль-машиной и т.п. Схематически это изображено на рис. 2. Входным языком такого исполнителя является язык программирования Паскаль. Независимо от того, на каком языке программирования будет написана программа, алгоритм решения любой задачи на ЭВМ может быть составлен из команд:

• присваивания;
• ввода;
• вывода;
• обращения к вспомогательному алгоритму;
• цикла;
• ветвления.

Источник