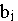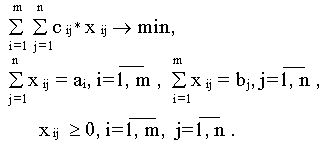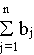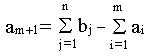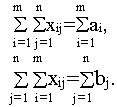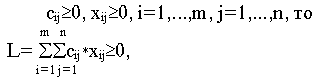Математические модели любых транспортных задач линейного программирования имеют общие черты

Введение

Наиболее развитыми в области решения оптимизационных задач являются методы линейного программирования. Эти методы позволяют описать с достаточной точностью широкий круг задач коммерческой деятельности, таких, как: планирование товарооборота; размещение розничной торговой сети города; планирование товароснабжения города, района; прикрепление торговых предприятий к поставщикам; организация рациональных перевозок товаров (транспортная задача); распределение работников торговли по должностям (задача о назначении); организация рациональных закупок продуктов питания (задача о диете); распределение ресурсов; планирование капиталовложений; оптимизация межотраслевых связей; замена торгового оборудования; определение оптимального ассортимента товаров в условиях ограниченной площади; установление рационального режима работы.

Если содержательный смысл требует получения решения в целых числах, то такая задача является задачей целочисленного профаммирования.

Общая задача линейного программирования: Постановка задачи коммерческой деятельности может быть представлена в виде математической модели линейного программирования, если целевая функция может быть представлена в виде линейной формы, а связь с ограниченными ресурсами описывается посредством линейных уравнений или неравенств. Кроме того, вводится дополнительное ограничение — значения переменных должны быть неотрицательны, поскольку они представляют такие величины, как товарооборот, время работы, затраты и другие экономические показатели.

Теоретическая основа линейного программирования

Основные понятия линейного программирования транспортной задачи

линейное программирование оптимизационная задача

Объектом изучения является решение задач линейного программирования. Транспортных задач. Построение первично опорного плана.

Классическая транспортная задача ЛП формулируется следующим образом.

Имеется m пунктов производства (поставщиков) и n пунктов

потребления (потребителей) однородного продукта. Заданы величины:

— объем производства (запас) i-го поставщика, i=1, m;

— объем потребления (спрос) j-го потребителя, i=1, n;

— стоимость перевозки (транспортные затраты) единицы продукта от i-го поставщика к j-му потребителю.

Требуется составить такой план перевозок, при котором спрос всех потребителей был бы выполнен, и при этом общая стоимость всех перевозок была бы минимальна.

Математическая модель транспортной задачи имеет вид:

Транспортная задача, в которой суммарные запасы и суммарные потребности

Совпадают, называется закрытой моделью; в противном случае — открытой. Открытая модель решается приведением к закрытой. В случае, когда суммарные запасы превышают суммарные потребности, т.е.

вводится фиктивный n+1 потребитель, потребности которого

В случае, когда суммарные потребности превышают суммарные запасы, т.е

вводится фиктивный m+1 поставщик, запасы которого

Стоимость перевозки единицы груза как до фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика полагают равными нулю, так как груз в обоих случаях не перевозится.

Прежде чем решать транспортную задачу, необходимо проверить, к какой модели она принадлежит, и если необходимо, то привести ее к закрытой модели.

Основные свойства транспортной задачи

Математические модели любых транспортных задач ЛП обладают общими чертами, а именно,

1) коэффициенты целевой функции неотрицательны (стоимости перевозок не могут быть отрицательными величинами);

2) коэффициенты правых частей ограничений неотрицательны (запасы и потребности продукта);

3) коэффициенты в ограничениях принимают только два значения, это нули и единицы.

В силу этих особенностей транспортная задача обладает следующими свойствами.

Теорема 1. Базисное решение закрытой модели транспортной задачи содержит m+n-1 базисных компонентов.

Доказательство. Количество базисных компонент определяется число линейно-независимых ограничений задачи. В транспортной задаче не все m+n ограничений линейно-независимы. Действительно, сложив первые m ограничений и следующие n ограничений задачи, получим

Но в закрытой модели выполняется балансовое равенство

поэтому получаем, что нетривиальная линейная комбинация строк ограничений (линейная комбинация с ненулевыми коэффициентами) равна нулю. Это означает, что среди ограничений задачи есть линейно-зависимое ограничение. Следовательно, число линейно-независимых ограничений равно m+n-1 и базис задачи состоит из m+n-1 компонент. Теорема доказана.

В силу специфики содержательной постановки транспортной задачи допустимое решение называется планом, базисное допустимое решение называется опорным планом, оптимальное решение называется оптимальным планом.

Теорема 2. Оптимальный план закрытой модели транспортной задачи существует всегда.

Доказательство. Оптимальное решение задачи ЛП существует, если, во-первых, существует допустимое решение и, во-вторых, целевая функция ограничена на этом допустимом решении.

Покажем существование допустимого решения. Так как суммарные запасы совпадают с суммарными потребностями то всегда можно найти такой план перевозок, который будет допустимым решением (все запасы вывозятся и все потребности выполняются в силу балансового равенства).

Покажем ограниченность целевой функции. Так как

Следовательно, L ограничена снизу нулем для всех допустимых решений. Теорема доказана.

Источник

Транспортная_задача

Классическая транспортная задача ЛП формулируется следующим образом.

Имеется m пунктов производства (поставщиков) и n пунктов

потребления (потребителей) однородного продукта. Заданы величины:

— объем производства (запас) i-го поставщика, i=1, m ;

— объем потребления (спрос) j-го потребителя, i=1, n ;

— стоимость перевозки (транспортные затраты) единицы продукта от i-го поставщика к j-му потребителю.

Требуется составить такой план перевозок, при котором спрос

всех потребителей был бы выполнен и при этом общая стоимость всех

перевозок была бы минимальна.

Математическая модель транспортной задачи имеет вид

Транспортная задача, в которой суммарные запасы

совпадают, называется закрытой моделью; в противном случае — открытой. Открытая модель решается приведением к закрытой.

В случае, когда суммарные запасы превышают суммарные

вводится фиктивный n+1 потребитель, потребности которого

В случае, когда суммарные потребности превышают суммарные

, вводится фиктивный m+1 поставщик, запасы которого

Стоимость перевозки единицы груза как до фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика

полагают равными нулю, так как груз в обоих случаях не перевозится.

Прежде чем решать транспортную задачу, необходимо проверить, к какой модели она принадлежит, и если необходимо, то привести ее к

9.2 Основные свойство транспортной задачи

Математические модели любых транспортных задач ЛП обладают общими чертами, а именно,

1) коэффициенты целевой функции неотрицательны (стоимости перевозок не могут быть отрицательными величинами);

2) коэффициенты правых частей ограничений неотрицательны (запасы и потребности продукта);

3) коэффициенты в ограничениях принимают только два значения, это нули и единицы.

В силу этих особенностей транспортная задача обладает следующими свойствами.

Базисное решение закрытой модели транспортной задачи содержит m+n-1 базисных компонент.

Количество базисных компонент определяется число линейно-независимых ограничений задачи. В транспортной задаче не все m+n ограничений линейно-независимы.

Действительно, сложив первые m ограничений и следующие n ограничений задачи, получим

Но в закрытой модели выполняется балансовое равенство

поэтому получаем, что нетривиальная линейная комбинация строк ограничений (линейная комбинация с ненулевыми коэффициентами) равна нулю. Это означает, что среди ограничений задачи есть линейно-зависимое ограничение. Следовательно, число линейно-независимых ограничений равно m+n-1 и базис задачи состоит из m+n-1 компонент.

В силу специфики содержательной постановки транспортной задачи допустимое решение называетсяпланом, базисное допустимое решение называется опорным планом, оптимальное решение называетсяоптимальным планом.

Оптимальный план закрытой модели транспортной задачи существует всегда.

Оптимальное решение задачи ЛП существует, если, во-первых, существует допустимое решение и, во-вторых, целевая функция ограничена на этом допустимом решении.

Покажем существование допустимого решения. Так как

совпадают с суммарными потребностями

то всегда можно найти такой план перевозок, который будет допустимым решением (все запасы вывозятся и все потребности выполняются в силу балансового равенства).

Покажем ограниченность целевой функции.

следовательно L ограничена снизу нулем для всех допустимых решений.

Источник

Транспортная задача. Математическая модель [ч.1]

Решение:
1. Вводим переменные задачи (матрицу перевозок):

2. Записываем матрицу стоимостей:

3. Целевая функция задачи равняется сумме произведений всех соответствующих элементов матриц C и X.

Данная функция, определяющая суммарные затраты на все перевозки, должна достигать минимального значения.

4. Составим систему ограничений задачи.
Сумма всех перевозок, стоящих в первой строке матрицы X, должна равняться запасам первого поставщика, а сумма перевозок во второй строке матрицы X равняться запасам второго поставщика:

Это означает, что запасы поставщиков вывозятся полностью.

Суммы перевозок, стоящих в каждом столбце матрицы X, должны быть равны запросам соответствующих потребителей:

Это означает, что запросы потребителей удовлетворяются полностью.

Необходимо также учитывать, что перевозки не могут быть отрицательными:

Ответ: Таким образом, математическая модель рассматриваемой задачи записывается следующим образом:
Найти переменные задачи, обеспечивающие минимум целевой функции (1) и удовлетворяющие системе ограничений (2) и условиям неотрицательности (3).

Источник