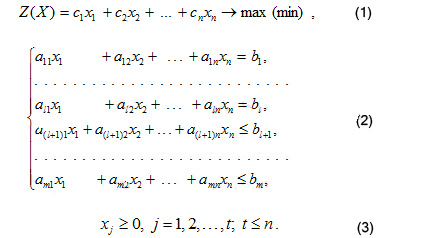Математические модели экономических задач линейного программирования

Математические модели задач линейного программирования

Переменными задачи называются величины Х1, Х2, Хn, которые полностью характеризуют экономический процесс. Обычно их записывают в виде вектора: X=(X₁, X₂. X_n).

Системой ограничений задачи называют совокупность уравнений и неравенств, описывающих ограниченность ресурсов в рассматриваемой задаче.

Целевой функцией задачи называют функцию переменных задачи, которая характеризует качество выполнения задачи и экстремум которой требуется найти.

В общем случае задача линейного программирования может быть записана в таком виде:

Данная запись означает следующее: найти экстремум целевой функции (1) и соответствующие ему переменные X=(X₁, X₂. X_n) при условии, что эти переменные удовлетворяют системе ограничений (2) и условиям неотрицательности (3).

Допустимым решением (планом) задачи линейного программирования называется любой n-мерный вектор X=(X₁, X₂. X_n), удовлетворяющий системе ограничений и условиям неотрицательности.

Множество допустимых решений (планов) задачи образует область допустимых решений (ОДР).

Оптимальным решением (планом) задачи линейного программирования называется такое допустимое решение (план) задачи, при котором целевая функция достигает экстремума.

Пример составления математической модели

Задача использования ресурсов (сырья)

Условие: Для изготовления n видов продукции используется m видов ресурсов. Составить математическую модель.

• b_i ( i = 1,2,3. m) — запасы каждого i-го вида ресурса;
• a_ij ( i = 1,2,3. m; j=1,2,3. n) — затраты каждого i-го вида ресурса на производство единицы объема j-го вида продукции;
• c_j ( j = 1,2,3. n) — прибыль от реализации единицы объема j-го вида продукции.

Требуется составить план производства продукции, который обеспечивает максимум прибыли при заданных ограничениях на ресурсы (сырье).

Введем вектор переменных X=(X₁, X₂. X_n), где x_j ( j = 1,2. n) — объем производства j-го вида продукции.

Затраты i-го вида ресурса на изготовление данного объема x_j продукции равны a_ijx_j, поэтому ограничение на использование ресурсов на производство всех видов продукции имеет вид:
Прибыль от реализации j-го вида продукции равна c_jx_j , поэтому целевая функция равна:

Ответ — Математическая модель имеет вид:

Источник

20. Задачи линейного программирования, экономическая модель

Переменных, уравнений, неравенств, их системы, функции.

В рамках линейного программирования рассматривается только линейные модели, т. е. все переменные в управлениях, переменных и функций в 1-ой степени. Способ решения задач представлен в виде алгоритма, должна быть возможность перенести решение задачи на компьютер (ЭВМ).

Основные экономические задачи линейного программирования

Экономическая модель задачи

Для построения экономической модели задач необходимы следующие допущения:

Пусть некоторая организация решает задачу о состоянии плана производства, которая решает некоторые производственные программы в течении некоторого промежутка времени.

• Количество ресурсов, которое она может использовать в течении рассматриваемого пространства времени
• Количество видов продукции, которые она должна выпускать

Обычно известен минимум выпускаемой продукции по каждому виду.

Для выполнения плана производства организация использует некоторые технологии. Под технологиями будем понимать – количественный перечень ресурсов и видов готовой продукции.

Для отражения связей между количеством использованных ресурсов и количеством готовой продукции, используется предпосылка линейности:

• Для каждой технологии затраты ресурсов и видов готовой продукции пропорциональны интенсивности ее применения
• Организации известны цены на единицы готовой продукции по каждому виду.
• Руководствуя, ценами организация заинтересована в таком состоянии расходов ресурсов и выпуска готовой продукции, чтобы обеспечить наибольшую прибыль.

План производства – перечень технологий с указанием интенсивности их применения.

Допустимый (возможный) план производства – план, обеспечивающий выполнение задания по производству и не противоречий лимиту ресурсов.

Критерии выбора плана это цель, которой подчинено производство.

Оптимальный план – это, допустимый план производства наилучший по выбранному критерию.

21. Основы мат. Моделирования, мат. Модель задачи линейного программирования

Математической моделью задачи называется совокупность математических соотношений, описывающих суть задачи.

Составление математической модели включает:

• выбор переменных задачи
• составление системы ограничений
• выбор целевой функции

Переменными задачи называются величины Х1, Х2, Хn, которые полностью характеризуют экономический процесс. Обычно их записывают в виде вектора: X=(X1, X2. Xn).

Системой ограничений задачи называют совокупность уравнений и неравенств, описывающих ограниченность ресурсов в рассматриваемой задаче.

Целевой функцией задачи называют функцию переменных задачи, которая характеризует качество выполнения задачи и экстремум которой требуется найти.

В общем случае задача линейного программирования может быть записана в таком виде:

Данная запись означает следующее: найти экстремум целевой функции (1) и соответствующие ему переменные X=(X1, X2. Xn) при условии, что эти переменные удовлетворяют системе ограничений (2) и условиям неотрицательности (3).

Допустимым решением (планом) задачи линейного программирования называется любой n-мерный вектор X=(X1, X2. Xn), удовлетворяющий системе ограничений и условиям неотрицательности.

Множество допустимых решений (планов) задачи образует область допустимых решений (ОДР).

Оптимальным решением (планом) задачи линейного программирования называется такое допустимое решение (план) задачи, при котором целевая функция достигает экстремума.

Источник

1.6. Общая экономико-математическая модель задачи линейного программирования

Общая линейная экономико-математическая модель экономических процессов и явлений — так называемая общая задача линейного программирования подается в виде:

(1)

(2)

(3.3)

Где нужно найти значение переменных x₁, x₂, …, x_n, которые удовлетворяют условиям (2) и (3), и целевая функция (1) приобретает экстремальный (максимальное или минимальное) значение.

Для общей задачи линейного программирования используются такие понятия.

Вектор Х = (х₁, х₂, …, х_n), координаты которого удовлетворяют системе ограничений (2) и условия неотрицательности переменных (3), называется допустимым решением (планом) задачи линейного программирования.

Допустимый план Х = (х₁, х₂, …, х_n) называется опорным планом задачи линейного программирования, если он удовлетворяет не менее, чем m линейно независимых ограничений системы (2) в виде равенств, а также ограничению (3) относительно неотрицательности переменных.

Опорный план Х = (х₁, х₂, …, х_n), называется невырожденным, если он содержит точно m положительных переменных, иначе он вырожденный.

Опорный план , при котором целевая функция (1) достигает максимального ( минимального ли) значение, называетсяоптимальным решением (планом) задачи линейного программирования.

Задачу (1)—(3) можно легко свести к канонической форме, т.е. к такому виду, когда в системе ограничений (2) все b_i (i = 1, 2, …, m) неотрицательные, а все ограничения являются равенствами.

Если какое-то b_i отрицательное, то, умножив i-тое ограничение на (– 1), получим в правой части соответствующее положительное значение. Когда i—тое ограничение имеет вид неравенства а_i1х₁+а_i2х₂+…+а_inx_n ≤ b_i, то последнюю всегда можно свести к равенству, введя дополнительную переменную x_n+1:

Аналогично ограничение вида а_k1x₁ + a_k2x₂ + … + a_knx_n ≥ b_k сводят к равенству, вычитая из левой части дополнительную переменную х_n+2, т.е.:

7. Геометрическая интерпретация задачи линейного программирования

Рассмотрим на плоскости х₁Оx₂ совместную систему линейных неравенств:

(1)

Каждое неравенство этой системы геометрически определяет полуплоскость с предельной прямой a_i1x₁ + a_i2x₂ = b_i (i=1,2, . т). Условия неотрицательности переменных определяют полуплоскости с предельными прямыми х₁ = 0 и х₂ = 0. Система совместная, поэтому полуплоскости как выпуклые множества, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты каждой из которых является решением данной системы (рис.1.1).

Совокупность этих точек (решений) называют многоугольником решений, или областью допустимых планов (решений) задачи линейного программирования. Это может быть точка (единое решение), отрезок, луч, многоугольник, неограниченная многоугольная область.

Если в системе ограничений (1) будет три переменных, то каждая неравенство геометрически будет определять полупространство трехмерного просторнства, предельными плоскостями которого будут a_i1x₁ + a_i2x₂ + a_i3x₃ = b_i (i = 1, 2, . т), а условия неотрицательности – полупространства с предельными плоскостями х_j=0 (j = 1, 2, 3), где и – номер ограничения, а j–— номер переменной. Если система ограничений совместная, то эти полупространства как выпуклые множества, пересекаясь, образуют в трехмерном пространстве общую часть, которая называется многогранником решений. Он может быть точкой, отрезком, лучом, многоугольником, многогранником, многогранной неограниченной областью.

Пусть в системе ограничений (1) количество переменных больше, чем три: х₁, х₂,…х_n; тогда каждая неравенство определяет полупространство n-мерного пространства с предельной гиперплоскостью а_i1x₁ + a_i2x₂ + a_i3x₃ + … +a_inx_n = b_i (i = 1, 2, . т). Каждому ограничению вида (1) отвечают гиперплоскость и полупространство, которое лежит с одного стороны этой гиперплоскости, а условия неотрицательности — полупространства с предельными гиперплоскостями х_j = 0 (j=1, 2, 3, . n).

Если система ограничений совместная, то по аналогии с трехмерным пространством она образует общую часть в n-мерном пространстве — выпуклый многогранник допустимых решений.

Итак, геометрически задача линейного программирования представляет собой отыскание координат такой точки многогранника решений, при подстановке которых в целевую линейную функцию последняя достигает максимального (минимального) значения, причем допустимыми решениями являются все точки многогранника решений.

в п—мерном пространстве основных переменных можно геометрически интерпретировать как семью параллельных гиперплоскостей, положение каждой из которых определяется значением параметра Z.

Рассмотрим геометрическую интерпретацию задачи линейного программирования на примере. Пусть фермер принял решение выращивать озимую пшеницу и сахарнаю свеклу на площади 20 га, отведя под сахарную свеклу не меньше, чем 5 га. Технико-экономические показатели выращивания этих культур указаны в табл.1.1:

Таблица 1.1 — Показатели выращивания сельскохозяйственных культур

Источник