Машинное обучение python прогнозирование

Python AI: как построить нейронную сеть и делать прогнозы

Проще говоря, цель использования ИИ — заставить компьютеры думать так же, как люди. Это может показаться чем-то новым, но эта область родилась в 1950-х годах.

Представьте, что вам нужно написать программу на Python, которая использует ИИ для решения задачи судоку . Способ добиться этого — написать условные операторы и проверить ограничения, чтобы увидеть, можно ли разместить число в каждой позиции. Ну, этот Python-скрипт уже является приложением ИИ, потому что вы запрограммировали компьютер для решения проблемы!

Машинное обучение (ML) и глубокое обучение (DL) также являются подходами к решению проблем. Разница между этими методами и скриптом Python заключается в том, что ML и DL используют обучающие данные вместо жестко запрограммированных правил, но все они могут использоваться для решения задач с использованием ИИ. В следующих разделах вы узнаете больше о том, что отличает эти два метода.

Машинное обучение

Машинное обучение — это метод, при котором вы обучаете систему решать проблему вместо того, чтобы явно программировать правила. Возвращаясь к примеру с судоку в предыдущем разделе, чтобы решить проблему с помощью машинного обучения, вы должны собрать данные из решенных игр-судоку и обучить статистическую модель . Статистические модели — это математически формализованные способы аппроксимации поведения явления.

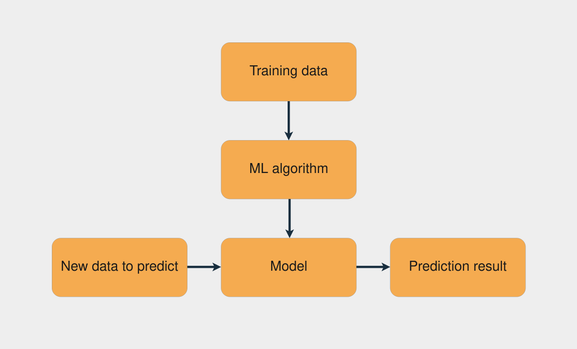
Распространенной задачей машинного обучения является обучение с учителем, в котором у вас есть набор данных с входными и известными выходными данными. Задача состоит в том, чтобы использовать этот набор данных для обучения модели, которая предсказывает правильные выходные данные на основе входных данных. На изображении ниже представлен рабочий процесс обучения модели с помощью обучения с учителем:

Комбинация обучающих данных с алгоритмом машинного обучения создает модель. Затем с помощью этой модели вы можете делать прогнозы для новых данных.

Примечание. scikit-learn — это популярная библиотека машинного обучения Python, которая предоставляет множество алгоритмов обучения с учителем и без учителя. Чтобы узнать больше об этом, ознакомьтесь с Разделение набора данных с помощью train_test_split() от scikit-learn .

Цель задач контролируемого обучения — делать прогнозы для новых, невидимых данных. Для этого вы предполагаете, что эти невидимые данные следуют распределению вероятностей, аналогичному распределению обучающего набора данных. Если в будущем это распределение изменится, вам нужно снова обучить свою модель, используя новый набор обучающих данных.

Разработка функций

Проблемы прогнозирования усложняются, когда вы используете в качестве входных данных различные типы данных. Проблема судоку относительно проста, потому что вы имеете дело непосредственно с числами. Что, если вы хотите научить модель предсказывать настроение в предложении? Или что, если у вас есть изображение, и вы хотите знать, изображен ли на нем кот?

Другое название входных данных — функция , а проектирование функций — это процесс извлечения функций из необработанных данных. При работе с различными видами данных вам необходимо найти способы представления этих данных, чтобы извлечь из них значимую информацию.

Примером техники разработки признаков является лемматизация , при которой вы удаляете склонение слов в предложении. Например, флективные формы глагола «смотреть», такие как «часы», «наблюдать» и «наблюдать», будут сокращены до их леммы или базовой формы: «смотреть».

Если вы используете массивы для хранения каждого слова корпуса, то применяя лемматизацию, вы получаете менее разреженную матрицу. Это может повысить производительность некоторых алгоритмов машинного обучения. На следующем изображении представлен процесс лемматизации и представления с использованием модели мешка слов :

Во-первых, флективная форма каждого слова сводится к его лемме. Затем подсчитывается количество вхождений этого слова. Результатом является массив, содержащий количество вхождений каждого слова в тексте.

Глубокое обучение

Глубокое обучение — это метод, в котором вы позволяете нейронной сети самостоятельно определять, какие функции важны, вместо того, чтобы применять методы проектирования функций. Это означает, что с помощью глубокого обучения вы можете обойти процесс разработки функций.

Отсутствие необходимости иметь дело с разработкой признаков — это хорошо, потому что процесс усложняется по мере того, как наборы данных становятся более сложными. Например, как бы вы извлекли данные, чтобы предсказать настроение человека по изображению его лица? С нейронными сетями вам не нужно об этом беспокоиться, потому что сети могут сами изучать функции. В следующих разделах вы углубитесь в нейронные сети, чтобы лучше понять, как они работают.

Нейронные сети: основные понятия

Нейронная сеть — это система, которая учится делать прогнозы, выполняя следующие шаги:

1. Получение входных данных
2. Делаем прогноз
3. Сравнение прогноза с желаемым результатом
4. Настройка его внутреннего состояния для правильного прогнозирования в следующий раз

Векторы , слои и линейная регрессия — вот некоторые из строительных блоков нейронных сетей. Данные хранятся в виде векторов, а в Python вы храните эти векторы в массивах . Каждый уровень преобразует данные, поступающие с предыдущего уровня. Вы можете думать о каждом слое как о шаге разработки признаков, потому что каждый слой извлекает некоторое представление данных, которые были получены ранее.

Одна интересная вещь о слоях нейронной сети заключается в том, что одни и те же вычисления могут извлекать информацию из любых данных. Это означает, что не имеет значения, используете ли вы данные изображения или текстовые данные. Процесс извлечения значимой информации и обучения модели глубокого обучения одинаков для обоих сценариев.

На изображении ниже вы можете увидеть пример сетевой архитектуры с двумя уровнями:

Каждый уровень преобразует данные, полученные с предыдущего уровня, применяя некоторые математические операции.

Процесс обучения нейронной сети

Обучение нейронной сети похоже на процесс проб и ошибок. Представьте, что вы впервые играете в дартс. В своем первом броске вы пытаетесь попасть в центральную точку мишени. Обычно первый выстрел делается просто для того, чтобы понять, как высота и скорость вашей руки влияют на результат. Если вы видите, что дротик находится выше центральной точки, вы настраиваете руку, чтобы бросить его немного ниже, и так далее.

Вот шаги для попытки попасть в центр мишени для дартс:

Обратите внимание, что вы продолжаете оценивать ошибку, наблюдая, куда приземлился дротик (шаг 2). Вы продолжаете, пока, наконец, не попадете в центр мишени.

С нейронными сетями процесс очень похож: вы начинаете со случайных весов и векторов смещения , делаете прогноз, сравниваете его с желаемым результатом и корректируете векторы для более точного прогноза в следующий раз. Процесс продолжается до тех пор, пока разница между прогнозом и правильными целями не станет минимальной.

Знание того, когда остановить обучение и какую цель точности установить, является важным аспектом обучения нейронных сетей, в основном из -за сценариев переобучения и недообучения .

Векторы и веса

Работа с нейронными сетями состоит в выполнении операций с векторами. Вы представляете векторы как многомерные массивы. Векторы полезны в глубоком обучении в основном из-за одной конкретной операции: скалярного произведения . Скалярное произведение двух векторов говорит вам, насколько они похожи с точки зрения направления, и масштабируется по величине двух векторов.

Основными векторами внутри нейронной сети являются векторы весов и смещения. Грубо говоря, вы хотите, чтобы ваша нейронная сеть проверяла, похожи ли входные данные на другие входные данные, которые она уже видела. Если новые входные данные аналогичны ранее просмотренным входным данным, то и выходные данные будут аналогичными. Вот как вы получаете результат предсказания.

Модель линейной регрессии

Регрессия используется, когда вам нужно оценить взаимосвязь между зависимой переменной и двумя или более независимыми переменными . Линейная регрессия — это метод, применяемый, когда вы аппроксимируете связь между переменными как линейную. Метод восходит к девятнадцатому веку и является самым популярным методом регрессии.

Примечание. Линейная связь — это связь, в которой существует прямая связь между независимой переменной и зависимой переменной.

Смоделировав взаимосвязь между переменными как линейную, вы можете выразить зависимую переменную как взвешенную сумму независимых переменных. Таким образом, каждая независимая переменная будет умножена на вектор с именем weight . Помимо весов и независимых переменных, вы также добавляете еще один вектор: смещение . Он устанавливает результат, когда все остальные независимые переменные равны нулю.

В качестве реального примера того, как построить модель линейной регрессии, представьте, что вы хотите обучить модель прогнозировать цену дома на основе площади и возраста дома. Вы решаете смоделировать эту связь с помощью линейной регрессии. Следующий блок кода показывает, как вы можете написать модель линейной регрессии для указанной проблемы в псевдокоде:

price = (weights_area * area) + (weights_age * age) + bias

В приведенном выше примере есть два веса: weights_area и weights_age . Процесс обучения состоит из корректировки весов и смещения, чтобы модель могла предсказать правильное значение цены. Для этого вам нужно вычислить ошибку прогноза и соответствующим образом обновить веса.

Это основы того, как работает механизм нейронной сети. Теперь пришло время посмотреть, как применять эти концепции с помощью Python.

Python AI: начинаем строить свою первую нейронную сеть

Первым шагом в построении нейронной сети является создание выходных данных из входных данных. Вы сделаете это, создав взвешенную сумму переменных. Первое, что вам нужно сделать, это представить входные данные с помощью Python и NumPy .

Обертывание входных данных нейронной сети с помощью NumPy

Вы будете использовать NumPy для представления входных векторов сети в виде массивов. Но прежде чем использовать NumPy, рекомендуется поиграть с векторами в чистом Python, чтобы лучше понять, что происходит.

В этом первом примере у вас есть входной вектор и два других весовых вектора. Цель состоит в том, чтобы найти, какой из весов больше похож на вход, принимая во внимание направление и величину. Вот как выглядят векторы, если вы их нарисуете:

weights_2 больше похож на входной вектор, поскольку он указывает в том же направлении, и величина также аналогична. Так как же определить, какие векторы похожи с помощью Python?

Во-первых, вы определяете три вектора, один для ввода и два других для весов. Затем вы вычисляете, насколько похожи input_vector и weights_1 . Для этого вы примените скалярное произведение . Поскольку все векторы являются двумерными векторами, вот шаги для этого:

1. Умножьте первый индекс input_vector на первый индекс weights_1 .
2. Умножьте второй индекс input_vector на второй индекс weights_2 .
3. Суммируйте результаты обоих умножений.

Вы можете использовать консоль IPython или блокнот Jupyter , чтобы следовать инструкциям. Хорошей практикой является создание новой виртуальной среды каждый раз, когда вы начинаете новый проект Python, поэтому вы должны сделать это в первую очередь. venv поставляется с Python версии 3.3 и выше и удобен для создания виртуальной среды.

Продолжение статьи будет позже.

Источник