Mann whitney test in python

Mann-Whitney U test (Wilcoxon rank sum test) in Python [pandas and SciPy]

If we have two independent groups with observations x₁, x₂, …, x_m and y₁, y₂, …, y_n sampled from X and Y populations, then Mann-Whitney U test compares each observation x_i from sample x with each observation (y_j) from sample y.

Null hypothesis: p (x_i > y_j ) = 0.5
Alternative hypothesis: p (x_i > y_j ) ≠ 0.5

Above two-sided alternative hypothesis tests that there is equal probability of x_i is greater or lesser than y_j (both groups came from same population),

One-sided alternative hypothesis tests probability of x_i is greater than y_j and vice versa.

We can also state the two-sided hypothesis in terms of median as (when two groups have same shape of distribution)

Null hypothesis: Two groups have equal median

Alternative hypothesis: Two groups does not have equal median

One-sided alternative hypothesis tests median from one group can be greater or lesser than other group.

Mann-Whitney U Test formula

The p value is calculated based on the comparison between the critical value and the U value. If U value null hypothesis and vice versa. If the sample is large (n>20), the p value is calculated based on the normal approximation using standardized test statistics.

How Mann-Whitney U Test works?

• Merge the data from two samples and rank them from smallest to largest
• Calculate the sum of rank for each sample (Rx and Ry)
• Calculate Mann-Whitney test statistic (U) using the formula (minimum of Ux and Uy)
• Calculate p value by comparing U with the critical value

Perform Mann-Whitney U test in Python

Mann-Whitney U test example

Suppose, there are two plant genotypes (A and B) differing in their yield phenotype. Mann-Whitney U test is appropriate to compare the yield of two genotypes under the assumption that yield output does not follow the normal distribution.

Get example dataset and summary statistics

Load hypothetical plant genotypes (A and B) yield dataset,

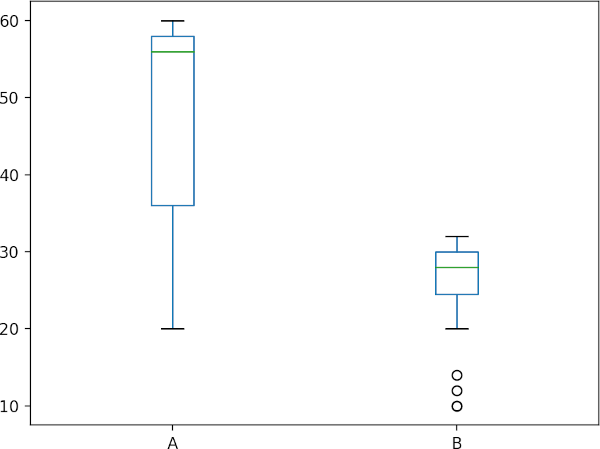
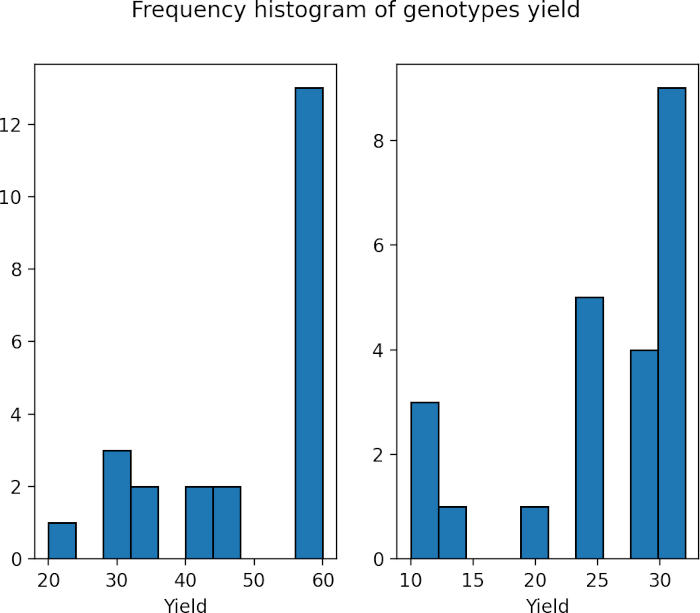
Check data distribution

Perform Mann-Whitney U test

Perform two-sided (yield of two genotypes does not have equal medians) Mann-Whitney U test,

Note: We are comparing median as two genotypes have similar shape of distribution (see histogram and boxplot). If two groups do not have similar shape of distribution, you should compare mean ranks.

   Check online calculator for performing Mann-Whitney U test

Note: In the above example, the p value obtained from mannwhitneyu is based on the normal approximation as the sample size is large (n > 20). If the sample size is small, a normal approximation is not appropriate. To get exact p value, set method=”exact”. The mannwhitneyu function automatically calculates the exact p value when one of the sample size is < 8. Both exact and normal approximation p values should be roughly similar.

Mann-Whitney U test interpretation: As the p value obtained from the Mann-Whitney U test is significant (U = 489.5, p < 0.05), we conclude that the yield of the two genotypes significantly different from each other .

Perform one-sided (median yield of A genotype is greater than median yield of genotype B) Mann-Whitney U test,

 As the p value obtained from the Mann-Whitney U test is significant (U = 489.5, p < 0.05), we conclude that the yield of the A genotype significantly greater than the genotype B.

Related reading

References

1. Nachar N. The Mann-Whitney U: A test for assessing whether two independent samples come from the same distribution. Tutorials in quantitative Methods for Psychology. 2008 Mar;4(1):13-20.
2. Mann–Whitney Test
3. Mann Whitney U Test (Wilcoxon Rank Sum Test)

If you have any questions, comments or recommendations, please email me at reneshbe@gmail.com

If you enhanced your knowledge and practical skills from this article, consider supporting me on

Updated: November 7, 2021

Share on

You may also enjoy

Two-Way ANOVA in R: How to Analyze and Interpret Results

Renesh Bedre 2 minute read

This article explains how to perform two-way ANOVA in R

How to Perform One-Way ANOVA in R (With Example Dataset)

Renesh Bedre 1 minute read

This article explains how to perform one-way ANOVA in R

What is Nextflow and How to Use it?

Renesh Bedre 1 minute read

Learn what is Nextflow and how to use it for running bioinformatics pipeline

How to Convert FASTQ to FASTA Format (With Example Dataset)

Renesh Bedre 1 minute read

List of Bioinformatics tools to convert FASTQ file into FASTA format

© 2023 Data science blog. Powered by Jekyll& Minimal Mistakes.

Источник

Как провести U-тест Манна-Уитни в Python

U- критерий Манна-Уитни используется для сравнения различий между двумя выборками, когда распределение выборки не является нормальным, а размеры выборки малы (n < 30).

В этом руководстве объясняется, как провести U-тест Манна-Уитни в Python.

Пример: U-тест Манна-Уитни в Python

Исследователи хотят знать, приводит ли обработка топлива к изменению среднего расхода топлива на галлон автомобиля. Чтобы проверить это, они измерили расход 12 автомобилей с обработкой топлива и 12 машин без нее.

Поскольку размеры выборки невелики, и исследователи подозревают, что распределение выборки не является нормальным, они решили выполнить U-критерий Манна-Уитни, чтобы определить, есть ли статистически значимая разница в милях на галлон между двумя группами.

Выполните следующие шаги, чтобы провести U-тест Манна-Уитни в Python.

Шаг 1: Создайте данные.

Во-первых, мы создадим два массива для хранения значений миль на галлон для каждой группы автомобилей:

group1 = [20, 23, 21, 25, 18, 17, 18, 24, 20, 24, 23, 19] **group2 = [24, 25, 21, 22, 23, 18, 17, 28, 24, 27, 21, 23] 

Шаг 2: Проведите U-тест Манна-Уитни.

Далее мы будем использовать функцию mannwhitneyu() из библиотеки scipy.stats для проведения U-теста Манна-Уитни, который использует следующий синтаксис:

mannwhitneyu(x, y, use_continuity=True, альтернатива=None)

• x: массив выборочных наблюдений из группы 1
• y: массив выборочных наблюдений из группы 2
• use_continuity: следует ли учитывать поправку на непрерывность (1/2). Значение по умолчанию — Истина.
• альтернатива: определяет альтернативную гипотезу. По умолчанию используется значение «Нет», которое вычисляет значение p, равное половине размера «двустороннего» значения p. Другие варианты включают «двусторонний», «меньше» и «больше».

Вот как использовать эту функцию в нашем конкретном примере:

import scipy.stats as stats #perform the Mann-Whitney U test stats. mannwhitneyu (group1, group2, alternative='two-sided') (statistic=50.0, pvalue=0.2114) 

Статистика теста равна 50,0 , а соответствующее двустороннее значение p равно 0,2114 .

Шаг 3: Интерпретируйте результаты.

В этом примере U-критерий Манна-Уитни использует следующие нулевую и альтернативную гипотезы:

H 0 : миль на галлон равны между двумя группами

H A : Расход топлива в милях на галлон для двух групп неодинаков .

Поскольку p-значение ( 0,2114 ) не меньше 0,05, мы не можем отвергнуть нулевую гипотезу.

Это означает, что у нас нет достаточных доказательств, чтобы сказать, что истинное среднее значение миль на галлон различается между двумя группами.

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнить U-критерий Манна-Уитни в различных статистических программах:

Источник

How to Conduct a Mann-Whitney U Test in Python

The Mann-Whitney U test, also known as the Wilcoxon rank-sum test, is a nonparametric statistical test that is used to determine if there are differences between two groups that are not normally distributed. This test can be used in lieu of the independent t-test when the assumptions of the t-test (i.e., normality and homogeneity of variance) are violated. The Mann-Whitney U test works by ranking all the values from both groups together and then evaluating whether each group has similarly high ranks.

Python’s scientific computing library, SciPy, includes the Mann-Whitney U test in its suite of statistical functions. This article will walk you through how to conduct a Mann-Whitney U test in Python using SciPy.

Hypothetical Scenario

For illustration, consider a hypothetical scenario: You are a researcher investigating a new medication designed to reduce the duration of common cold symptoms. You have a test group that has received the medication (Group A) and a control group that received a placebo (Group B). Both groups had the common cold, and you have recorded the duration (in days) of their cold symptoms.

The null hypothesis is that there is no difference between the median symptom duration for Group A and Group B. The alternative hypothesis is that there is a difference.

Performing the Mann-Whitney U Test

First, import the necessary Python libraries.

import numpy as np import pandas as pd from scipy.stats import mannwhitneyu

Next, let’s assume you have the symptom duration data stored in two Python lists:

groupA = [4.2, 3.8, 4.0, 4.3, 4.1, 4.0, 4.2] groupB = [5.2, 5.3, 5.0, 5.3, 5.1, 5.2, 5.3]

We can now perform the Mann-Whitney U test using the mannwhitneyu function from scipy.stats :

u_stat, p_value = mannwhitneyu(groupA, groupB, alternative='two-sided')

The mannwhitneyu function takes in two arguments – the two groups you want to compare. It returns the U statistic and the corresponding p-value. By default, the test is conducted as a one-tailed test, but by adding alternative='two-sided' , we conduct a two-tailed test.

Interpreting Results

Finally, we can print out the results:

print('U-statistic:', u_stat) print('P-value:', p_value)

The U statistic is the result of the Mann-Whitney U test calculation. This value by itself doesn’t tell us much, but the p-value is what we’re interested in.

The p-value is the probability of observing the data given that the null hypothesis is true. If the p-value is below our significance level (typically 0.05), we can reject the null hypothesis and infer that there is a significant difference in symptom duration between the two groups.

Conclusion

The Mann-Whitney U test is a powerful tool for statistical hypothesis testing when the assumptions of a t-test can’t be met. It provides a nonparametric alternative that can offer meaningful insights from your data.

One point to note is that while the Mann-Whitney U test determines whether two distributions are different, it does not tell us where the distributions differ or by how much they differ. Furthermore, like all tests, it does not ‘prove’ anything but merely provides evidence to support or refute a hypothesis. The strength of this evidence depends on the quality of your data and the appropriateness of the test for your specific situation.

Also, while the Python code snippets provided here serve to illustrate how one might conduct a Mann-Whitney U test, remember to conduct appropriate exploratory data analyses and check assumptions before conducting any statistical tests.

Python’s statistical and data handling capabilities, combined with good scientific practice, provide a robust framework for analyzing and drawing meaningful insights from your data, regardless of whether they adhere to the assumptions of parametric statistics.

Источник