1.5. Примеры задач линейного программирования
1.5. ПРИМЕРЫ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 17 Заметим, что в данной задаче на некоторые переменные может быть наложено требование целочисленности. 1.5.2. Задача о «смесях» Имеется n компонентов, при сочетании которых в различных пропорциях образуются различные смеси. В состав каждого компонента входят m веществ. Пусть a ij означает количество i -го вещества ( i = 1 , . . . , m ), которое входит в состав единицы j -го компонента ( j = 1 , . . . , n ), а a i — количество i -го вещества, которое входит в единицу смеси. Заданы числа c j ( j = 1 , . . . , n ), характеризующие цену единицы j -го компонента, и числа b i ( i = 1 , . . . , m ), указывающие минимально необходимое содержание i -го вещества в смеси. Требуется определить состав смеси минимальной стоимости. Пусть числа x j ( j = 1 , . . . , n ) характеризуют количество j -ой компоненты в смеси. Тогда задача принимает следующий вид. Требуется минимизировать функцию, характеризующую общую стоимость: n min å c j x j , j =1 при условиях обязательного минимального содержания каждого веще- ства: n å a ij x j ≥ b i ( i = 1 , . . . , m ) . j =1 По-видимому, одной из первых практических задач такого рода была задача составления диеты, поставленная и решенная в 1947 г. в США в Национальном бюро стандартов. Рассматриваемая система имела параметры m = 9, n = 77 (см. [ ? ], с. 521–527).
1.5.3. Транспортная задача
Пусть на m складах имеются различные количества некоторого товара, который необходимо доставить в n пунктов назначения. Точнее, i -ый склад распологает количеством товара, равным a i , тогда как j -ый пункт назначения должен получить b j единиц товара. Предполагается, что суммарный спрос равен суммарному предложению, т.е.
| m | n |
| å a i = å b j . | |
| i =1 | j =1 |
| 18 | ГЛАВА 1. ВВЕДЕНИЕ |
Кроме величин a i , b j заданы величины c ij , представляющие собой затраты на перевозку единицы груза от i -го слада до j -го пункта назначения. Требуется определить количества единиц товара x ij , подлежащих транспортировке от i -го склада в j -ый пункт назначения ( i = 1 , . . . , m ; j = 1 , . . . , n ;), чтобы при этом все запасы были исчерпаны, потребители удовлетворены и был достигнут минимум суммарных затрат. Таким образом, транспортная задача имеет следующий вид: m n min å å c ij x ij i =1 j =1
| n | ||||
| j m | = a i | |||
| å x ij | ( i = 1 , . . . , m ) , | |||
| å x | ij | = b | j | ( j = 1 , . . . , n ) , |
| =1 | ||||
| i =1 | ||||
| x ij ≥ 0 | ( i = 1 , . . . , m ; j = 1 , . . . , n ) . | |||
Раскроем встречающиеся суммы и обратим внимание на специальный вид матрицы ограничений: c 11 + . . . + c 1 n x 1 n + c 21 x 21 + . . . + c 2 n x 2 n + . . . + c m 1 x m 1 + . . . + c mn x mn )
| 11 | + | + x 1 | n | + x 21 + . . . + x 2 n | = a 2 | , | |||||||
| x | = a 1 | , | |||||||||||
| . . | . | . . . | . . . . . . | . . . | . . . . . . . . | . . . . . . | . . . . | . . . | . . | . . . | . . . . . . . . . . | . . . . . | . |
| + x | m 1 | + . . . + x mn = a m , | |||||||||||
| x | 11 | + x | + x | m 1 | = b | , | |||||||
| 21 | 1 | ||||||||||||
| x | + x | 22 | + x | m 2 | = b | , | |||||||
| 12 | 2 | ||||||||||||
| . . | . | . . . | . . . . . . | . . . . | . . . . . . . | . . . . . . | . . . . | . . . | . . . | . . | . . . . . . . . . . . | . . . . | . |
| x | 1 n | x | 2 n | x mn | = b n , | ||||||||
| x | ij | 0 ( i = 1 , . . . , m ; j = 1 , . . . , n ) . | |||||||||||
| ≥ | |||||||||||||
1.5.4. Задачи о назначениях
Рассмотрим задачу назначения n лиц на n работ в предположении, что эти лица различаются по своим способностям выполнять ту или иную работу, каждое лицо может быть назначено только на одну работу, каждая работа предназначается только для одного лица. Пусть с помощью опре- деленных тестов установлены величины c ij ( i = 1 , . . . , n ; j = 1 , . . . , n ), характеризующие «полезность» i -го лица на j -ой работе. Необходимо максимизировать суммарную полезность.
| 1.5. ПРИМЕРЫ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ | 19 | |
| Положим | ||
| x ij = | 1 если i -ое лицо назначается на j -ую работу, | |
| 0 , в противном случае. | (13) | |
Так как каждое лицо может быть назначено только на одну работу, то
| n | |||
| å x ij | = 1 | ( i = 1 , . . . , n ) . | (14) |
| j =1 | |||
| Так как каждая работа предназначается только для одного лица, то | |||
| n | |||
| å x ij | = 1 | ( j = 1 , . . . , n ) . | (15) |
| i =1 | |||
| Суммарная полезность выражается формулой: | |||
| n | n | ||
| å å c ij x ij . | (16) | ||
i =1 j =1 Итак, в математической постановке задача о назначениях заключается в максимизации функции ( 16 ), при ограничениях ( 13 – 15 ). В данной постановке задача о назначениях не является задачей линейного программирования. Этому препятствуют условия ( 13 ). Однако можно показать, что в данном случае условия ( 13 ) можно заменить условиями x ij ≥ 0 ( i = 1 , . . . , n ; j = 1 , . . . , n ) , сведя задачу о назначениях к частному случаю транспортной задачи. 1.5.5. Задача о «раскрое» Из некоторого материала требуется изготовить m различных изделий в количестве, пропорциональном числам b 1 , . . . , b m . Каждая единица материала может быть раскроена n различными способами, причем использование j -го способа дает a ij единиц i -го изделия. Найти план раскроя a единиц материала, обеспечивающий максимальное число комплектов изделий.
1 Методические указания по решению злп в среде Exсel
1.1 Максимизация прибыли предприятия Постановка задачи
Для выпуска 4 — х видов продукции требуется сырье, рабочее время и оборудование.
Для выпуска одной единицы продукции 1 — ого вида необходимо 3 ед. сырья, 22 ед. рабочего времени и 10 ед. оборудования.
Для выпуска одной единицы продукции 2 — ого вида необходимо 5 ед. сырья, 14 ед. рабочего времени и 14 ед. оборудования.
Для выпуска одной единицы продукции 3 — его вида необходимо 2 ед. сырья, 18 ед. рабочего времени и 8 ед. оборудования.
Для выпуска одной единицы продукции 4 — ого вида необходимо 4 ед. сырья, 30 ед. рабочего времени и 16 ед. оборудования.
Прибыль от продажи одной единицы продукции 1 — ого вида 30 руб., 2 — ого вида – 25 руб., 3 — его вида – 8 руб., 4 — ого вида – 16 руб.
Ресурсы ограниченны: имеется 60 ед. сырья, 400 ед. рабочего времени и 120 ед. оборудования.
А) Какое количество продукции каждого вида необходимо выпустить, чтобы максимизировать прибыль предприятия?
Б) Все ли продукты вошли в оптимальный план или существуют убыточные? На сколько нужно увеличить прибыль от продажи одной единицы убыточной продукции, чтобы она вошла в оптимальный план?
В) Каковы интервалы устойчивости для прибыли за одну единицу продукции каждого вида? Изменится ли оптимальное решение, если прибыли от продажи одной единицы продукции 4 – ого вида увеличить на 15 ед., 33 ед.? Уменьшить на 10 ед.?
Г) Какие ресурсы являются дефицитными? Как изменится оптимальное решение, если ресурс оборудование увеличить на 1 ед., уменьшить на 100 ед., 50 ед.?
Для удобства сведем данные задачи в следующую таблицу:
Нормы затрат ресурса на одну единицу продукции
Решение
I этап: Составление математической модели
- Переменные (неизвестные) задачи
Так как в задаче требуется определить количество продукции каждого вида, то введем следующие переменные: x1 – количество единиц продукции 1 — ого вида, x2 – количество единиц продукции 2 — ого вида, x3 – количество единиц продукции 3 — его вида, x4 – количество единиц продукции 4 — ого вида.
- Целевая функция
Т.к. цель задачи – максимизировать прибыль от продажи продукции (Р), то Р будет иметь вид: Р=30*x1+25*x2+8*x3+16*x4 (руб.) (*)
- Ограничения
Исходя из выражения для целевой функции, можно увидеть, что чем больше будут значения x1,x2,x3,x4, тем больше будет прибыль Р. Однако беспредельно увеличивать выпуск продукции невозможно, т.к. ресурсы предприятия ограничены, что приводит к ограничениям на x1,x2,x3,x4.3*x1+5*x2+2*x3+4*x4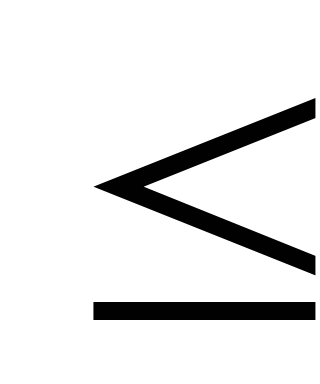
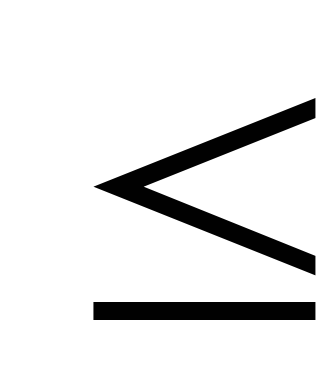
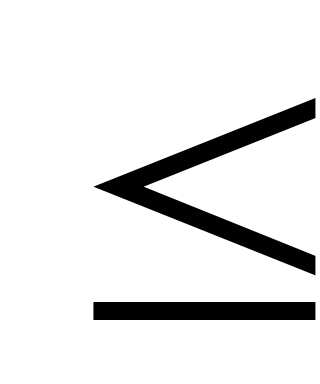
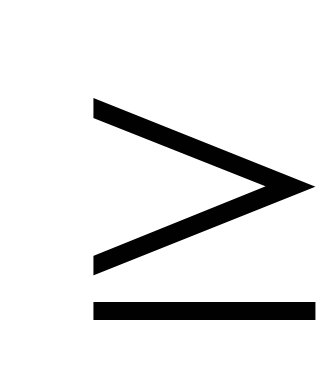
- В левой части i-ого i=1,2,3 функционального ограничения записано общее количество ресурса i-ого i=1,2,3 вида (сырья, рабочего времени и оборудования), необходимого для производства всей продукции.
- В ограничениях фигурирует знак “
”, т.к. количество ресурса, используемого для производства всей продукции, не должно превосходить запаса данного ресурса.
- Прямые ограничение (4) представляет собой следующее естественное условия: количество единиц выпускаемой продукции должно быть не отрицательным.
Таблица 2
| Неизвестные | |
| x1– количество единиц продукции 1 —ого вида, x2 – количество единиц продукции 2 —ого вида, x3– количество единиц продукции 3 — его вида, x4– количество единиц продукции 4 —ого вида. | |
| Целевая функция | Ограничения |
| Р=30*x1+25*x2+8*x3+16*x4 (руб.) | 3*x1+5*x2+2*x3+4*x4 60,22*x1+14*x2+18*x3+30*x4 60,22*x1+14*x2+18*x3+30*x4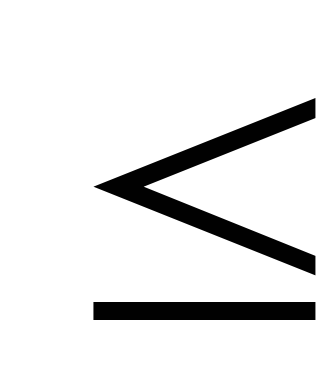 400,10*x1+14*x2+8*x3+16*x4 400,10*x1+14*x2+8*x3+16*x4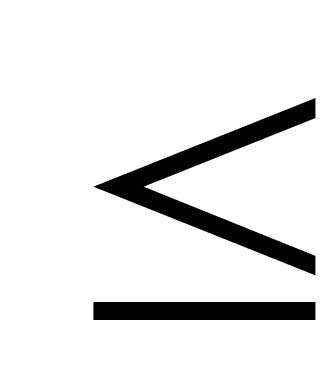 120,xi 120,xi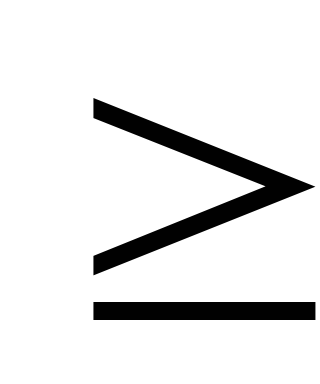 0, i=1,2,3,4 0, i=1,2,3,4 |
Для продолжения скачивания необходимо пройти капчу:
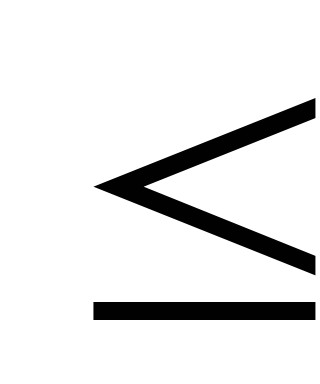 ”, т.к. количество ресурса, используемого для производства всей продукции, не должно превосходить запаса данного ресурса.
”, т.к. количество ресурса, используемого для производства всей продукции, не должно превосходить запаса данного ресурса.