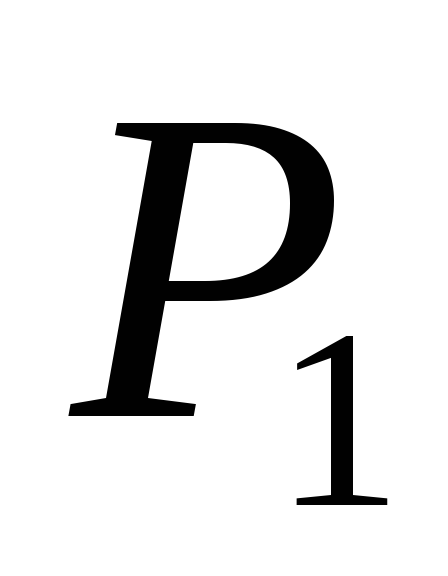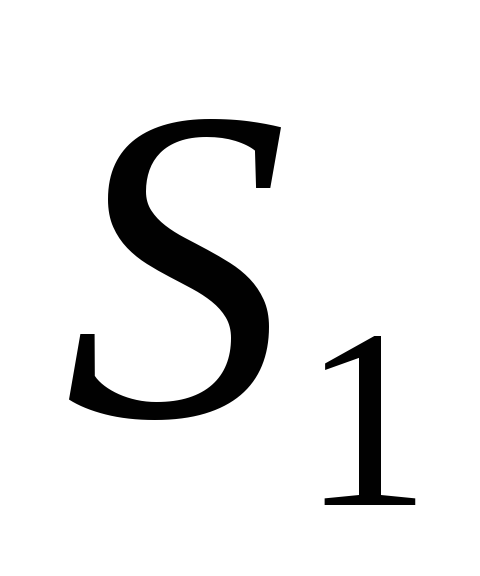Линейное программирование задача оптимального производства продукции

Тема 2.2. Линейное программирование

2.2.1. Моделирование задачи оптимизации производства методами линейного программирования.

Линейное программирование является одним из методов решения общих задач оптимизации, в которых учитывается большое число переменных, подчиненных определенным ограничениям. При решении этих задач необходимо получить оптимальное значение определенного критерия эффективности (функции цели), например прибылей, затрат, количества произведенных продуктов или других показателей, при условии, что удовлетворяются поставленные ограничения. Эти ограничения в свою очередь носят различный характер и объясняются условиями производства, управления, сбыта, хранения, наличием сырья или законодательными положениями.

Линейное программирование можно использовать для решения задач оптимизации, в которых выполняются следующие условия:

1. Необходимо наличие линейной функции цели, оптимальное значение которой необходимо отыскать. Требование линейности существенно для применения методов, изложенных в этой и следующей теме. Линейность означает, например, что для изготовления 10 изделий потребуется в10 раз больше средств, чем для получения одного изделия, или для получения 5 изделий уйдет в 5 раз больше времени, чем на изготовление одного изделия, и т.д. Если же такое допущение пропорциональной зависимости неверно или нельзя получить линейную функцию за счет преобразования переменных, то методы линейного программирования неприменимы.

2. Ограничения также должны быть заданы в виде системы линейных равенств или неравенств.

Если задача поставлена правильно, то можно использовать методы линейного программирования для ее решения.

Рассмотрим следующую производственную задачу:

Необходимо произвести два вида продукции в объемах х₁ и х₂, используя три ресурса, которые имеются в количестве b₁, b₂, b₃, соответственно. Известны нормативы потребления ресурсов на производство единицы первого и второго вида продукции:

a₁₁-количество первого ресурса, необходимого для производства единицы первого вида продукции;

a₁₂-количество первого ресурса, необходимого для производства единицы второго вида продукции;

a₂₁-количество второго ресурса, необходимого для производства единицы первого вида продукции;

a₂₂-количество второго ресурса, необходимого для производства единицы второго вида продукции;

a₃₁-количество третьего ресурса, необходимого для производства единицы первого вида продукции;

a₃₂-количество третьего ресурса, необходимого для производства единицы второго вида продукции.

Пусть c₁ и c₂ – прибыль от реализации единицы первого и второго вида продукции. Это постоянные факторы данной задачи.

Пример 2.2.1. Придадим постоянным факторам конкретные числовые значения и сведем их в табл.2.2.1.

Источник

Производственная задача линейного программирования

Построение математической модели следует начать с идентификации переменных (искомых величин). После этого определяются целевая функция и ограничения через соответствующие переменные.

В рассматриваемом примере имеем следующее:
Переменные.
Так как нужно определить объёмы производства каждого вида продукции, переменными являются:
X₁ — суточный объём производства изделия П₁в тыс. шт.;
Х₂ — суточный объём производства изделия П₂в тыс. шт.

Целевая функция. Так как стоимость 1 тыс. изделий П₁ равна 3 тыс. руб., суточный доход от её продажи составит 3Х₁тыс. руб. Аналогично доход от реализации Х₂ тыс. шт. П₂ составит 2Х₂ тыс. руб. в сутки. При допущении независимости объёмов сбыта каждого из изделий общий доход равен сумме двух слагаемых — дохода от продажи изделий П₁ и дохода от продажи изделий П₂.
Обозначив доход (в тыс. руб.) через f(X), можно дать следующую математическую формулировку целевой функции: определить (допустимые) значения X₁ и Х₂, максимизирующие величину общего дохода:
f(X) = 3X₁ + 2X₂, Х = (Х₁, Х₂)
Ограничения. При решении рассматриваемой задачи должны быть учтены ограничения на расход исходных продуктов А, В и С и спрос на изготовляемую продукцию, что можно записать так: Расход исходного продукта для производства обоих видов изделий
≤
Максимально возможный запас данного исходного продукта

Это приводит к трём ограничениям:
Х₁ + 2Х₂ ≤ 6 (для А),
2Х₁ + Х₂ ≤ 8 (для В),
Х₁ + 0.8Х₂ ≤ 5 (для С).
Ограничения на величину спроса на продукцию имеют вид:
Х₂ – X ₁ ≤ 1 (соотношение величин спроса на изделия П₁ и П₂),
Х₂ ≤ 2 (максимальная величина спроса на изделия П₂).
Вводятся также условия неотрицательности переменных, т.е. ограничения на их знак:
X ₁ ≥ 0 (объём производства П₁)
Х₂ ≥ 0 (объём производства П₂).
Эти ограничения заключаются в том, что объёмы производства продукции не могут принимать отрицательных значений.
Следовательно, математическая модель записывается следующим образом.
Определить суточные объёмы производства (X ₁ и Х₂) изделий П₁ и П₂ в тыс. шт., при которых достигается
max f(X) = 3 X ₁ + 2 X ₂ (целевая функция)
при ограничениях:
X₁ + 2Х₂ ≤ 6
2Х₁ + Х₂ ≤ 8
X₁ + 0.8Х₂≤
5 — X₁ + Х₂ ≤ 1
Х₂ ≤ 2
X₁ ≥0, Х₂≥ 0

Ресурсная задача

Для изготовления изделий типа А и В используется сырье трех видов, запасы каждого из которых Р1, Р2, Р3. На производство одного изделия типа А требуется затратить а1 кг сырья первого вида, а2 кг сырья второго вида, а3 кг сырья третьего вида. На одно изделие типа В расходуется соответственно b1, b2, b3 кг сырья каждого вида. Прибыль от реализации единицы изделия А составляет α ден.ед., а изделия В – β ден.ед. Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации. Решить задачу симплекс-методом. Дать геометрическое истолкование задачи.

Задача об использовании ресурсов (задача планирования производства)

Для изготовления двух видов продукции Р₁ и Р₂ используют три вида ресурсов S₁, S₂, S₃. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в табл. 1.

F = 2x₁ + 3x₂. (1)
Поскольку количество ресурсов, необходимых для производства продукции ограниченно, составим систему ограничений по ресурсам. Для изготовления продукции потребуется (2x₁ + 3x₂) единиц ресурса S₁, 3x₁ единиц ресурса S₂ и (x₁ + 4x₂) единиц ресурса S₃. Так как потребление ресурсов S₁, S₂, S₃ не должно превышать их запасов, 20, 18, 10 единиц, соответственно, то связь между потреблением ресурсов и их запасами выразится системой ограничений неравенств:

(2)
Итак, экономико-математическая модель задачи: найти такой план выпуска продукции , удовлетворяющий системе ограничений (2), при котором целевая функция (1) принимает максимальное значение.
Задачу об использовании ресурсов можно обобщить на случай выпуска n видов продукции с использованием m видов ресурсов.
Обозначим через x (j = 1, 2,…,n) – число единиц продукции P_j, запланированной к производству; b₁ (i = 1, 2,…,m) – запасы ресурсов S_i, a_ij – число единиц ресурса S_i, затрачиваемого на изготовление единицы продукции P_j; c_j – прибыль от реализации единицы продукции P_j. Тогда экономико-математическая модель задачи в общей постановке примет вид:

(4)
Найти такой план выпуска продукции, удовлетворяющий системе (4), при котором функция (3) принимает максимальное значение.
Замечание. Данную задачу называют ещё задачей определения оптимального ассортимента продукции.

Производственная задача на минимум

Бригада приняла заказ на изготовление 57 шт. продукции П1, 68 шт. продукции П2 и 80 шт. продукции П3. Продукция производится на станках А и В. Для изготовления на станке А единицы продукции П1 требуется 15 мин, единицы продукции П2 – 50 мин, единицы продукции П3 – 27 мин, на станке В – соответственно 11, 15 и 13 мин.

Постройте математическую модель задачи, на основании которой можно найти, сколько продукции и какого вида следует изготовить на станках А и В, чтобы заказ был выполнен в минимальное время.

Решение. Математическая модель задачи.
x₁ — изготовлено продукции П1 на станке A, шт.
x₂ — изготовлено продукции П1 на станке B, шт.
x₃ — изготовлено продукции П2 на станке A, шт.
x₄ — изготовлено продукции П2 на станке B, шт.
x₅ — изготовлено продукции П3 на станке A, шт.
x₆ — изготовлено продукции П3 на станке B, шт.

Задача оптимального производства продукции

1. Для производства двух видов продукции I и II с планом x₁ и x₂ единиц составить целевую функцию прибыли Z и соответствующую систему ограничений по запасам сырья, предполагая, что требуется изготовить в сумме не менее n единиц обоих видов продукции.
2. В условиях задачи 1 составить оптимальный план ( x₁, x₂) производства продукции, обеспечивающий максимальную прибыль Z_max. Определить остатки каждого вида сырья. (Задачу решить симплекс–методом)
3. Построить по полученной системе ограничений многоугольник допустимых решений и найти оптимальный план производства геометрическим путем. Определить соответствующую прибыль Z_max.

Источник

3.1.1. Задача планирования производства

Задача планирования производства (или задача об использовании ресурсов) является одной из разновидностей задачи линейного программирования.

Рассмотрим пример подобной задачи.

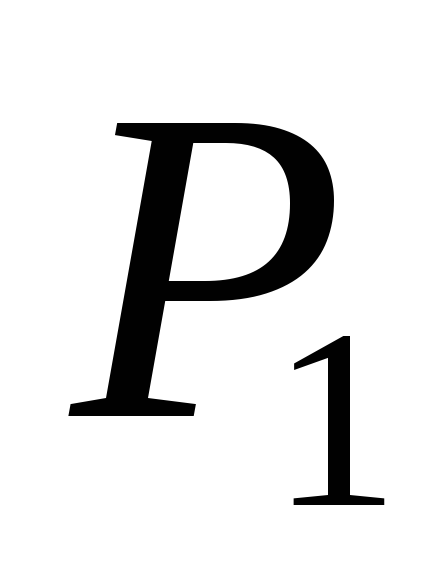
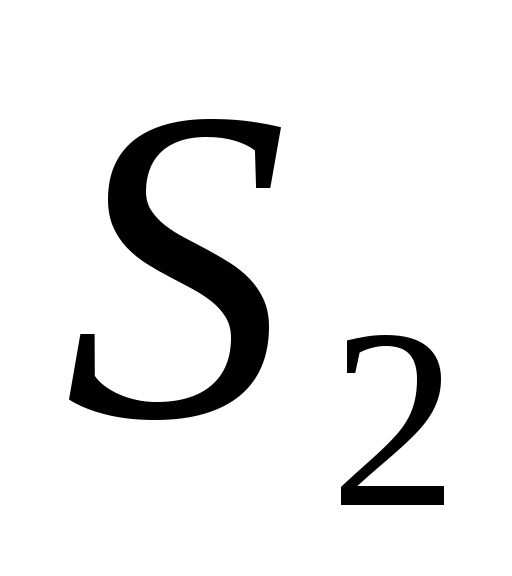
Для изготовления двух видов продукции ииспользуют четыре вида ресурсов,,и. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в табл.1 (цифры условные).

Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции

Число единиц ресурсов, затрачиваемых на изготовление единицы продукции

Прибыль, получаемая от единицы продукции и, – соответственно 2 и 3 руб.

Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной.

Решение. Составим экономико-математическую модель задачи.

Обозначим ,– число единиц продукции соответственнои, запланированных к производству. Для их изготовления потребуетсяединиц ресурса,единиц ресурса,единиц ресурсаиединиц ресурса. Так как потребление ресурсов,,ине должно превышать их запасов, соответственно 18, 16, 5 и 21 единицы, то связь между потреблением ресурсов и их запасами выразится системой неравенств:

(3.1.4)

По смыслу задачи переменные

(3.1.5)

Суммарная прибыль составитруб. от реализации продукцииируб.– от реализации продукции, т.е.

. (3.1.6)

Итак, экономико-математическая модель задачи: найти такой план выпуска продукции , удовлетворяющий системе (3.1.4) и условию (3.1.5), при котором функция (3.1.6) принимает максимальное значение.

Задачу легко обобщить на случай выпуска видов продукции с использованиемвидов ресурсов.

Обозначим – число единиц продукции, запланированной к производству;– запас ресурса,– число единиц ресурса, затрачиваемого на изготовление единицы продукции(числачасто называют технологическими коэффициентами);– прибыль от реализации единицы продукции.

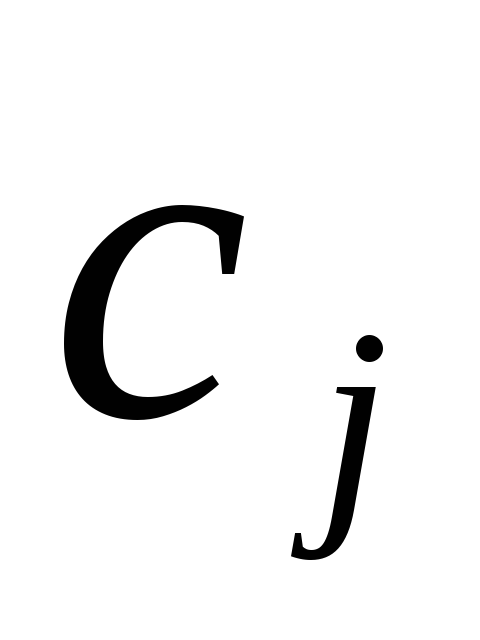
Тогда экономико-математическая модель задачи об использовании ресурсов в общей постановке примет вид: найти такой план выпуска продукции, удовлетворяющий системе

и условию при котором функцияпринимает максимальное значение.

Решение типового примера

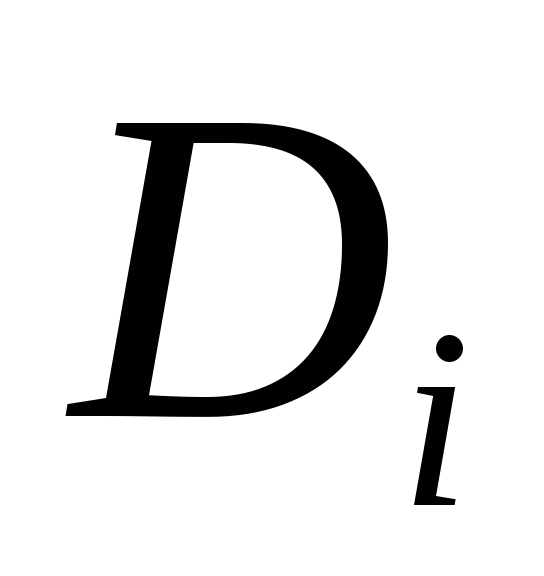
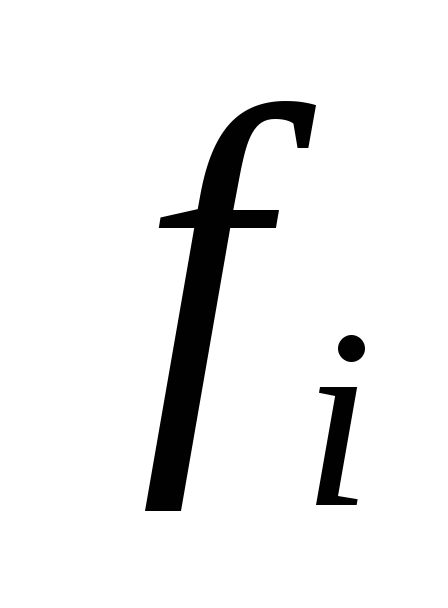
Предприятию ООО «ТИТАН», одним из видов деятельности которого является выполнение токарных, фрезерных и сверлильных работ, поступил заказ на производство гаек стремянки, гаек штанги, гаек МОД и колец шкворня в количестве соответственно шт. Производство заказанной токарной продукции в полном объеме ограничено запасами имеющихся ресурсов (трудозатратами –чел.-час., запасом стали –кг, а также выделенными денежными средствами на оплату труда рабочих и последующую обработку токарной продукции –руб.). Кроме того, известно, что для производства единицы продукции каждого вида требуется соответственнокг стали, трудозатраты при этом составляют соответственночел.-час. За каждую изготовленную деталь рабочий предприятия получаетруб., последующая обработка единицы изделия каждого вида требует затрат денежных средств в размереруб. соответственно.

Задача оптимизации производства для ООО «ТИТАН» ставится в форме максимизации дополнительной прибыли предприятия при заданных ассортименте выпускаемой продукции и ограничениях на имеющиеся запасы ресурсов, при условии, что прибыль от реализации единицы продукции каждого вида составляет соответственно руб.

Исходные данные задачи представлены в табл. 2.

Исходные данные задачи планирования производства

Ассортимент выпускаемой продукции

Источник