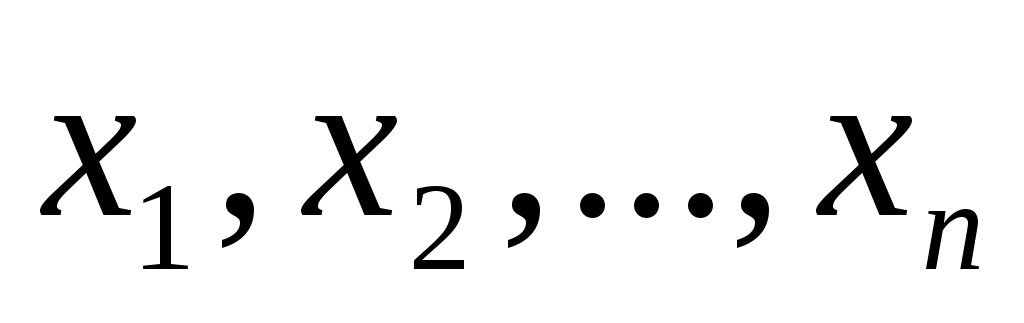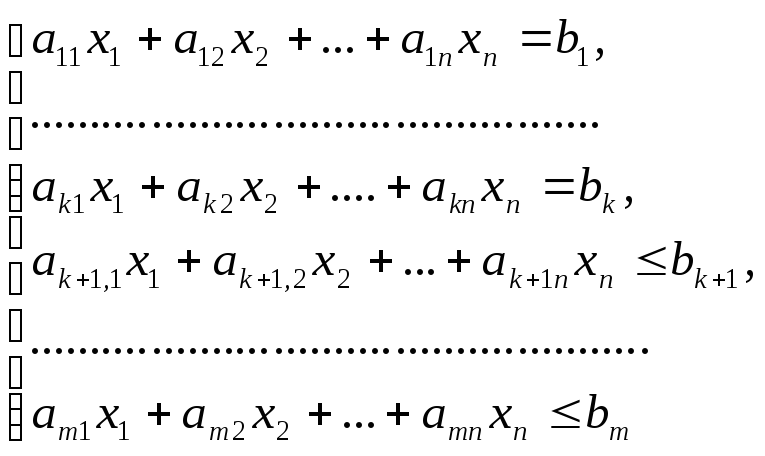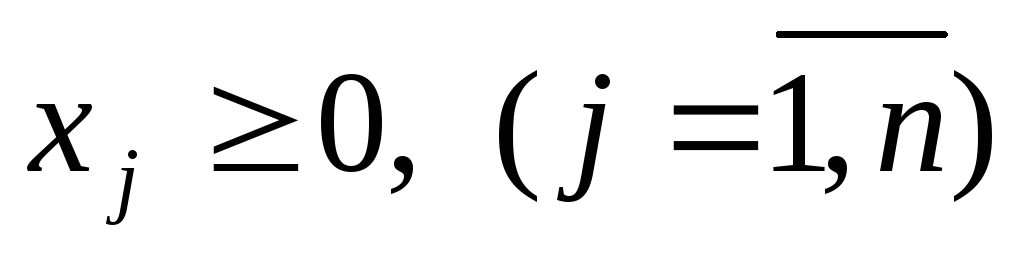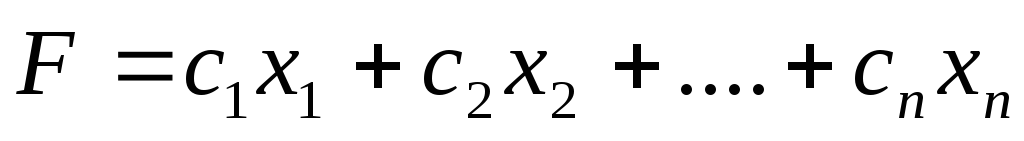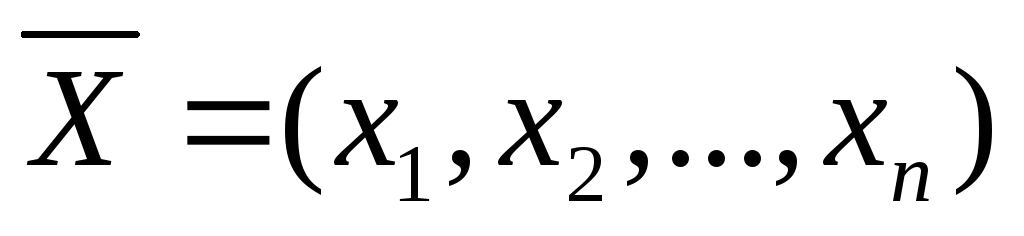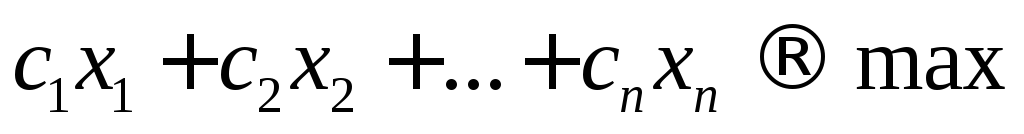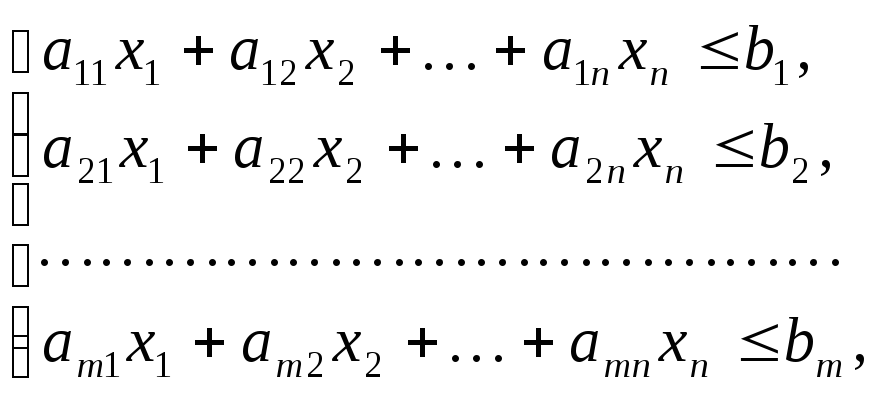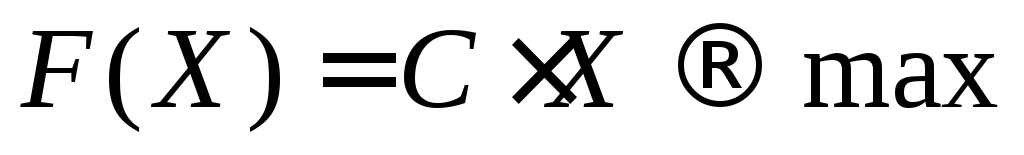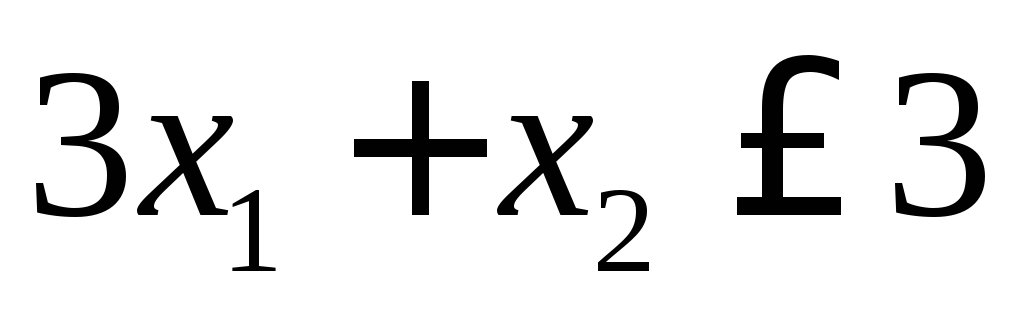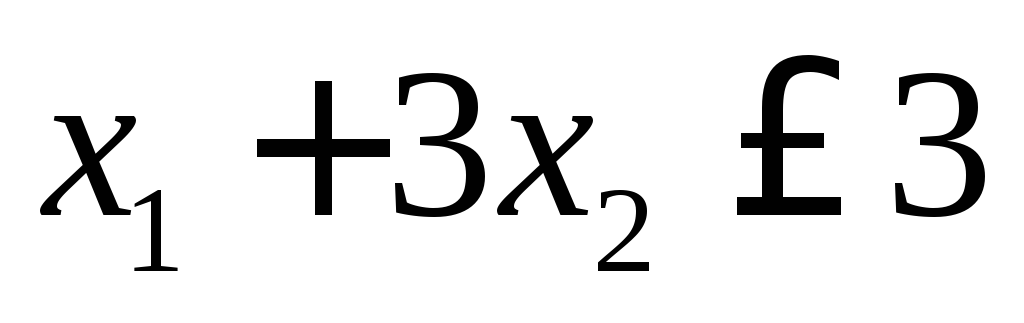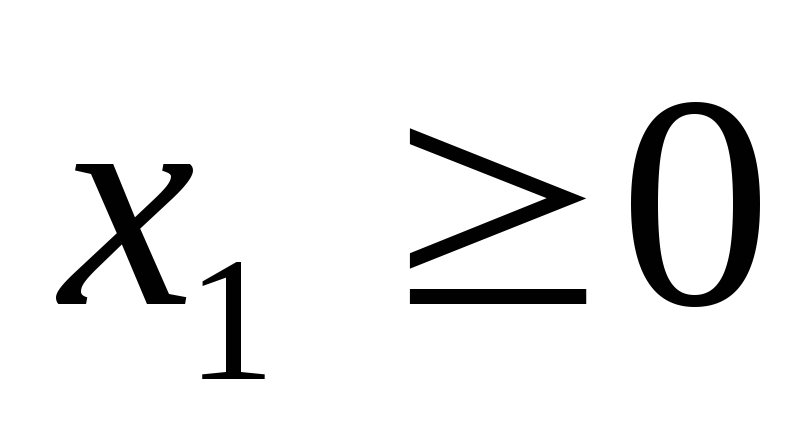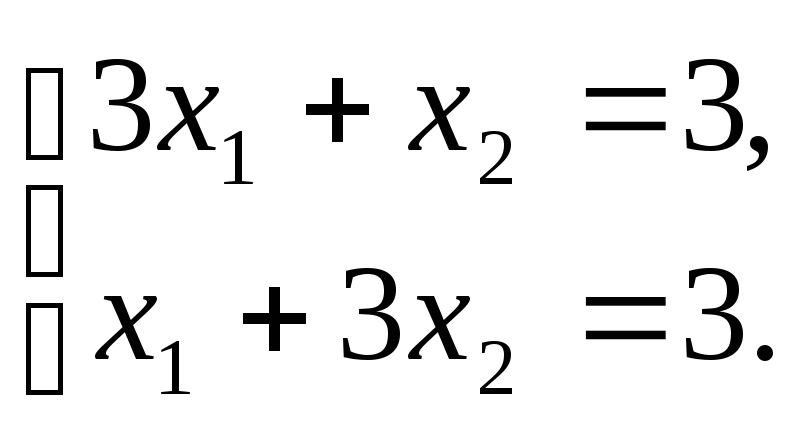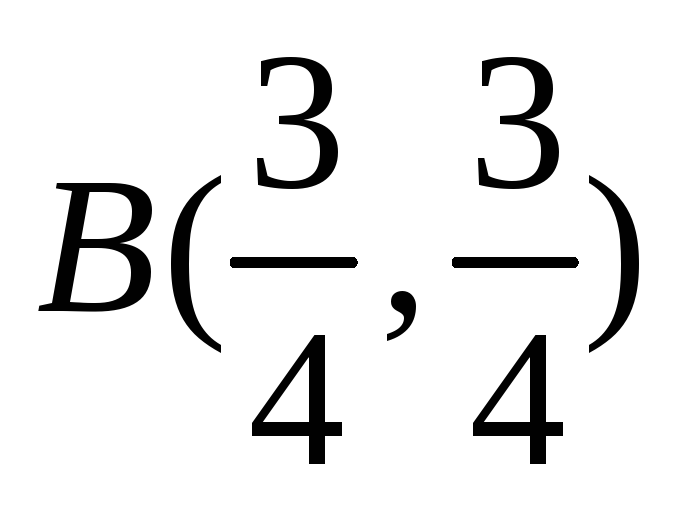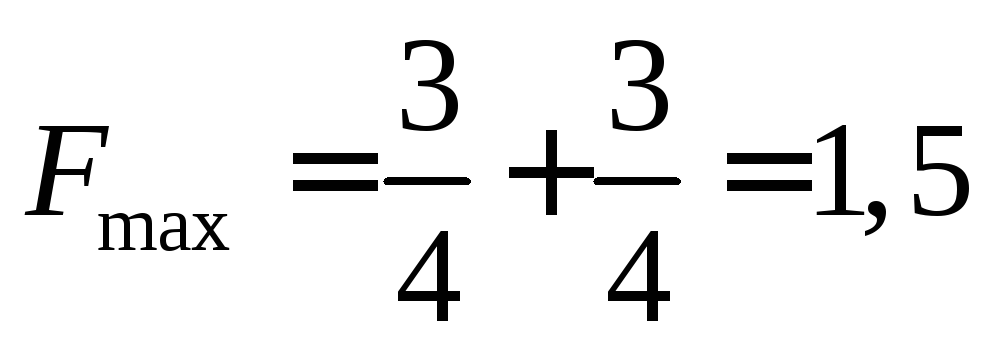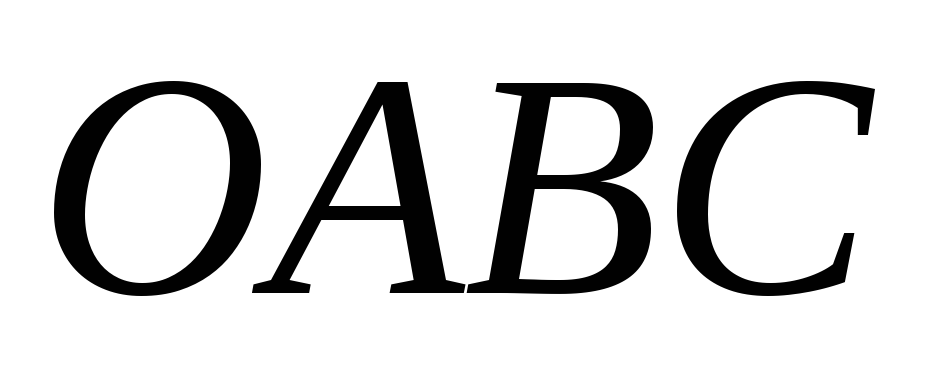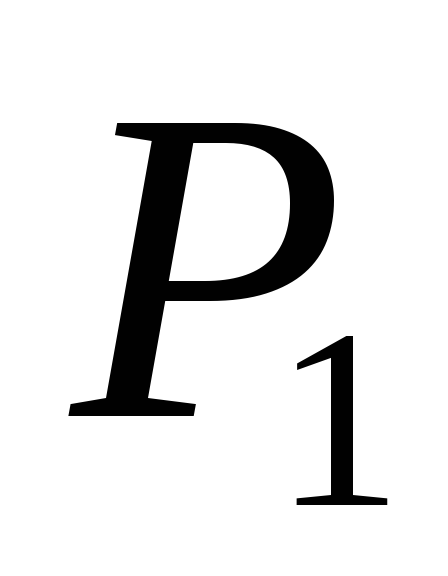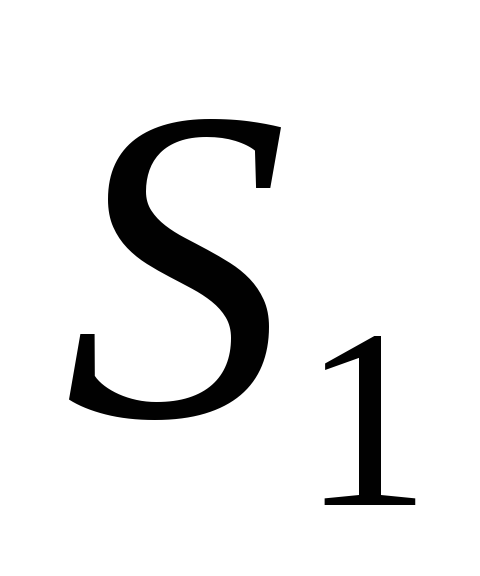Линейное программирование задача оптимального планирования производства

2. Задача об оптимальном использовании ресурсов при производственном планировании.

Общий смысл задач этого класса сводится к следующему.

Предприятие выпускает n различных изделий. Для их производства требуется m различных видов ресурсов (сырья, материалов, рабочего времени и т.п.). Ресурсы ограничены, их запасы в планируемый период составляют, соответственно, b₁, b₂. b_m условных единиц.

Известны также технологические коэффициенты a_ij, которые показывают, сколько единиц i-го ресурса требуется для производства единицы изделия j-го вида ( ).

Прибыль, получаемая предприятием при реализации изделия j-го вида, равна c_j.

В планируемом периоде значения величин a_ij, b_i и c_j остаются постоянными.

Требуется составить такой план выпуска продукции, при реализации которого прибыль преприятия была бы наибольшей.

Далее приведем простой пример задачи такого класса.

Компания специализируется на выпуске хоккейных клюшек и наборов шахмат. Каждая клюшка приносит компании прибыль в размере $2, а каждый шахматный набор — в размере $4. На изготовление одной клюшки требуется четыре часа работы на участке A и два часа работы на участке B. Шахматный набор изготавливается с затратами шести часов на участке A, шести часов на участке B и одного часа на участке C. Доступная производственная мощность участка A составляет 120 н-часов в день, участка В — 72 н-часа и участка С — 10 н-часов.

Сколько клюшек и шахматных наборов должна выпускать компания ежедневно, чтобы получать максимальную прибыль?

Условия задач указанного класса часто представляют в табличной форме (см. таблицу 2.1).

Таблица 2.1 — Исходные данные задачи об использовании производственных ресурсов

производственные участки

затраты времени на единицу продукции, н-час

доступный фонд времени, н-час

Источник

1.1 Линейное программирование как метод оптимального планирования

Линейное программирование (ЛП) изучает важную для практики задачу отыскания экстремума линейной функции при наличии ограничений в виде линейных неравенств или уравнений.

Сущность этих задач заключается в том, чтобы из множества различных вариантов исследуемого экономического процесса, выбрать по какому-либо признаку наилучший, или, как его называют, оптимальный вариант.

В этом методе обязателен специальный показатель выгодности плана, который называют показателем или критерием оптимального плана. Часто это прибыль, доход, валовый продукт, производительность, эффективность. В таких случаях выгодно, чтобы показатель оптимальности для выбранного плана был максимальным. Если показателем оптимальности плана служат издержки, себестоимость, капиталовложения или трудоемкость, то необходимо планировать так, чтобы показатель оптимальности для выбранного плана был минимальным.

Таким образом, ясно, что цель, которую мы ставим перед собой, заключается в максимизации или минимизации некоторого количества средств (денег, сырья, оборудования, продуктов питания), которое математически выражается в виде линейной формы некоторого числа переменных.

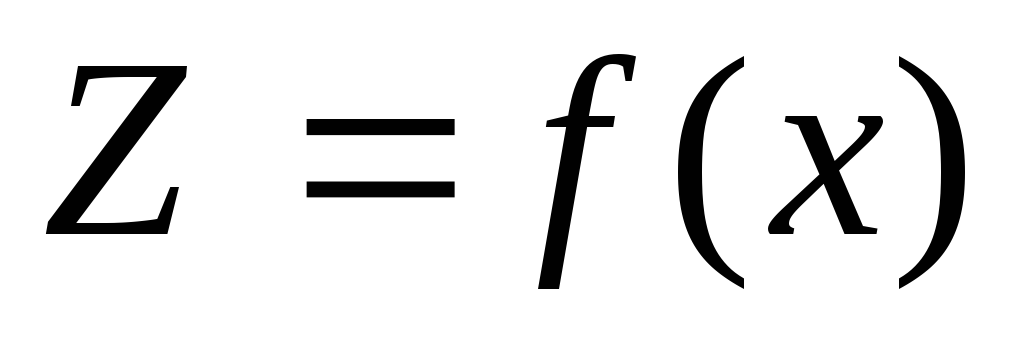
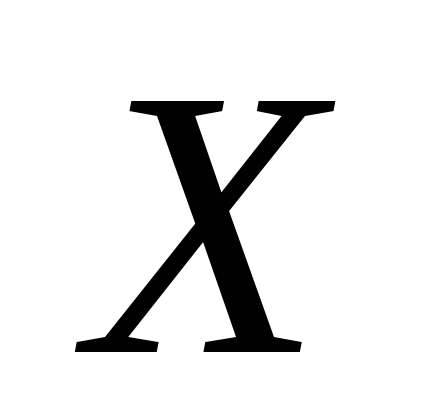
Множество возможных вариантов, из которых выбирается оптимальный план, всегда ограничено (ресурсами сырья, наличием рабочей силы, количеством оборудования и т. п.), поэтому каждый из рассматриваемых вариантов должен быть допустимым планом, удовлетворяющим имеющимся ограничениям. Показатель оптимальности плана является некоторой функцией плана. Поэтому задача отыскания оптимального плана сводится к математической задаче нахождения экстремума этой функции.

Решение экстремальных экономических задач можно разбить на 3 этапа: 1) построение экономико-математической модели; 2) нахождение оптимального решения одним из математических методов; 3) практическое внедрение.

Построение экономико-математической модели состоит в создании упрощенной экономической модели, в которой в схематической форме отражена сущность изучаемого процесса. При этом особое внимание должно быть уделено отражению в модели всех существенных особенностей задачи и учету всех ограничивающих условий, которые могут повлиять на результат. Затем определяют цель решения, выбирают критерий оптимальности и дают математическую формулировку задачи.

1.2 Общая задача линейного программирования

Общую задачу линейного программирования можно сформулировать следующим образом. Найти такие значения , которые удовлетворяют системе ограничений

(1.1)

(1.2)

и для которых линейная функция (целевая функция)

(1.3)

достигает экстремума (максимума или минимума).

Вектор , координаты которого удовлетворяют системе (1.1) и (1.2) называют опорным планом или допустимым решением задачи линейного программирования.

Совокупность всевозможных допустимых решений (планов) задачи называют областью допустимых решений задачи.

Оптимальным планом или оптимальным решением задачи линейного программирования называется план, доставляющий наибольшее (наименьшее) значение линейной функции (1.3).

Источник

Лекция 1 Задачи линейного программирования

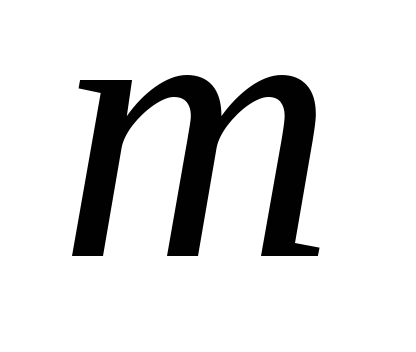
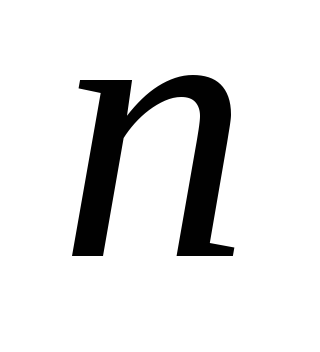
Пусть предприятие из видов ресурсов производитвидов продукции. При этом для производства одной единицыj-го вида продукции расходуетсяединицi-го вида ресурса, т.е.норма расходаi-го ресурса на производствоj-го вида продукции. Матрица, составленная из норм расхода, называется матрицей норм расхода или технологической матрицей.

Обозначим через 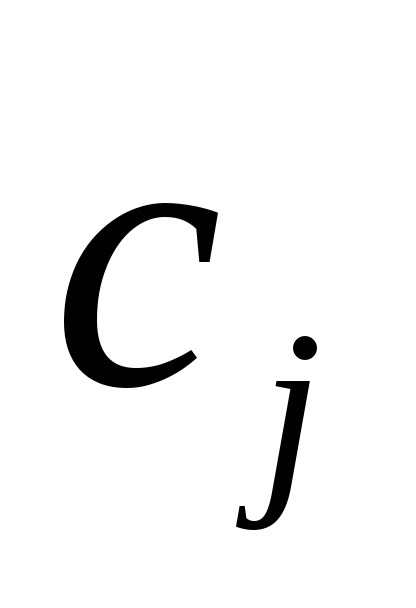величину прибыли от реализации одной единицыj-го вида продукции. Эти значения прибыли запишем матрицей-строкой. План производства продукциих₁,х₂, …,х_побозначим матрицей-столбцомХ. Тогда произведение матрицпредставляет собой величину прибыли, полученной после реализации продукции.

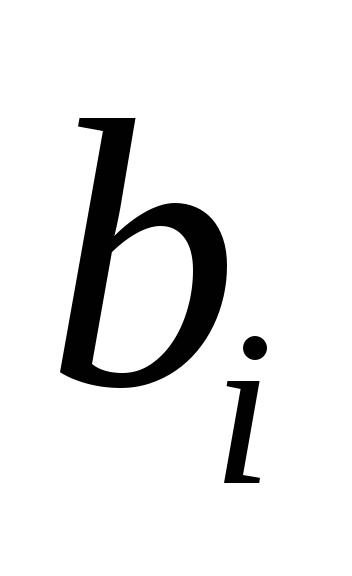
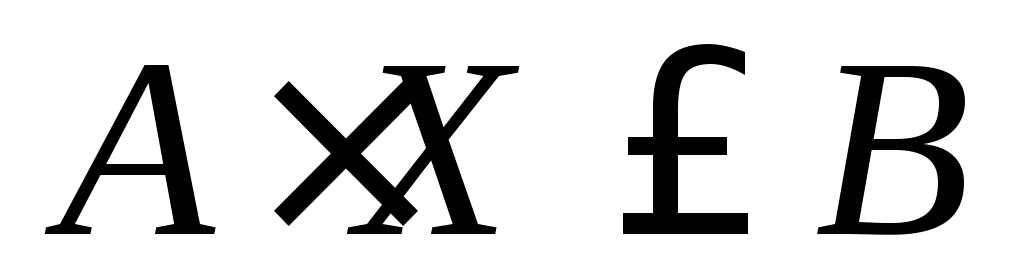
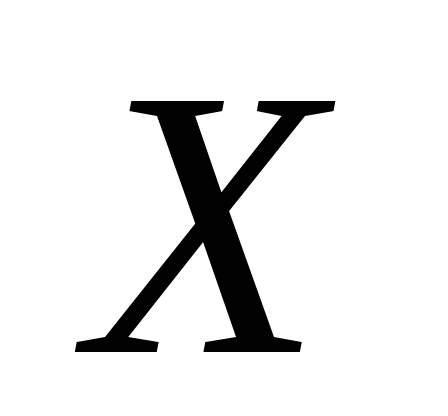
Количество i-го ресурса обозначим. Значенияb₁,b₂, …,b_m запишем матрицей-столбцомB. Тогда матричное неравенствоозначает необходимость, учитывать ограниченность ресурсов при рассмотрении планов производстваХ. Если это неравенство выполняется, то планявляется реальным или допустимым. Естественно, нужно найти такой допустимый план, который бы обеспечил наибольшую прибыль.

Эту задачу можно записать так:

.

,

,.

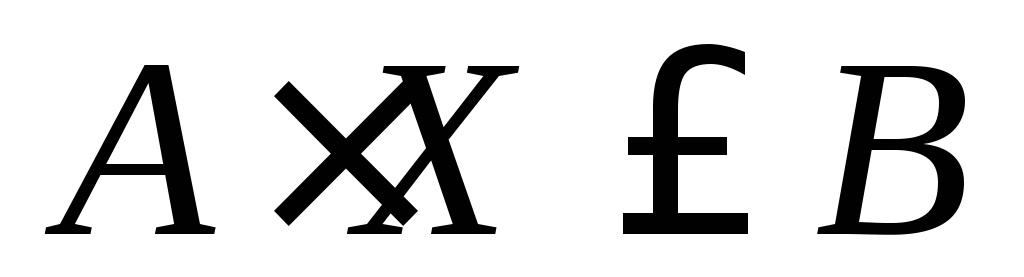
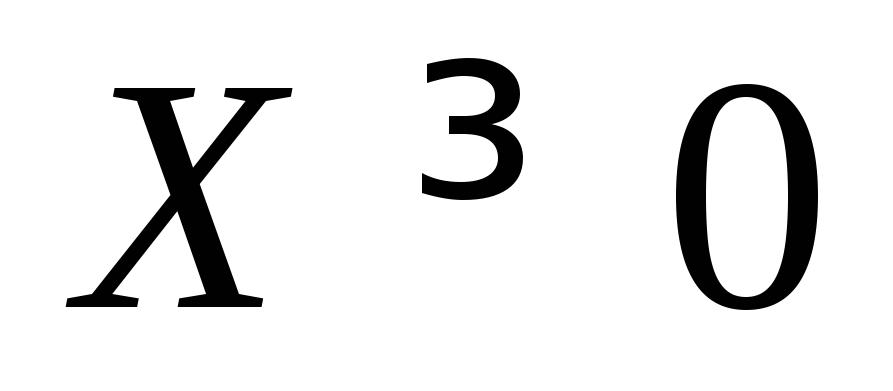
Такая задача называется задачей оптимального планирования производства. Функция называется целевой функцией. Множество всех плановХ, удовлетворяющих неравенствам,, называется множеством допустимых планов, и обозначаетсяD. Тогда нашу задачу можно сформулировать так: найти максимум целевой функциина множестведопустимых планов.

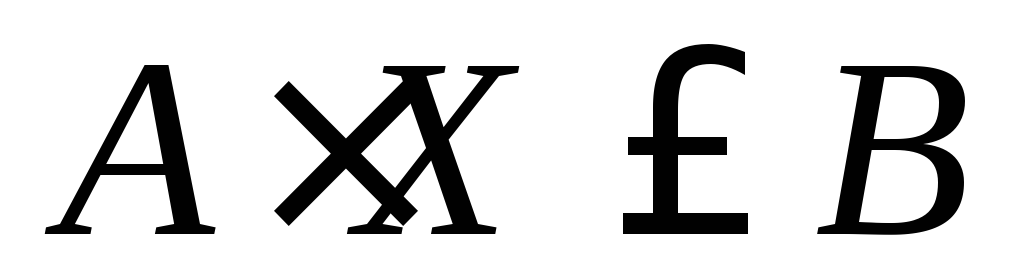
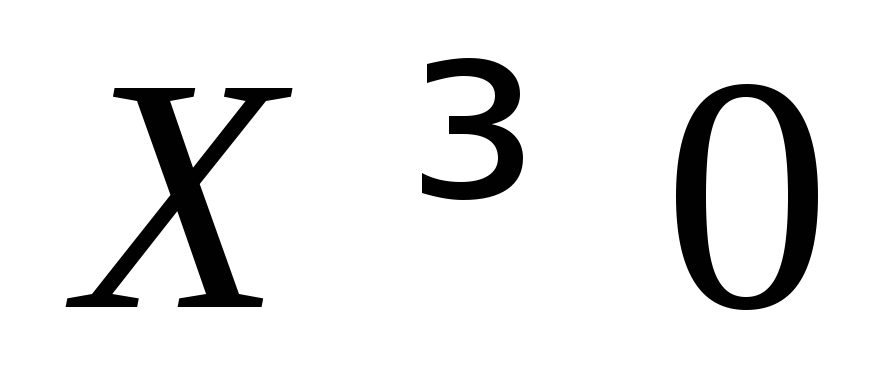
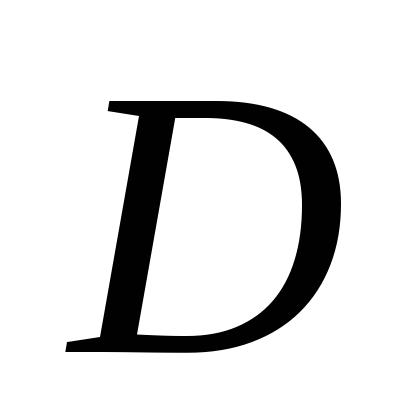
Область ограничений задается линейными функциями. Сама целевая функция также является линейной. Задачи такого вида называются задачами линейного программирования. К ним относятся, например, задачи о диете, о раскрое материала и другие.

Задача линейного программирования в общем виде такова: найти максимум или минимум линейной целевой функции при линейных ограничениях на переменные.

2. Графический метод решения задач линейного программирования

Пусть задача линейного программирования содержит две переменные, 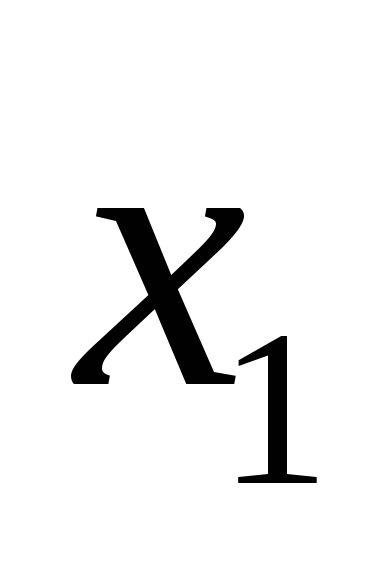и. Графический метод ее решения состоит в следующем.

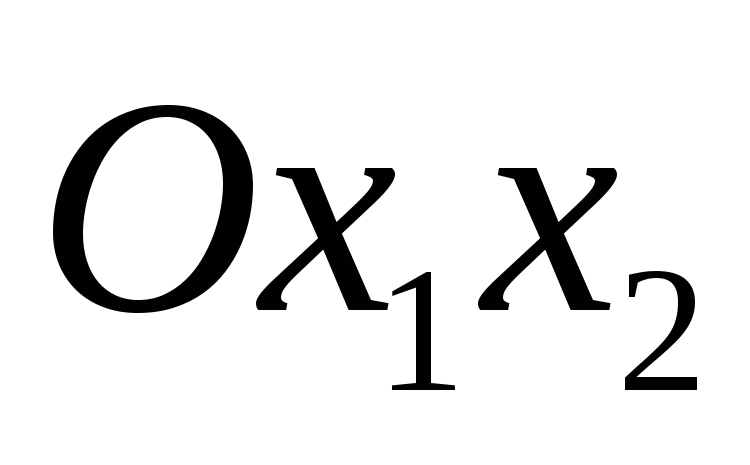
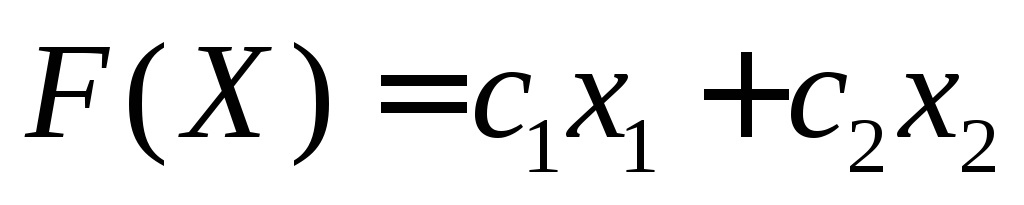
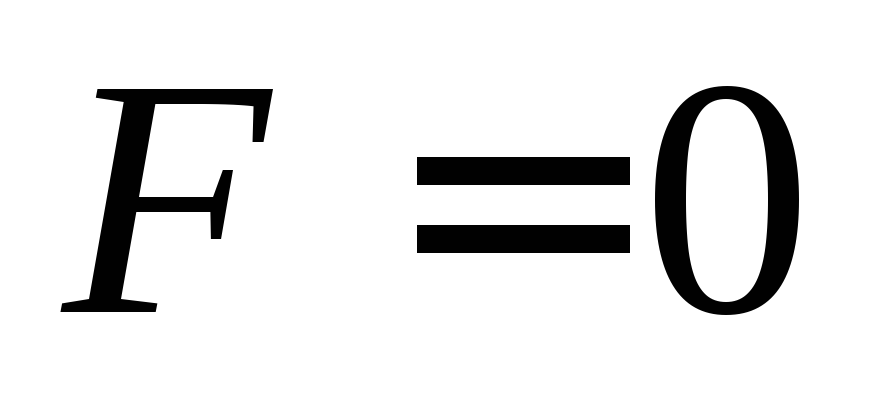
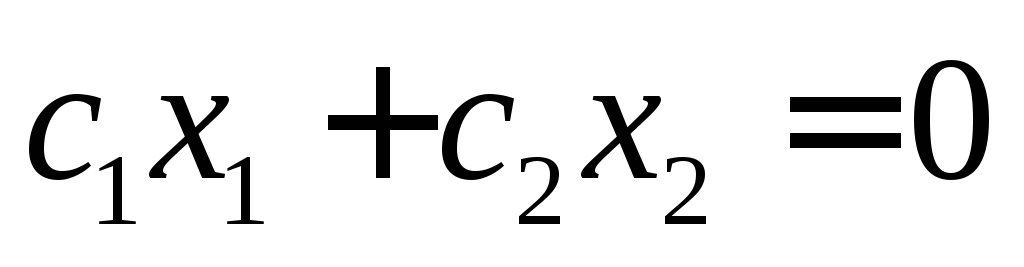
В системе координат строим многоугольник, который определяется системой ограничений. Целевая линейная функцияпри фиксированном значенииявляется уравнением прямой, называемой опорной прямой.

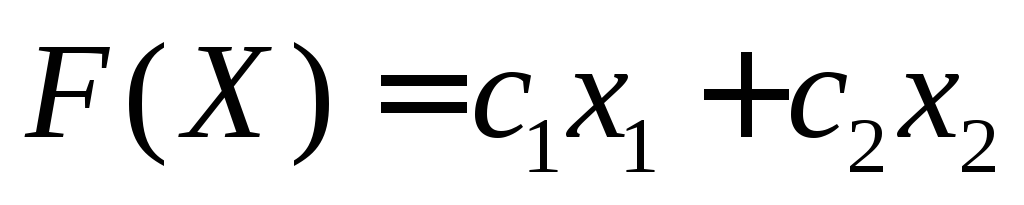
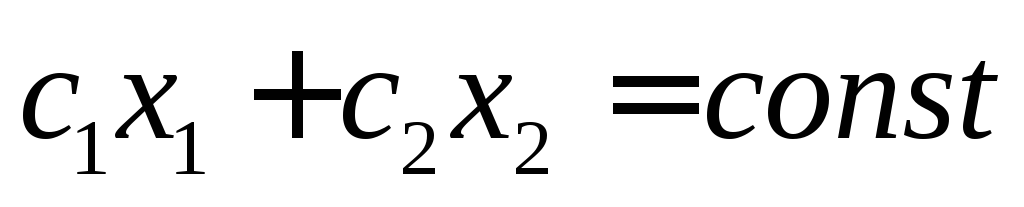
Значение целевой функции возрастает при движении прямойв направлении нормального вектора этой прямой. Перемещая эту прямую параллельно себе в направлении векторапо построенному многоугольнику ограничений, определяем вершины входа и выхода (может быть отрезок или луч).

Вершина, из которой выходит опорная прямая, дает максимальное значение, в которую приходит минимальное значение целевой функции. Определяем координаты этих вершин, и находим соответствующие значения целевой функции, подставляя координаты в выражение для целевой функции.

Пример.Решить графическим методом задачу линейного программирования: найти максимальное значение функциипри ограничениях

,

;

,.

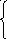
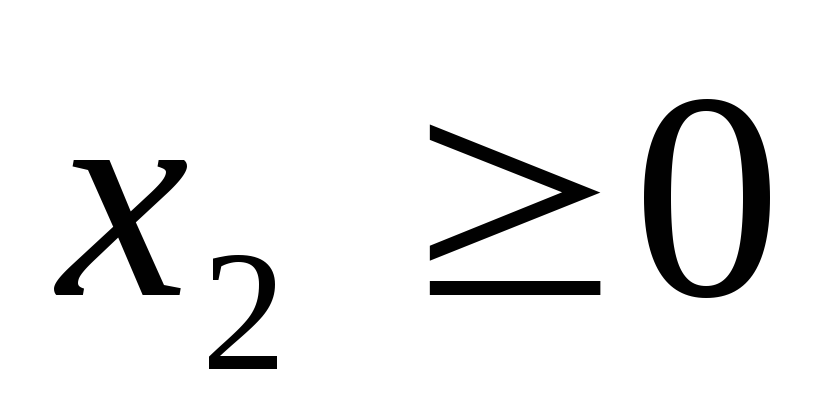
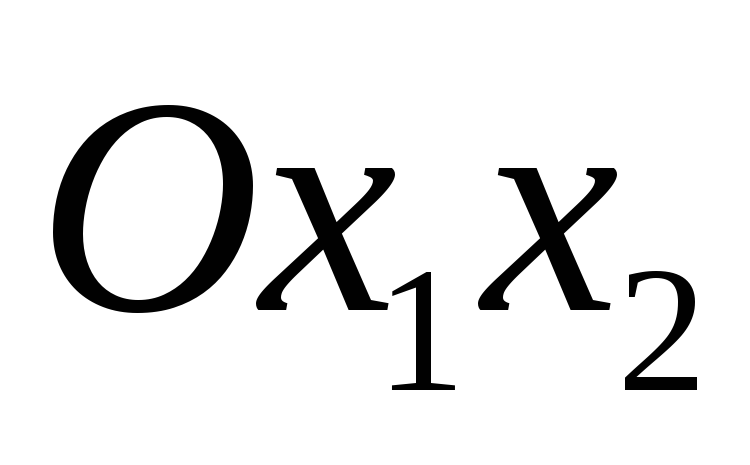
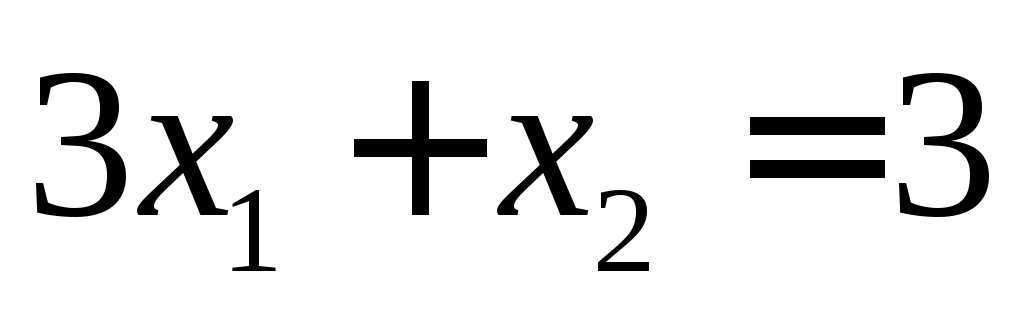
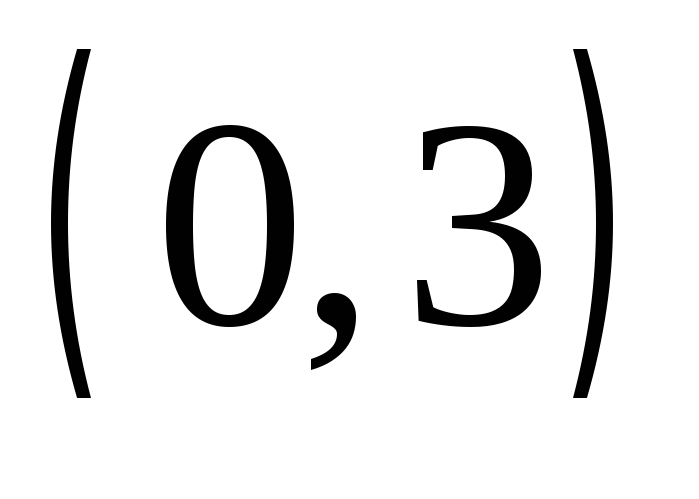
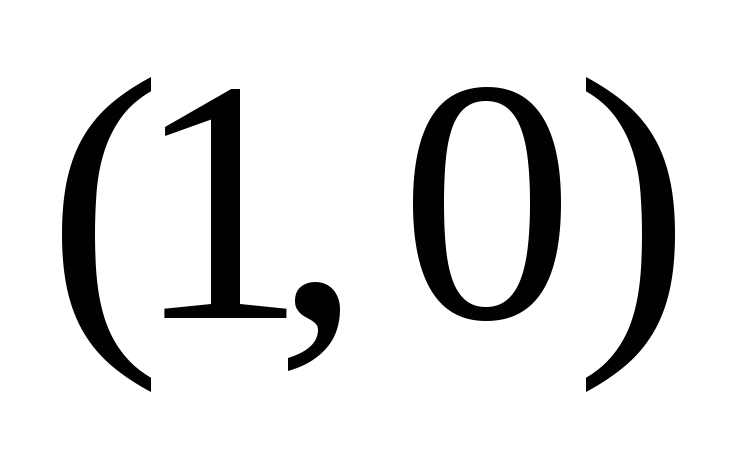
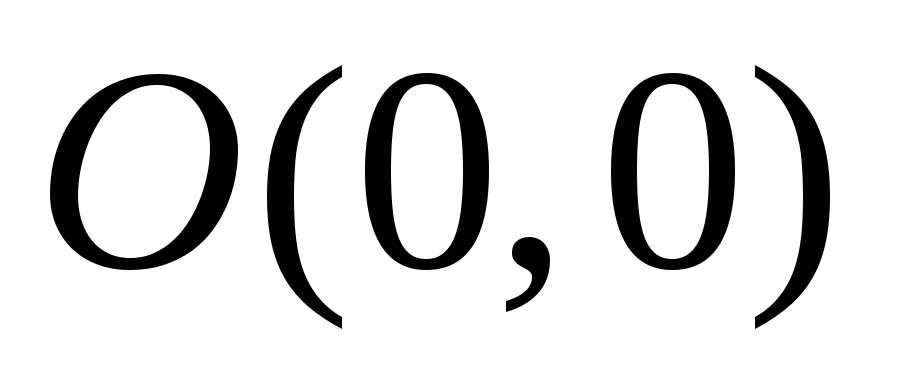
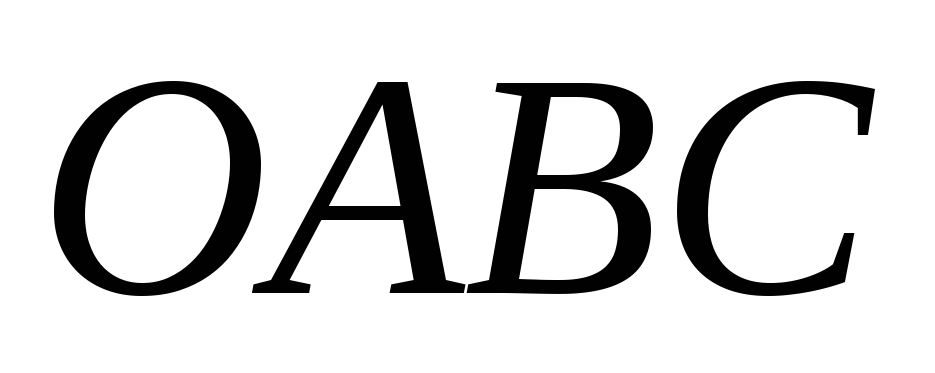
Решение.В системе координатна плоскости строим прямуюпо двум точкам с координатамиив первой четверти, так как. Прямая делит плоскость на две полуплоскости, из которых нужно выбрать одну, удовлетворяющую первому неравенству в системе. Для этого возьмем точкуи подставим в неравенство. Если неравенство выполняется, то нужно заштриховать ту полуплоскость, в которой находится точка. Аналогично поступают с прямой. Получаем, что областью решений неравенств является четырехугольник.

Строим опорную прямую 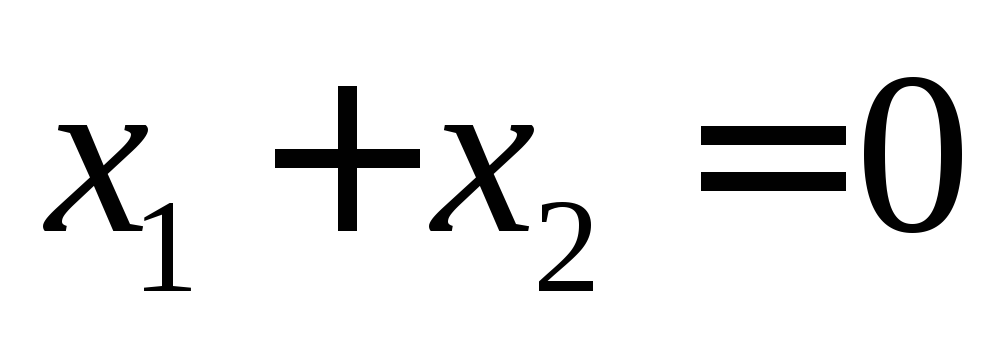, и перемещаем ее параллельно себе в направлении векторапо четырехугольнику, определяем вершину выхода – точкуВ.

Находим координаты точки В, для этого решаем систему уравнений:

Найденные координаты точки подставляем в целевую функцию, и определяем максимальное значение:

.

Данное значение можно найти, если подставить координаты вершин четырехугольника в целевую функцию и выбрать среди них максимальное значение.

Источник

3.1.1. Задача планирования производства

Задача планирования производства (или задача об использовании ресурсов) является одной из разновидностей задачи линейного программирования.

Рассмотрим пример подобной задачи.

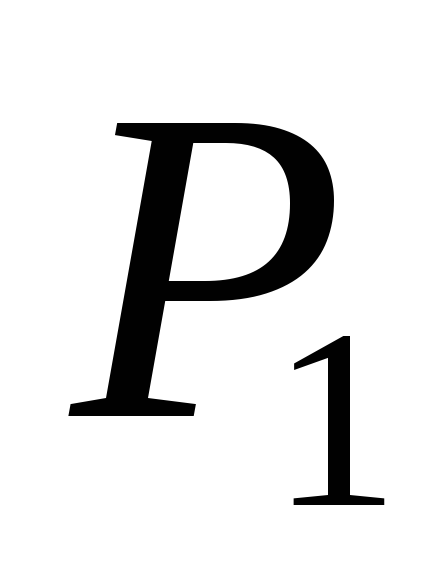
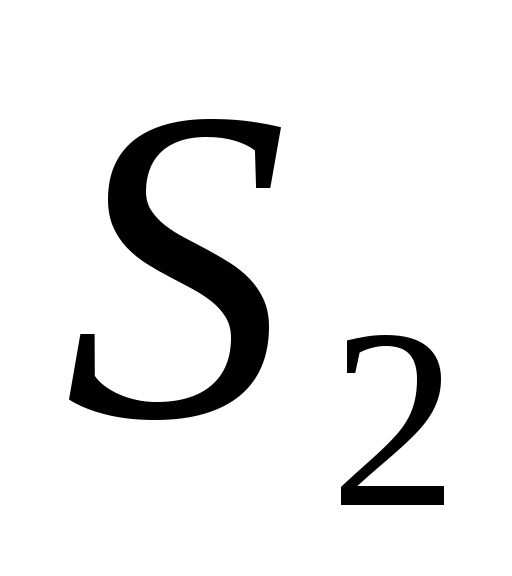
Для изготовления двух видов продукции ииспользуют четыре вида ресурсов,,и. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в табл.1 (цифры условные).

Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции

Число единиц ресурсов, затрачиваемых на изготовление единицы продукции

Прибыль, получаемая от единицы продукции и, – соответственно 2 и 3 руб.

Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной.

Решение. Составим экономико-математическую модель задачи.

Обозначим ,– число единиц продукции соответственнои, запланированных к производству. Для их изготовления потребуетсяединиц ресурса,единиц ресурса,единиц ресурсаиединиц ресурса. Так как потребление ресурсов,,ине должно превышать их запасов, соответственно 18, 16, 5 и 21 единицы, то связь между потреблением ресурсов и их запасами выразится системой неравенств:

(3.1.4)

По смыслу задачи переменные

(3.1.5)

Суммарная прибыль составитруб. от реализации продукцииируб.– от реализации продукции, т.е.

. (3.1.6)

Итак, экономико-математическая модель задачи: найти такой план выпуска продукции , удовлетворяющий системе (3.1.4) и условию (3.1.5), при котором функция (3.1.6) принимает максимальное значение.

Задачу легко обобщить на случай выпуска видов продукции с использованиемвидов ресурсов.

Обозначим – число единиц продукции, запланированной к производству;– запас ресурса,– число единиц ресурса, затрачиваемого на изготовление единицы продукции(числачасто называют технологическими коэффициентами);– прибыль от реализации единицы продукции.

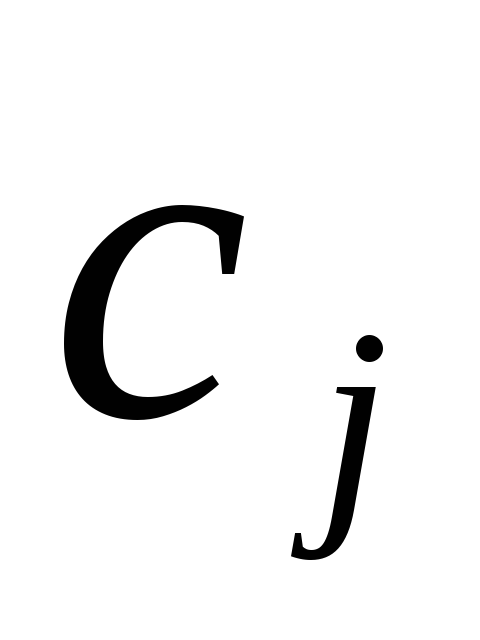
Тогда экономико-математическая модель задачи об использовании ресурсов в общей постановке примет вид: найти такой план выпуска продукции, удовлетворяющий системе

и условию при котором функцияпринимает максимальное значение.

Решение типового примера

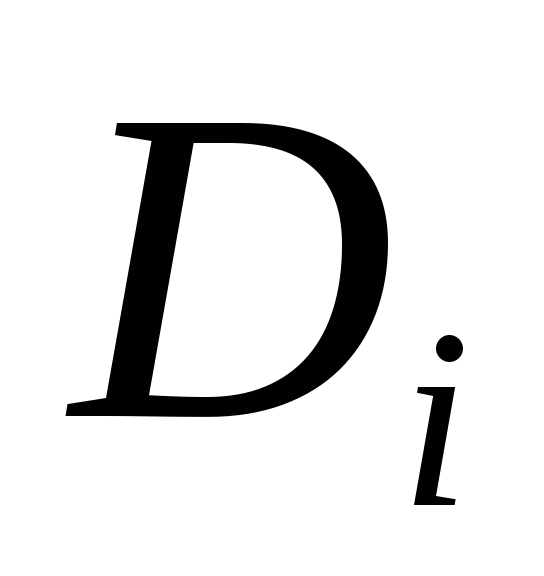
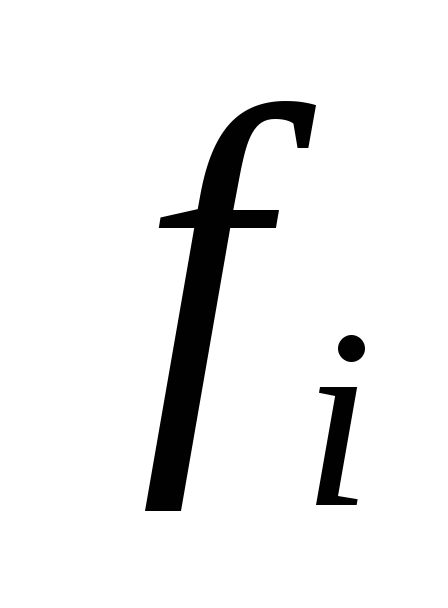
Предприятию ООО «ТИТАН», одним из видов деятельности которого является выполнение токарных, фрезерных и сверлильных работ, поступил заказ на производство гаек стремянки, гаек штанги, гаек МОД и колец шкворня в количестве соответственно шт. Производство заказанной токарной продукции в полном объеме ограничено запасами имеющихся ресурсов (трудозатратами –чел.-час., запасом стали –кг, а также выделенными денежными средствами на оплату труда рабочих и последующую обработку токарной продукции –руб.). Кроме того, известно, что для производства единицы продукции каждого вида требуется соответственнокг стали, трудозатраты при этом составляют соответственночел.-час. За каждую изготовленную деталь рабочий предприятия получаетруб., последующая обработка единицы изделия каждого вида требует затрат денежных средств в размереруб. соответственно.

Задача оптимизации производства для ООО «ТИТАН» ставится в форме максимизации дополнительной прибыли предприятия при заданных ассортименте выпускаемой продукции и ограничениях на имеющиеся запасы ресурсов, при условии, что прибыль от реализации единицы продукции каждого вида составляет соответственно руб.

Исходные данные задачи представлены в табл. 2.

Исходные данные задачи планирования производства

Ассортимент выпускаемой продукции

Источник