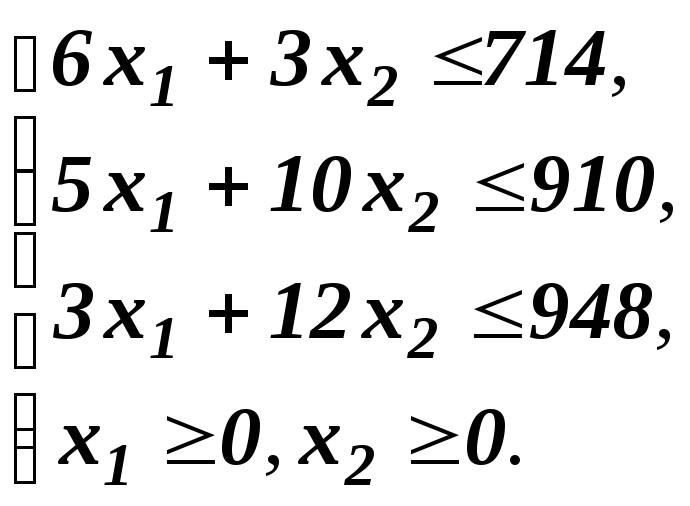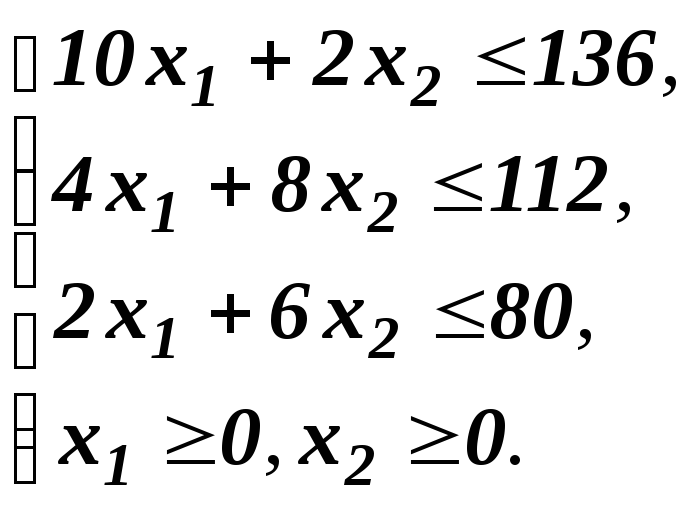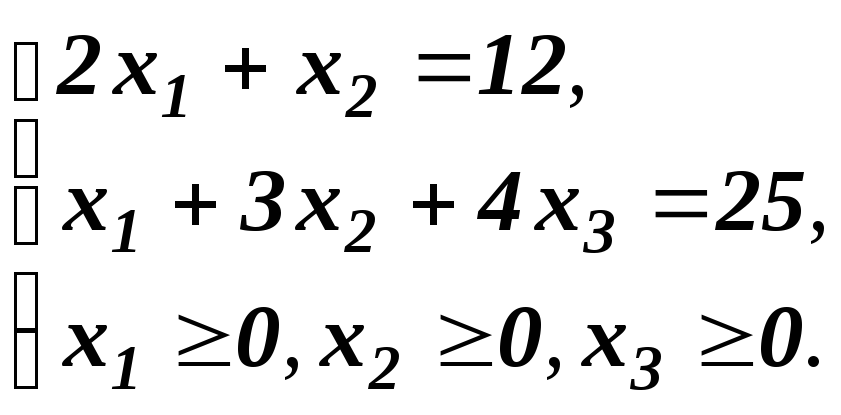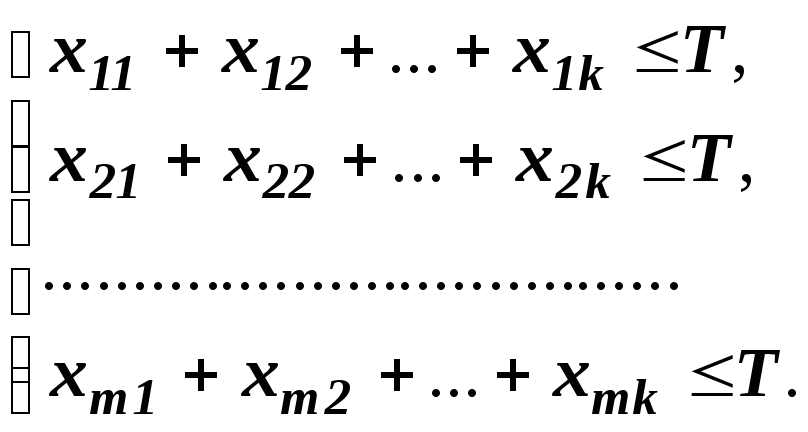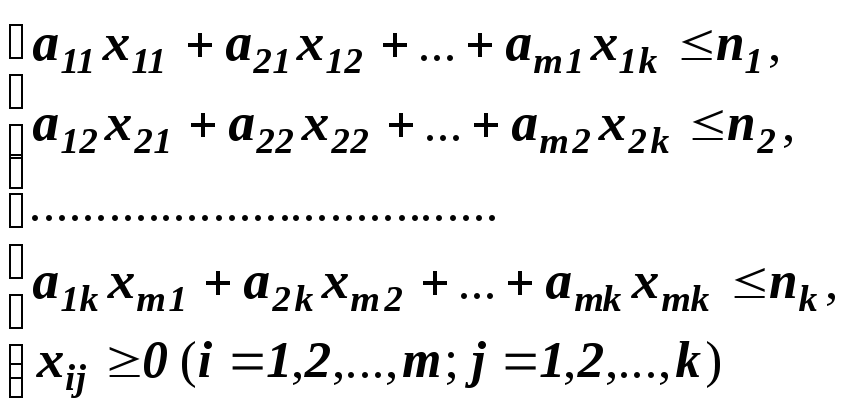Линейное программирование задача об оптимальном использовании ресурсов

1.2.Задача оптимального использования ресурсов.( второй тип )

На сортировочной станции находятся 136 плацкартных вагонов, вмещающих по 48 пассажиров, 112 купейных на 28 мест и 80 мягких, имеющих 24 места. Можно составлять 2 типа поездов: 1 тип состоит из 10 плацкартных, 4 купейных и 2 мягких вагонов, 2 тип — из 2 плацкартных, 8 купейных и 6 мягких. Сколько поездов того и другого типа надо составить, чтобы число пассажиров было максимальным? Если число поездов 1-го типа х₁, а число поездов 2-го типа х₂, то количество используемых плацкартных вагонов равно 10х₁+2х₂, купейных – 4х₁+8х₂, мягких – 2х₁+6х₂. Число пассажиров в поезде первого типа — 640 человек, в поезде второго типа 464 человека. Следова­тельно, задачу можно записать так: найти максимум функции F=640х₁+464x₂, при условии, что

1.3.Задача оптимального раскроя.

В мастерской имеются брусья длиной 1 м. Из них надо выпилить 12 брусков длиной 0.34 м и 25 брусков длиной 0.21 м. Возможны три способа распила.

1 способ: 2 заготовки по 0.34 м и 1 заготовка длиной 0.21 м, в отходы попадает 0.11 м.

2 способ: 1 заготовка по 0.34 м, 3 заготовки длиной 0.21 м, в отхода попадает 0.03 м.

3 способ: 4 заготовки по 0.21 м. в отходы попадает 0.16 м.

Определить, сколько брусьев надо распилить по каждому из возможных вариантов, чтобы общая величина отходов была минимальной. Если x₁ — число брусьев, распиленных первому варианту, х₂ — по второму и х₃ — по третьему, то задачу можно записать следующим образом: найти минимум функции F=0.11х₁+0.03х₂+0.16х₃, при условии, что

1.4. Задача составления рациона ( задача о диете, задача о смесях).

Имеется два вида корма А и В, содержащие питательные вещества (витамины) S₁,S₂ и S₃. В корме вида А содержится 3 ед. вещества S₁, 1 ед. вещества S₂, 1 ед. вещества S₃. В корме вида В содержится 1,2 и 6 ед. веществ S₁,S₂ и S₃ соответственно. Необходимый минимум питательных веществ S₁,S₂ и S₃ составляет 9,8 и 12 ед. Стоимость 1 кг корма А и В соответственно 4 и 6 руб.

Необходимо составить дневной рацион, имеющий минимальную стоимость, в котором содержание каждого вида питательных веществ было бы не менее установленного предела.

Обозначим х₁, х₂ – количество кормов А и В, входящих в дневной рацион. Тогда этот рацион ( 3х₁+х₂ ) ед. питательного вещества S₁, ( х₁+2х₂ ) ед. питательного вещества S₂ и ( х₁+6х₂ ) ед. питательного вещества S₃. Так как содержание питательных веществ в рационе должно быть не менее 9, 8 и 12 ед. соответственно, то получим систему неравенств:

Общая стоимость рациона составит: F=4x₁+6x₂ руб.

Требуется составить такой рацион Х=( х₁,х₂ ), удовлетворяющий указанной системе ограничений, при котором функция F принимает минимальное значение.

1.5.Задача об использовании мощностей (задача о загрузке оборудования).

Предприятию задан план производства продукции по времени и номенклатуре: требуется за время Т выпустить n₁,n₂,…,n_k единиц продукции P₁,P₂,…P_k. Продукция производится на станках S₁,S₂,…S_m. Для каждого станка известны производительность а_ij (т.е. число единиц продукции P_j которое можно произвести на станке S_i) и затраты b_ij на изготовление продукции P_j на станке S_i в единицу времени.

Необходимо составить такой план работы станков (т.е. так распределить выпуск продукции между станками), чтобы затраты на производство всей продукции были минимальными.

Обозначим х_ij – время, в течение которого станок S_i будет занят изготовлением продукции P_j (i=1,2,…m;j=1,2,…k).

Так как время работы каждого станка ограничено и не превышает Т, то справедливы неравенства:

Для выполнения плана выпуска по номенклатуре необходимо, чтобы выполнялись следующие равенства:.

Затраты на производство всей продукции выразятся функцией:

F = b₁₁x₁₁+b₁₂x₁₂+…+b_mkx_mk.

Требуется найти такое решение Х=( х₁₁,х₁₂,…,х_mk ), удовлетворяющее обеим системам ограничений и при котором функция F принимает минимальное значение.

Источник

Пример задачи линейного программирования: задача использования ресурсов, её графическое решение

От общей задачи линейного программирования — к частной

На этом уроке будем учиться решать полностью сформулированную задачу линейного программирования — задачу использования ресурсов и наполнять содержанием основные определения, с которыми ознакомились на уроке «Задача линейного программирования: определения, модели, примеры, основные теоремы«.

В экономико-математических моделях задачи линейного программирования численные решения вводят как неизвестные. Эти неизвестные в наиболее часто встречающихся задачах — о производстве — обозначают, например, виды продукции, которые следует производить в определённом количестве, чтобы получить максимальный доход, или чтобы стоимость их производства была минимальной. Неизвестные обычно записывают в виде буквы x с нижним индексом.

Система ограничений в задаче линейного программирования представляет собой систему линейных неравенств и (или) уравнений. Каждое неравенство или уравнение задаёт ограничение запасов одного из производственных факторов — вида сырья, времени, рабочей силы или чего-либо другого. Коэффициенты при неизвестных, записываемые обычно в виде буквы a с нижними индексами, обозначают количество производственного фактора, расходуемого для производства единицы соответствующего вида продукции. Это количество должно быть заранее известно.

Таким образом, система ограничений записывается в виде

Другой обязательный элемент модели задачи линейного программирования — функция цели. Как и система ограничений, она так же линейна. В функции цели присутствуют те же неизвестные, а коэффициенты при них, обычно записываемые в виде буквы c с нижними индексами, могут обозначать заранее известный доход от реализации единицы соответствующего вида продукции, а могут, как в задачах о расходе производственнных мощностей или в задаче о питании, обозначать расходы. Записывается функция цели в следующем виде:

Если функция цели задаёт доходы, то в задаче требуется найти максимум этой функции, если задаёт расходы, то требуется найти минимум.

Каждый вариант численных значений неизвестных, который удовлетворяет системе ограничений задачи линейного программирования, называется планом или программой. Показателем эффективности плана является всё та же функция цели. В каждой задаче линейного программирования может быть только одна функция цели. План, который соответствует максимуму или минимуму (то есть, в общем случае, оптимуму) функции цели, называется оптимальным планом.

Переменные в задаче использования ресурсов

Для изготовления двух видов продукции и требуется четыре вида ресурсов (сырья): , , , . Запасы сырья — соответственно , , , единицы.

Доход от реализации одной единицы продукции равен у. е., а доход от реализации одной единицы продукции равен у. е. Требуется получить наибольший доход от изготовления продукции и , то есть, узнать, сколько единиц и сколько единиц нужно изготовить из имеющегося запаса сырья, чтобы получить максимальный доход.

Запишем задачу использования ресурсов в виде математических соотношений. Для удобства сначала запишем все данные в виде таблицы.

Виды сырья	Запасы сырья	Виды продукции
		Доход от реализации одной единицы продукции

Система ограничений в задаче использования ресурсов

Количество единиц продукции обозначим через , а количество единиц продукции — через .

Тогда на основании таблицы запишутся неравенства (ограничения):

В самом деле, для изготовления каждой единицы продукции необходимо единиц сырья , а для изготовления единиц требуется единиц сырья . Для изготовления единиц продукции требуется единиц сырья . Так как запасы сырья составляют , то расход не может превышать . В результате получим первое неравенство . Из остальных строк таблицы составили ещё 3 неравенства приведённой выше системы.

Что является решением задачи использования ресурсов

Доход от реализации единиц продукции по у. е. за каждую единицу составляет у. е., аналогично доход от реализации единиц продукции по у. е. за каждую единицу составит у. е. Тогда суммарный доход от реализации обоих видов продукции и запишется в виде . В задаче требуется вычислить максимальный доход, то есть найти .

Пример решения задачи графическим методом

Задача. Для изготовления столов и шкафов используется два вида древесины: и . Для изготовления одного шкафа используется древесины и древесины . Для изготовления одного стола используется древесины и древесины . Доход мастерской от производства одного стола составляет 12 у. е., от производства одного шкафа — 15 у. е. Определить, сколько столов и сколько шкафов должна изготовить мастерская, чтобы обеспечить наибольшую рентабельность их производства, если в распоряжении мастерской имеется древесины , а древесины .

Решение. Составим таблицу.

Вид древесины	Вид изделия
	стол	шкаф	запасы
0,15	0,2	60
0,2	0,1	40
Доход	12	15

Количество столов обозначим через , количество шкафов — . Тогда из таблицы легко составить систему ограничений :

Найдём максимум C при условиях . Для удобства неравенства умножим на 100. Получим

Сокращая первое неравенство на 5, а второе на 10, получим

Далее, для упрощения вычислений введём масштаб 1:100, то есть, в правых частях последней системы неравенств отбросим по два нуля, тогда система запишется в виде

Строим многоугольник решений системы. Для этого построим на координатной плоскости прямые, заданные уравнениями системы. Для этого надо знать какие-либо две точки этой прямой. Ищем точки пересечения каждой прямой с осью абсцисс, подставляя значение в соответствующее уравнение. Затем ищем точки пересечения каждой прямой с осью ординат, поставляя значение . Ясно, что решениями системы могут быть только положительные решения. Поэтому многоугольником решений будет четырёхугольник . Теперь ищем значение максимума функции цели. Линейная форма геометрически означает семейство параллельных между собой прямых. Среди прямых этого семейства есть опорные прямые mn и MN. Это такие прямые, которые имеют с многоугольником хотя бы одну точку и многоугольник целиком лежит по одну сторону от этой прямой. Как видно из рисунка, прямая mn является опорной, так как она касается многоугольника в точке О и многоугольник целиком лежит правее (или выше) этой прямой. Прямая MN также является опорной, так как имеет с многоугольником общую точку В и многоугольник целиком лежит левее (или ниже) этой прямой. Из рисунка видно, что функция цели достигает максимума в точке B (80, 240) (не забываем про масштаб). Подставляя координаты точки в функцию цели, имеем

Таким образом, максимум дохода в сумме 4560 у. е. мастерская получит, если изготовит 80 столов и 240 шкафов.

Источник

2. Задача об оптимальном использовании ресурсов при производственном планировании.

Общий смысл задач этого класса сводится к следующему.

Предприятие выпускает n различных изделий. Для их производства требуется m различных видов ресурсов (сырья, материалов, рабочего времени и т.п.). Ресурсы ограничены, их запасы в планируемый период составляют, соответственно, b₁, b₂. b_m условных единиц.

Известны также технологические коэффициенты a_ij, которые показывают, сколько единиц i-го ресурса требуется для производства единицы изделия j-го вида ( ).

Прибыль, получаемая предприятием при реализации изделия j-го вида, равна c_j.

В планируемом периоде значения величин a_ij, b_i и c_j остаются постоянными.

Требуется составить такой план выпуска продукции, при реализации которого прибыль преприятия была бы наибольшей.

Далее приведем простой пример задачи такого класса.

Компания специализируется на выпуске хоккейных клюшек и наборов шахмат. Каждая клюшка приносит компании прибыль в размере $2, а каждый шахматный набор — в размере $4. На изготовление одной клюшки требуется четыре часа работы на участке A и два часа работы на участке B. Шахматный набор изготавливается с затратами шести часов на участке A, шести часов на участке B и одного часа на участке C. Доступная производственная мощность участка A составляет 120 н-часов в день, участка В — 72 н-часа и участка С — 10 н-часов.

Сколько клюшек и шахматных наборов должна выпускать компания ежедневно, чтобы получать максимальную прибыль?

Условия задач указанного класса часто представляют в табличной форме (см. таблицу 2.1).

Таблица 2.1 — Исходные данные задачи об использовании производственных ресурсов

производственные участки

затраты времени на единицу продукции, н-час

доступный фонд времени, н-час

Источник