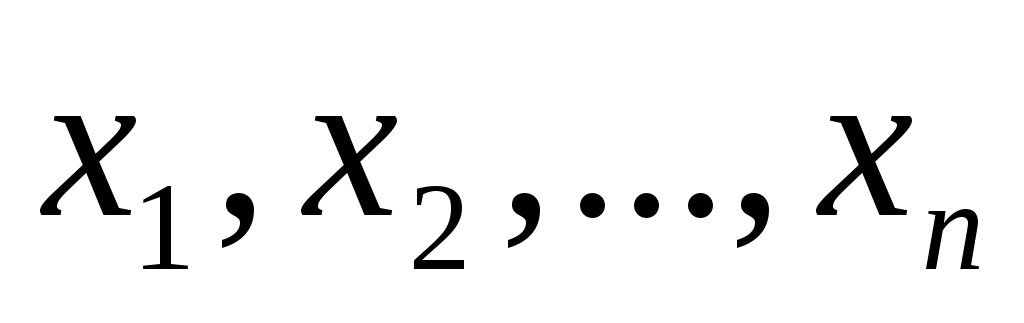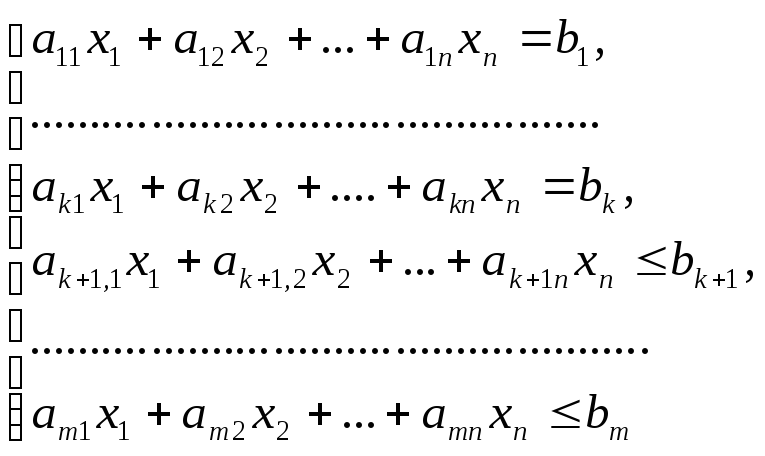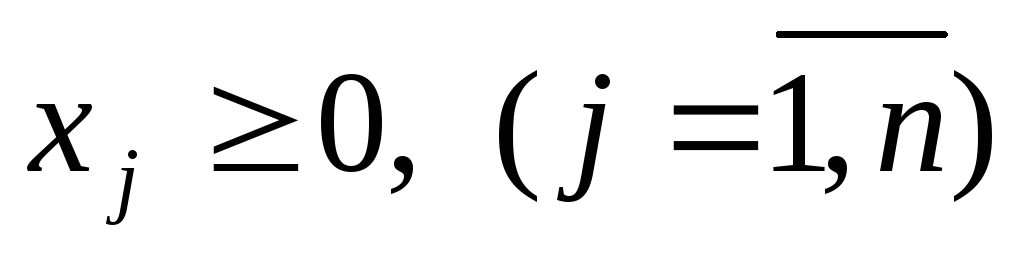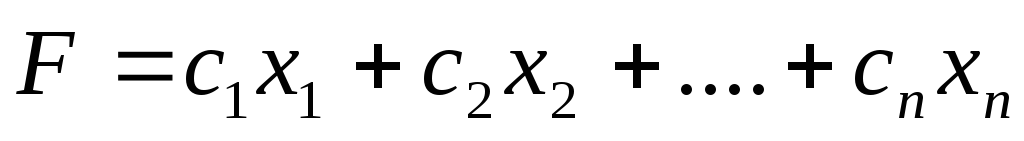2. Задача об оптимальном использовании ресурсов при производственном планировании.
Общий смысл задач этого класса сводится к следующему.
Предприятие выпускает n различных изделий. Для их производства требуется m различных видов ресурсов (сырья, материалов, рабочего времени и т.п.). Ресурсы ограничены, их запасы в планируемый период составляют, соответственно, b1, b2. bm условных единиц.
Известны также технологические коэффициенты aij, которые показывают, сколько единиц i-го ресурса требуется для производства единицы изделия j-го вида ( ).
Прибыль, получаемая предприятием при реализации изделия j-го вида, равна cj.
В планируемом периоде значения величин aij, bi и cj остаются постоянными.
Требуется составить такой план выпуска продукции, при реализации которого прибыль преприятия была бы наибольшей.
Далее приведем простой пример задачи такого класса.
Компания специализируется на выпуске хоккейных клюшек и наборов шахмат. Каждая клюшка приносит компании прибыль в размере $2, а каждый шахматный набор — в размере $4. На изготовление одной клюшки требуется четыре часа работы на участке A и два часа работы на участке B. Шахматный набор изготавливается с затратами шести часов на участке A, шести часов на участке B и одного часа на участке C. Доступная производственная мощность участка A составляет 120 н-часов в день, участка В — 72 н-часа и участка С — 10 н-часов.
Сколько клюшек и шахматных наборов должна выпускать компания ежедневно, чтобы получать максимальную прибыль?
Условия задач указанного класса часто представляют в табличной форме (см. таблицу 2.1).
Таблица 2.1 — Исходные данные задачи об использовании производственных ресурсов
производственные участки
затраты времени на единицу продукции, н-час
доступный фонд времени, н-час
1.1 Линейное программирование как метод оптимального планирования
Линейное программирование (ЛП) изучает важную для практики задачу отыскания экстремума линейной функции при наличии ограничений в виде линейных неравенств или уравнений.
Сущность этих задач заключается в том, чтобы из множества различных вариантов исследуемого экономического процесса, выбрать по какому-либо признаку наилучший, или, как его называют, оптимальный вариант.
В этом методе обязателен специальный показатель выгодности плана, который называют показателем или критерием оптимального плана. Часто это прибыль, доход, валовый продукт, производительность, эффективность. В таких случаях выгодно, чтобы показатель оптимальности для выбранного плана был максимальным. Если показателем оптимальности плана служат издержки, себестоимость, капиталовложения или трудоемкость, то необходимо планировать так, чтобы показатель оптимальности для выбранного плана был минимальным.
Таким образом, ясно, что цель, которую мы ставим перед собой, заключается в максимизации или минимизации некоторого количества средств (денег, сырья, оборудования, продуктов питания), которое математически выражается в виде линейной формы некоторого числа переменных.
Множество возможных вариантов, из которых выбирается оптимальный план, всегда ограничено (ресурсами сырья, наличием рабочей силы, количеством оборудования и т. п.), поэтому каждый из рассматриваемых вариантов должен быть допустимым планом, удовлетворяющим имеющимся ограничениям. Показатель оптимальности плана является некоторой функцией 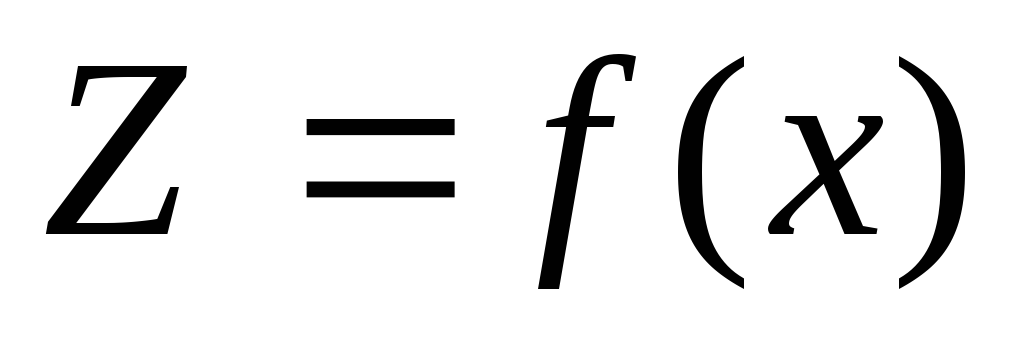
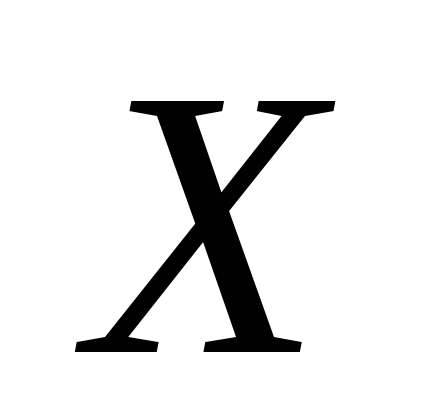
Решение экстремальных экономических задач можно разбить на 3 этапа: 1) построение экономико-математической модели; 2) нахождение оптимального решения одним из математических методов; 3) практическое внедрение.
Построение экономико-математической модели состоит в создании упрощенной экономической модели, в которой в схематической форме отражена сущность изучаемого процесса. При этом особое внимание должно быть уделено отражению в модели всех существенных особенностей задачи и учету всех ограничивающих условий, которые могут повлиять на результат. Затем определяют цель решения, выбирают критерий оптимальности и дают математическую формулировку задачи.
1.2 Общая задача линейного программирования
Общую задачу линейного программирования можно сформулировать следующим образом. Найти такие значения , которые удовлетворяют системе ограничений
(1.1)
(1.2)
и для которых линейная функция (целевая функция)
(1.3)
достигает экстремума (максимума или минимума).
Вектор , координаты которого удовлетворяют системе (1.1) и (1.2) называют опорным планом или допустимым решением задачи линейного программирования.
Совокупность всевозможных допустимых решений (планов) задачи называют областью допустимых решений задачи.
Оптимальным планом или оптимальным решением задачи линейного программирования называется план, доставляющий наибольшее (наименьшее) значение линейной функции (1.3).
Линейное программирование оптимальный план производства
Целями данного урока является не изложение теории из курса матпрограммирования, а более простая цель — показать практическое применение знаний, которые Вы получаете в процессе изучения раздела «математическое программирование» в курсе высшей математики. Поэтому изложение будет максимально простым, но не совсем «каноническим».
Задача
Предприятие планирует выпускать четыре вида продукции. Объемы ресурсов трех видов (в расчете на трудовую неделю), затраты каждого ресурса на изготовление единицы продукции и цена единицы продукции приведены в таблице. Найти, сколько продукции и какого вида необходимо производить, чтобы общая выручка от реализации всей выпущенной продукции была бы наибольшей. Построить модель прямой и двойственной задач. Найти оптимальные планы для обеих задач и экстремальные значения целевых функций. Дать экономическую интерпретацию основным и дополнительным переменным исходной и двойственной задач. Проанализировать рациональность расширения ассортимента продукции за счет включения новой продукции (П5).
| П1 | П2 | П3 | П4 | Объем | П5 | |
| Р1 | 8 | 10 | 8 | 10 | 3600 | 9 |
| Р2 | 4 | 7 | 4 | 6 | 1850 | 5 |
| Р3 | 4 | 3 | 3 | 5 | 1500 | 3 |
| Цена | 25 | 30 | 40 | 35 | 33 |
Решение .
Обозначим через x1..x4 число изготавливаемых продуктов. Тогда условие задачи может быть записано в следующем виде:
Припишем каждому из видов сырья, используемых для производства продукции, двойственную оценку, соответственно равную y1, y2 и у3. Тогда общая оценка сырья, используемого на производство продукции, составит
Согласно условию, двойственные оценки должны быть такими, чтобы общая оценка сырья, используемого на производство единицы продукции каждого вида, была не меньше цены единицы продукции данного вида, т. е. y1, y2 и у3 должны удовлетворять следующей системе неравенств:
8y1 + 4y2+ 4y3 ≥ 25
10y1 + 7y2+ 3y3 ≥ 30
8y1 + 4y2+ 3y3 ≥ 40
10y1 + 6y2+ 5y3 ≥ 35
y1 ≥ 0
y2 ≥ 0
y3 ≥ 0
Как видно, данные задачи образуют симметричную пару двойственных задач. Решение прямой задачи дает оптимальный план производства изделий, а решение двойственной – оптимальную систему оценок сырья, используемого для производства этих изделий. Чтобы найти решение этих задач, следует сначала отыскать решение какой–либо одной из них.
Приведем математическую модель задачи к каноническому виду.Для этого избавимся от знаков неравенств посредством ввода дополнительных переменных и замены знака неравенства на знак равенства. Дополнительная переменная добавляется для каждого неравенства, причем эта переменная указывается в целевой функции с нулевым коэффициентом. Правило ввода дополнительных переменных: при «>=» — переменная вводится в неравенство с коэффициентом (-1); при »
Экономический смысл введенных дополнительных переменных — остатки соответствующих ресурсов каждого вида. Для решения задачи составим симплекс-таблицу.
Симплекс-таблица составляется так:
В графе «Базис» записываются вектора переменных, принимаемые за базисные. На первом этапе это – A5, A6, A7. Базисными будут переменные, каждая из которых входит только в одно уравнение системы, и нет такого уравнения, в которое не входила бы хотя бы одна из базисных переменных.
В следующий столбец записываются коэффициенты целевой функции, соответствующие каждой переменной. Столбец В – столбец свободных членов. Далее идут столбцы коэффициентов Аi при i –й переменной.
| 25 | 30 | 40 | 35 | 0 | 0 | 0 | ||||
| i | Базис | C | B | A1 | A2 | A3 | A4 | A5 | A6 | A7 |
| 1 | A5 | 0 | 3600 | 8 | 10 | 8 | 10 | 1 | 0 | 0 |
| 2 | A6 | 0 | 1850 | 4 | 7 | 4 | 6 | 0 | 1 | 0 |
| 3 | A7 | 0 | 1500 | 4 | 3 | 3 | 5 | 0 | 0 | 1 |
| 4 | Fi-Ci | 0 | -25 | -30 | -40 | -35 | 0 | 0 | 0 |
Под столбцом свободных членов записывается начальная оценка F0 = CiBi = 0*3600+0*1850+0*1500=0 .
Остальные оценки записываются под столбцами соответствующих векторов:
F1 — C1 = 0*8 + 0*4 + 0*4 — 25 = -25
F2 — C2 = 0*10 + 0*7 + 0*3 — 30 = -30
F3 — C3 = 0*8 + 0*4 + 0*3 — 40 = -40
F4 — C4 = 0*10 + 0*6 + 0*5 — 35 = -35
Следует отметить, что оценки для базисных векторов всегда равны нулю.
Преобразование симплекс-таблицы ведется следующим образом:
Шаг 1 : Проверяется критерий оптимальности, суть которого состоит в том, что все оценки должны быть неотрицательны. В нашем случае этот критерий не выполнен, поэтому переходим ко второму шагу.
Шаг 2 : Для отрицательных оценок вычисляются величины:
Из этих элементов выбирается тот, для которого вычисленное произведение минимально, в нашем случае минимально -18000, поэтому выбираем третий столбец, а в качестве так называемого разрешающего элемента выбирается первый элемент третьего столбца (по значению Θ3 ) – 8 (выделен в таблице).
Шаг 3 : Третья строка таблицы делится на 8 и вычитается из остальных строк с коэффициентами, позволяющими ввести в базис третий столбец. В сущности, применяется метод исключения неизвестных, известный как метод Жордана – Гаусса..
| 25 | 30 | 40 | 35 | 0 | 0 | 0 | ||||
| i | Базис | C | B | A1 | A2 | A3 | A4 | A5 | A6 | A7 |
| 1 | A3 | 40 | 450 | 1 | 1,25 | 1 | 1,25 | 1/8 | 0 | 0 |
| 2 | A6 | 0 | 12.5 | 0 | 0.5 | 0 | 0.25 | -1/8 | 0.25 | 0 |
| 3 | A7 | 0 | 50 | 1/3 | -0,25 | 0 | 5/12 | -1/8 | 0 | 1/3 |
| 4 | Fi-Ci | 0 | 15 | 20 | 0 | 15 | 5 | 0 | 0 | |
В итоге получаем все положительные оценки Fi — Ci, что означает оптимальность полученного плана. То есть необходимо выпускать 450 единиц продукции третьего вида, чтобы выручка была максимальной и составляла 18 тысяч.
Проанализируем, что будет, если включить в ассортимент пятый вид товара.
Приведем математическую модель задачи к каноническому виду.
| 25 | 30 | 40 | 35 | 33 | 0 | 0 | 0 | ||||
| i | Базис | C | B | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 |
| 1 | A6 | 0 | 3600 | 8 | 10 | 8 | 10 | 9 | 1 | 0 | 0 |
| 2 | A7 | 0 | 1850 | 4 | 7 | 4 | 6 | 5 | 0 | 1 | 0 |
| 3 | A8 | 0 | 1500 | 4 | 3 | 3 | 5 | 3 | 0 | 0 | 1 |
| 4 | Fi-Ci | 0 | -25 | -30 | -40 | -35 | -33 | 0 | 0 | 0 | |
Из этих элементов выбирается тот, для которого вычисленное произведение минимально, в нашем случае минимально -18000, поэтому выбираем третий столбец, а в качестве так называемого разрешающего элемента выбирается первый элемент третьего столбца (по значению Θ3 ) – 8 (выделен в таблице).
| 25 | 30 | 40 | 35 | 33 | 0 | 0 | 0 | ||||
| i | Базис | C | B | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 |
| 1 | A3 | 40 | 450 | 1 | 1.25 | 1 | 1,25 | 1,125 | 1/8 | 0 | 0 |
| 2 | A7 | 0 | 12,5 | 0 | 0,5 | 0 | 0,25 | 1/8 | -1/8 | 1/4 | 0 |
| 3 | A8 | 0 | 50 | 1/3 | -0,25 | 0 | 5/12 | -1/8 | -1/8 | 0 | 1/3 |
| 4 | Fi-Ci | 0 | 15 | 20 | 0 | 15 | 12 | 5 | 0 | 0 | |
В итоге получаем все положительные оценки Fi — Ci, что означает оптимальность полученного плана. То есть необходимо выпускать 450 единиц продукции третьего вида, чтобы выручка была максимальной и составляла 18 тысяч.
Таким образом, введение нового продукта никак не повлияет на стратегию предприятия по максимизации выручки.