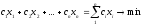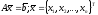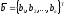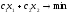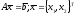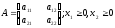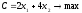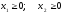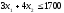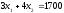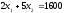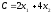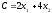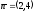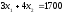Линейное моделирование динамическое программирование имитационные модели

5.Виды имитационных моделей.

Статистическое (позволяет прогнозировать развитие явления, позволяет понять направления развития) Агентное(отличается от других тем, что в ней задаются, характеристики отдельных ее объектов (агентов), а общая характеристика работы системы и общая динамика складываются из наложения друг на друга характеристик агентов. Моделирование динамических систем (это поведение системы во времени в пространстве. моделируется процесс сборки урожая) Системная динамика (модели потокового типа, непрерывное моделирование. Решение систем дифференциальных уравнений) Дискретно-событийное (предполагает решение задач относительно работы СМО) Экспертное Ситуационное(это поиск наиболее оптимального плана действий в условиях возникновения непредвиденных ситуаций) Когнетивное (аналогичен методу системной динамики, только в нем закладываются специфические объекты, в нее вкл элементы которые рассчитываются на основе знаний, представлений. Когнетивное мод – предполагает создание когнетивных карт)

6.Модельное время, способы его продвижения.

В имит мод обязательно присутствует переменная времени. Процессы моделируются в динамике в соответствии с шагом модельного времени. Шаг это может быть сек, мин, год, и на каждый дельта t система меняется. Горизонт моделирования – это моделируемое время работы системы (наприм. Парикмахерская работает 8 ч.) В отдельных концептуальных моделях состояние системы фиксируется дискретно (прерывисто) от шага к шагу, это м б выраженно на графике. Дельта tможет быть с постоянным шагом, а м б с переменным. Способ изменения состояния системы м б пошаговым или пособытийным. Пошаговый способ применяется когда события происходят часто. (наприм. Приход клиента в магазин) Пособытийный способ используется когда события происходят редко, нет необходимости фиксировать каждый шаг модельного времени. Основная масса систем имит мод предполагает равный шаг модельного времени. С помощью этих шагов система переходит из одного состояния в другое, в модели синхронизируются все процессы. С помощью модельного времени происходит управление ходом моделирования. Другие концепции реализуется с помощью программ отражающих непрерывное изменение системы от шага к шагу.

7.Концепции имитационного моделирования.

Существует 3 концепции: Дискретно-событийная, системная динамика и агентное. Дискрет-соб предполагает решение задач относительно работы СМО. Системная динамика – это модели потокового типа, непрерывное моделирование. Системы дифур. Агентноеотличается от других тем что в ней задаются характеристики отдельных объектов (агентов) а общая хар-ка работы системы и общая динамика складываются из наложения друг на друга хар-к объектов.

8.Метод статистических испытаний Монте-Карло.

система моделирования представляет собой черный ящик который изучается с помощью оценки результатов на реакции на некие импульсы – эксперименты. Результат эксперимента собирается и формируется в некую статистическую совокупность. Он применяется в тех случаях, когда построение аналитической модели явления трудно или вовсе неосуществимо (напр., при решении сложных задач теории массового обслуживания и ряда других задач исследования операций, связанных с изучением случайных процессов). Применение М. М.-К. можно проиллюстрировать примером из области теории очередей. Предположим, надо определить, как часто и как долго придется ждать покупателям в очереди в магазине при заданной его пропускной способности (допустим, для того, чтобы принять решение, следует ли расширять магазин). Подход покупателей носит случайный характер, распределение времени подхода (так можно назвать промежуток времени между каждыми двумя приходами покупателей) может быть установлено из имеющейся информации. Время обслуживания покупателей тоже носит случайный характер, и его распределение тоже может быть выявлено. Таким образом, имеются два стохастических или случайных процесса, взаимодействие которых и создает очередь.

Источник

3.2. Виды экономико-математических моделей в области организации, планирования и управления строительством

Модели, используемые при решении задач организации, планирования и управления строительным производством, условно можно разделить на модели линейного программирования, нелинейные модели, модели динамического программирования, оптимизационные модели, модели управления запасами, целочисленные модели, цифровое моделирование, имитационные модели, вероятностно-статистические модели, модели теории игр, модели итеративного агрегирования, организационно-технологические модели, графические модели, сетевые модели. Рассмотрим каждую из них в отдельности.

3.2.1. Модели линейного программирования

Понятие линейности связано с понятиями пропорциональности и аддитивности (аддитивность — возможность суммирования результатов). Методами математического программирования решаются задачи на экстремум (максимум, минимум) функций многих переменных с ограничениями на область изменения этих переменных. Из методов математического программирования наибольшее распространение получил метод линейного программирования. Слово программирование показывает, что они применяются для планирования, т.е. для составления плана (программы), который обеспечивал бы оптимальное использование материальных и трудовых ресурсов. Слово линейное определяет математическую природу этих моделей. Она состоит в том, что условия задач выражаются системой линейных уравнений или неравенств, содержащих неизвестные только первой степени.

Для любых задач линейного программирования характерны три следующих условия (по академику В.С.Немчинову):

— наличие системы взаимосвязанных факторов;

— строгое определение критерия оценки оптимальности;

— точная формулировка условий, ограничивающих использование

наличных ресурсов. С учетом этих условий экономическим содержанием задач линейного программирования является отыскание наилучших способов использования имеющихся ресурсов, например, определение оптимального плана закрепления потребителей однородного груза за поставщиками. Такого рода задачи получили название транспортных задач линейного программирования. Если нужно использовать разнородные ресурсы, например, различные машины, материалы и т.д. для выполнения какой-либо работы, то применяется общий метод линейного программирования, который получил в соответствии со своей математической основой название симплекс-метода, предложенного американским ученым Дж.Данцигом. Рассмотрим существо модели линейного программирования на простейшем примере.

Задача поиска экстремума линейной функции при линейных ограничениях параметров называется линейным программированием (ЛП).

В задачах ЛП требуется найти минимум некоторой линейной функции, вида (1):

(1)

при линейных ограничениях на параметры (2):

(2)

Методами дифференциального исчисления эта задача не решается, т.к. производные от линейных функций — постоянные величины, которые не приравняешь нулю для нахождения экстремума, как это выполняется в методах решения задач оптимизации с помощью производной.

Для решения задач ЛП используют специальные методы. В частности, так называемый симплекс метод.

Если размерность задачи не велика, то она хорошо иллюстрируется графическими методами.

Воспользуемся известным положением ЛП о том, что экстремум линейной функции находится в одной из вершин многогранника в пространстве или многоугольника на плоскости, образованных ограничениями, которые могут быть представлены в виде плоскостей в пространстве или прямыми линиями на плоскости соответственно, поскольку ограничения есть линейные функции (рис.2).

Рис.2. Плоскости в пространстве

Общий вид задачи на плоскости можно представить в виде выражений (3) и (4):

(3)

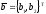
(4)

Цех производит два вида изделий А и В. Их производство ограничено наличием сырья и временем машинной обработки. На изготовление изделия А требуется сырья — 3 кг, а изделия В — 4 кг. Всего сырья в неделю отпускается 1700 кг. Машинного времени требуется на изготовление изделия А — 12 мин., а изделия В — 30 мин. Всего машинного времени в неделю — 160 часов. При этом прибыль от продажи, допустим, изделия А — 2 у.е., изделия В — 4 у.е.

Вопрос: Сколько цеху производить деталей вида А и В, чтобы прибыль была максимальной?

Решение: Разработаем математическую модель.

Пусть х₁ — количество изделий А, выпускаемых в неделю;

х₂ — количество изделий В, выпускаемых в неделю.

Тогда еженедельная прибыль находится по уравнению (5):

(5)

Наша задача обеспечить ее максимум.

Ограничение на сырье и ограничение на машинное время определим уравнениями (6) и (7):

(6)

или (7)

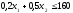
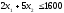
Задача двухмерная, поэтому она может быть легко решена графически.

Нарисуем область определения параметров x₁ и x₂.

Она определяется тремя линиями на плоскости в системе декартовых координат (рис. 3).

Линия № 1 (8) Определяет огранич. на сырье:

(8)

Линия № 2 (9) Огранич. на машинное время:

(9)

Линия № 3 (10) Целевая функция:

(10)

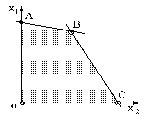
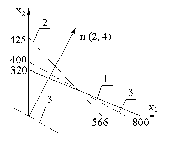
Рис. 3. Область определения параметров

Определим ориентацию градиента целевой функции:

Градиент – это вектор .

Нарисуем вектор параллельный градиенту из начала координат и, используя информацию о том, что экстремум будет в одной из вершин многоугольника определим его.

Он будет в точке В (300, 200).

Заметим, что координату точки экстремума можно определить как точку пересечения двух прямых:

Решая систему, найдем, что x₁ = 300 и x₂ = 200.

По формуле (10.10) находим, что максимальная прибыль составит 1400 у. е.

Источник