Простые модели классификации
Классификация — отнесение объекта к одной из категорий на основании его признаков.
Рассмотрим задачу бинарной классификации. Пусть \( X = \mathbb^d \) — пространство объектов, \( Y = \) — множество допустимых ответов, \( X = <(x_i , y_i )>_^ \) — обучающая выборка. Иногда мы будем класс «+1» называть положительным, а класс «−1» — отрицательным.
Будем считать, что классификатор имеет вид $$ a(x) = \mathrm(b(x)−t) = 2[b(x) > t] − 1. $$
В такого рода задачах возникает необходимость в изучении различных аспектов качества уже обученного классификатора. Сначала обсудим один из подходов к измерению качества таких моделей.
Матрица ошибок
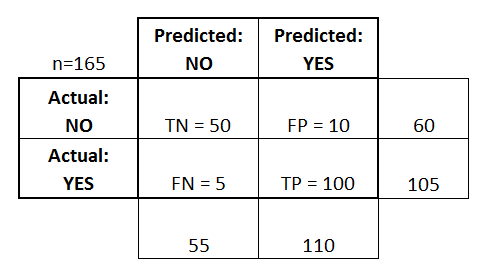
Матрица ошибок — это способ разбить объекты на четыре категории в зависимости от комбинации истинного ответа и ответа алгоритма (см. таблицу ml:class:tbl:2). Через элементы этой матрицы можно, например, выразить долю правильных ответов: $$ \text = \frac <\mathrm
Данная матрика имеет существенный недостаток — её значение необходимо оценивать в контексте баланса классов. Eсли в выборке \( 950 \) отрицательных и \( 50 \) положительных объектов, то при абсолютно случайной классификации мы получим долю правильных ответов \( 0.95 \). Это означает, что доля положительных ответов сама по себе не несет никакой информации о качестве работы алгоритма \( a(x) \), и вместе с ней следует -анализировать соотношение классов в выборке.
Гораздо более информативными критериями являются точность (precision) и полнота (recall).
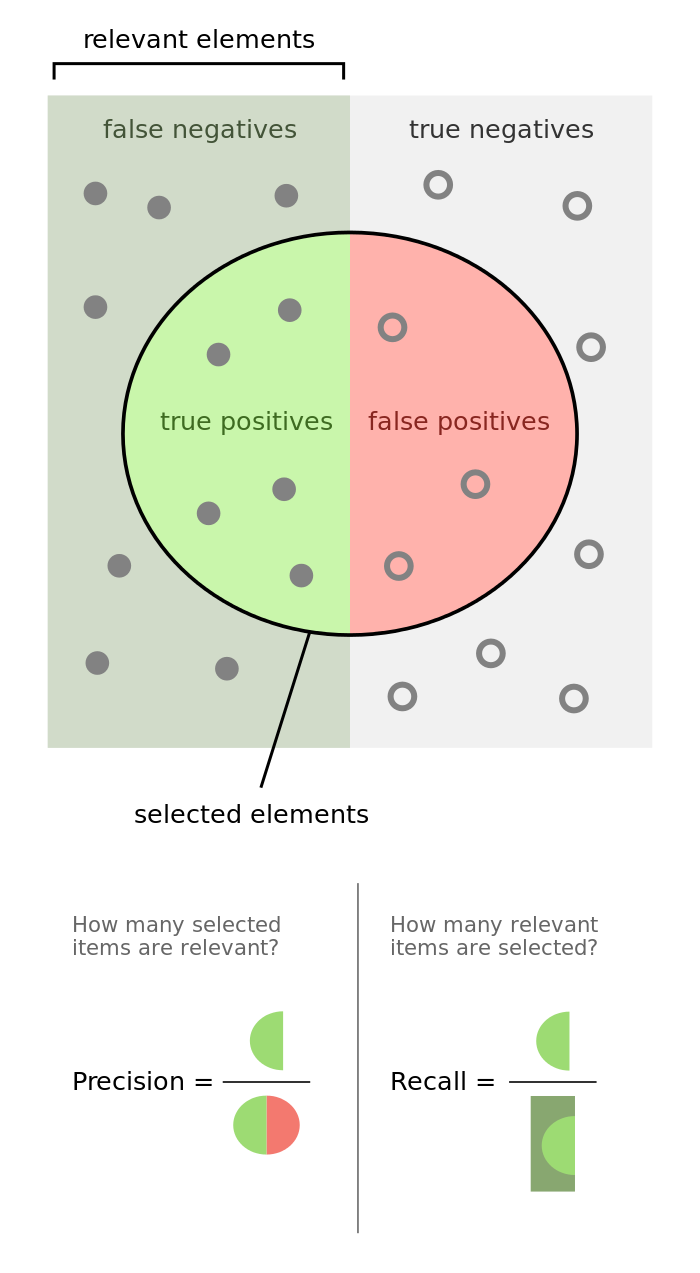
Точность показывает, какая доля объектов, выделенных классификатором как положительные, действительно является положительными: $$ \text = \frac<\mathrm
Полнота показывает, какая часть положительных объектов была выделена классификатором: $$ \text = \frac<\mathrm
Существует несколько способов получить один критерий качества на основе точности и полноты. Один из них — \( F \)-мера, гармоническое среднее точности и полноты: $$ F_\beta = (1+\beta^2) \frac\cdot \text> + \text>. $$
Среднее гармоническое обладает важным свойством — оно близко к нулю, если хотя бы один из аргументов близок к нулю. Именно поэтому оно является более предпочтительным, чем среднее арифметическое (если алгоритм будет относить все объекты к положительному классу, то он будет иметь \( \text = 1 \) и \( \text > 0 \), а их среднее арифметическое будет больше \( 1/2 \), что недопустимо).
Чаще всего берут \( \beta = 1 \) хотя иногда встречаются и другие модификации. \( F_2 \) острее реагирует на recall (т. е. на долю ложноположительных ответов), а \( F_ \) чувствительнее к точности (ослабляет влияние ложноположительных ответов).
В sklearn есть удобная функция sklearn.metrics.classification_report , которая возвращает recall, precision и \( F \)-меру для каждого из классов, а также количество экземпляров каждого класса.
from sklearn.metrics import classification_report y_true = [0, 1, 2, 2, 2] y_pred = [0, 0, 2, 2, 1] target_names = ['class 0', 'class 1', 'class 2'] print(classification_report(y_true, y_pred, target_names=target_names))
Линейная классификация
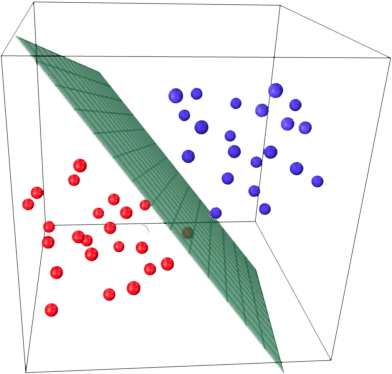
Основная идея линейного классификатора заключается в том, что признаковое пространство может быть разделено гиперплоскостью на две полуплоскости, в каждой из которых прогнозируется одно из двух значений целевого класса. Если это можно сделать без ошибок, то обучающая выборка называется линейно разделимой.
Указанная разделяющая плоскость называется линейным дискриминантом.
Логистическая регрессия
Логистическая регрессия является частным случаем линейного классификатора, но она обладает хорошим «умением» – прогнозировать вероятность отнесения наблюдения к классу. Таким образом, результат логистической регрессии всегда находится на отрезке \( [0, 1] \). Возьмем данные по ирисам
iris = pd.read_csv("https://raw.githubusercontent.com/mwaskom/seaborn-data/master/iris.csv")
sns.pairplot(iris, hue="species")
sns.lmplot(x="petal_length", y="petal_width", data=iris)
X = iris.iloc[:, 2:4].values y = iris['species'].values
from sklearn.preprocessing import LabelEncoder le = LabelEncoder() le.fit(y) y = le.transform(y) y[:5]
iris_pred_names = le.classes_ iris_pred_names
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.3, random_state=0)
from sklearn.preprocessing import StandardScaler sc = StandardScaler() sc.fit(X_train) X_train_std = sc.transform(X_train) X_test_std = sc.transform(X_test)
from sklearn.linear_model import LogisticRegression lr = LogisticRegression(C=100.0, random_state=1) lr.fit(X_train_std, y_train)
lr.predict_proba(X_test_std[:3, :])
lr.predict_proba(X_test_std[:3, :]).sum(axis=1)
lr.predict_proba(X_test_std[:3, :]).argmax(axis=1)
Предсказываем класс первого наблюдения
lr.predict(X_test_std[0, :].reshape(1, -1))
На основе его коэффициентов:
y_pred = lr.predict(X_test_std)
print(classification_report(y_test, y_pred, target_names=iris_pred_names))
Модели классификации в Python
Классификация – отнесение объекта к одной из категорий на основании его признаков.
Метрики качества классификаторов
Матрица ошибок (Confusion matrix)
Матрица ошибок — это способ разбить объекты на четыре категории в зависимости от комбинации истинного ответа и ответа алгоритма.
- T P TP TP — истино-положительное решение;
- T N TN TN — истино-отрицательное решение;
- F P FP FP — ложно-положительное решение (Ошибка первого рода);
- F N FN FN — ложно-отрицательное решение (Ошибка второго рода).
Accuracy — доля правильных ответов:
A c c u r a c y = T P + T N P + N = T P + T N T P + T N + F P + F N = +\mathrm >>= +\mathrm > <\mathrm
Данная матрика имеет существенный недостаток — её значение необходимо оценивать в контексте баланса классов. Eсли в выборке 950 отрицательных и 50 положительных объектов, то при абсолютно случайной классификации мы получим долю правильных ответов 0.95. Это означает, что доля положительных ответов сама по себе не несет никакой информации о качестве работы алгоритма a(x), и вместе с ней следует анализировать соотношение классов в выборке.
Гораздо более информативными критериями являются точность (precision) и полнота (recall).
Точность показывает, какая доля объектов, выделенных классификатором как положительные, действительно является положительными: P r e c i s i o n = T P T P + F P Precision = \frac P rec i s i o n = TP + FP TP
Полнота показывает, какая часть положительных объектов была выделена классификатором: R e c a l l = T P T P + F N Recall = \frac R ec a ll = TP + FN TP
Существует несколько способов получить один критерий качества на основе точности и полноты. Один из них — F-мера, гармоническое среднее точности и полноты: F_\beta = (1 + \beta^2) \cdot \frac <\mathrm
Среднее гармоническое обладает важным свойством — оно близко к нулю, если хотя бы один из аргументов близок к нулю. Именно поэтому оно является более предпочтительным, чем среднее арифметическое (если алгоритм будет относить все объекты к положительному классу, то он будет иметь recall = 1 и precision больше 0, а их среднее арифметическое будет больше 1/2, что недопустимо).
Чаще всего берут β = 1 \beta=1 β = 1 , хотя иногда встречаются и другие модификации. F 2 F_2 F 2 острее реагирует на recall (т. е. на долю ложноположительных ответов), а F 0.5 F_ F 0.5 чувствительнее к точности (ослабляет влияние ложноположительных ответов).
В sklearn есть удобная функция sklearn.metrics.classification_report, возвращающая recall, precision и F-меру для каждого из классов, а также количество экземпляров каждого класса.
import pandas as pd import seaborn as sns from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler, LabelEncoder from sklearn.linear_model import LogisticRegression from sklearn.svm import SVC from sklearn import datasets import numpy as np import matplotlib.pyplot as plt import seaborn as sns %matplotlib inline %config InlineBackend.figure_format = 'svg'
from sklearn.metrics import classification_report y_true = [0, 1, 2, 2, 2] y_pred = [0, 0, 2, 2, 1] target_names = ['class 0', 'class 1', 'class 2'] print(classification_report(y_true, y_pred, target_names=target_names))
precision recall f1-score support
class 0 0.50 1.00 0.67 1
class 1 0.00 0.00 0.00 1
class 2 1.00 0.67 0.80 3
micro avg 0.60 0.60 0.60 5
macro avg 0.50 0.56 0.49 5
weighted avg 0.70 0.60 0.61 5
Линейная классификация
Основная идея линейного классификатора заключается в том, что признаковое пространство может быть разделено гиперплоскостью на две полуплоскости, в каждой из которых прогнозируется одно из двух значений целевого класса. Если это можно сделать без ошибок, то обучающая выборка называется линейно разделимой.
Указанная разделяющая плоскость называется линейным дискриминантом.
Логистическая регрессия
Логистическая регрессия является частным случаем линейного классификатора, но она обладает хорошим «умением» – прогнозировать вероятность отнесения наблюдения к классу. Таким образом, результат логистической регрессии всегда находится в интервале [0, 1].