scipy.optimize.curve_fit#
scipy.optimize. curve_fit ( f , xdata , ydata , p0 = None , sigma = None , absolute_sigma = False , check_finite = None , bounds = (-inf, inf) , method = None , jac = None , * , full_output = False , nan_policy = None , ** kwargs ) [source] #
Use non-linear least squares to fit a function, f, to data.
Assumes ydata = f(xdata, *params) + eps .
Parameters : f callable
The model function, f(x, …). It must take the independent variable as the first argument and the parameters to fit as separate remaining arguments.
xdata array_like
The independent variable where the data is measured. Should usually be an M-length sequence or an (k,M)-shaped array for functions with k predictors, and each element should be float convertible if it is an array like object.
ydata array_like
The dependent data, a length M array — nominally f(xdata, . ) .
p0 array_like, optional
Initial guess for the parameters (length N). If None, then the initial values will all be 1 (if the number of parameters for the function can be determined using introspection, otherwise a ValueError is raised).
sigma None or M-length sequence or MxM array, optional
Determines the uncertainty in ydata. If we define residuals as r = ydata — f(xdata, *popt) , then the interpretation of sigma depends on its number of dimensions:
- A 1-D sigma should contain values of standard deviations of errors in ydata. In this case, the optimized function is chisq = sum((r / sigma) ** 2) .
- A 2-D sigma should contain the covariance matrix of errors in ydata. In this case, the optimized function is chisq = r.T @ inv(sigma) @ r .
None (default) is equivalent of 1-D sigma filled with ones.
absolute_sigma bool, optional
If True, sigma is used in an absolute sense and the estimated parameter covariance pcov reflects these absolute values.
If False (default), only the relative magnitudes of the sigma values matter. The returned parameter covariance matrix pcov is based on scaling sigma by a constant factor. This constant is set by demanding that the reduced chisq for the optimal parameters popt when using the scaled sigma equals unity. In other words, sigma is scaled to match the sample variance of the residuals after the fit. Default is False. Mathematically, pcov(absolute_sigma=False) = pcov(absolute_sigma=True) * chisq(popt)/(M-N)
check_finite bool, optional
If True, check that the input arrays do not contain nans of infs, and raise a ValueError if they do. Setting this parameter to False may silently produce nonsensical results if the input arrays do contain nans. Default is True if nan_policy is not specified explicitly and False otherwise.
bounds 2-tuple of array_like or Bounds , optional
Lower and upper bounds on parameters. Defaults to no bounds. There are two ways to specify the bounds:
- Instance of Bounds class.
- 2-tuple of array_like: Each element of the tuple must be either an array with the length equal to the number of parameters, or a scalar (in which case the bound is taken to be the same for all parameters). Use np.inf with an appropriate sign to disable bounds on all or some parameters.
Method to use for optimization. See least_squares for more details. Default is ‘lm’ for unconstrained problems and ‘trf’ if bounds are provided. The method ‘lm’ won’t work when the number of observations is less than the number of variables, use ‘trf’ or ‘dogbox’ in this case.
Function with signature jac(x, . ) which computes the Jacobian matrix of the model function with respect to parameters as a dense array_like structure. It will be scaled according to provided sigma. If None (default), the Jacobian will be estimated numerically. String keywords for ‘trf’ and ‘dogbox’ methods can be used to select a finite difference scheme, see least_squares .
If True, this function returns additioal information: infodict, mesg, and ier.
Defines how to handle when input contains nan. The following options are available (default is None):
- ‘raise’: throws an error
- ‘omit’: performs the calculations ignoring nan values
- None: no special handling of NaNs is performed (except what is done by check_finite); the behavior when NaNs are present is implementation-dependent and may change.
Note that if this value is specified explicitly (not None), check_finite will be set as False.
Keyword arguments passed to leastsq for method=’lm’ or least_squares otherwise.
Returns : popt array
Optimal values for the parameters so that the sum of the squared residuals of f(xdata, *popt) — ydata is minimized.
pcov 2-D array
The estimated approximate covariance of popt. The diagonals provide the variance of the parameter estimate. To compute one standard deviation errors on the parameters, use perr = np.sqrt(np.diag(pcov)) . Note that the relationship between cov and parameter error estimates is derived based on a linear approximation to the model function around the optimum [1]. When this approximation becomes inaccurate, cov may not provide an accurate measure of uncertainty.
How the sigma parameter affects the estimated covariance depends on absolute_sigma argument, as described above.
If the Jacobian matrix at the solution doesn’t have a full rank, then ‘lm’ method returns a matrix filled with np.inf , on the other hand ‘trf’ and ‘dogbox’ methods use Moore-Penrose pseudoinverse to compute the covariance matrix. Covariance matrices with large condition numbers (e.g. computed with numpy.linalg.cond ) may indicate that results are unreliable.
infodict dict (returned only if full_output is True)
a dictionary of optional outputs with the keys:
The number of function calls. Methods ‘trf’ and ‘dogbox’ do not count function calls for numerical Jacobian approximation, as opposed to ‘lm’ method.
The residual values evaluated at the solution, for a 1-D sigma this is (f(x, *popt) — ydata)/sigma .
A permutation of the R matrix of a QR factorization of the final approximate Jacobian matrix, stored column wise. Together with ipvt, the covariance of the estimate can be approximated. Method ‘lm’ only provides this information.
An integer array of length N which defines a permutation matrix, p, such that fjac*p = q*r, where r is upper triangular with diagonal elements of nonincreasing magnitude. Column j of p is column ipvt(j) of the identity matrix. Method ‘lm’ only provides this information.
The vector (transpose(q) * fvec). Method ‘lm’ only provides this information.
A string message giving information about the solution.
An integer flag. If it is equal to 1, 2, 3 or 4, the solution was found. Otherwise, the solution was not found. In either case, the optional output variable mesg gives more information.
if either ydata or xdata contain NaNs, or if incompatible options are used.
if the least-squares minimization fails.
if covariance of the parameters can not be estimated.
Minimize the sum of squares of nonlinear functions.
Calculate a linear least squares regression for two sets of measurements.
Users should ensure that inputs xdata, ydata, and the output of f are float64 , or else the optimization may return incorrect results.
With method=’lm’ , the algorithm uses the Levenberg-Marquardt algorithm through leastsq . Note that this algorithm can only deal with unconstrained problems.
Box constraints can be handled by methods ‘trf’ and ‘dogbox’. Refer to the docstring of least_squares for more information.
[1] K. Vugrin et al. Confidence region estimation techniques for nonlinearregression in groundwater flow: Three case studies. Water Resources Research, Vol. 43, W03423, DOI:10.1029/2005WR004804
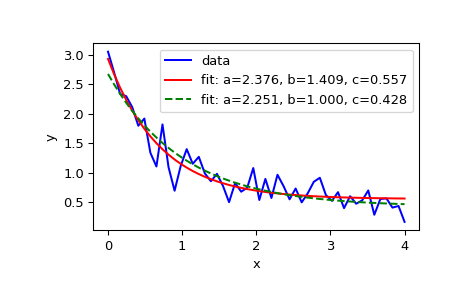
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy.optimize import curve_fit
>>> def func(x, a, b, c): . return a * np.exp(-b * x) + c
Define the data to be fit with some noise:
>>> xdata = np.linspace(0, 4, 50) >>> y = func(xdata, 2.5, 1.3, 0.5) >>> rng = np.random.default_rng() >>> y_noise = 0.2 * rng.normal(size=xdata.size) >>> ydata = y + y_noise >>> plt.plot(xdata, ydata, 'b-', label='data')
Fit for the parameters a, b, c of the function func:
>>> popt, pcov = curve_fit(func, xdata, ydata) >>> popt array([2.56274217, 1.37268521, 0.47427475]) >>> plt.plot(xdata, func(xdata, *popt), 'r-', . label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))
Constrain the optimization to the region of 0
>>> popt, pcov = curve_fit(func, xdata, ydata, bounds=(0, [3., 1., 0.5])) >>> popt array([2.43736712, 1. , 0.34463856]) >>> plt.plot(xdata, func(xdata, *popt), 'g--', . label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))
>>> plt.xlabel('x') >>> plt.ylabel('y') >>> plt.legend() >>> plt.show()
For reliable results, the model func should not be overparametrized; redundant parameters can cause unreliable covariance matrices and, in some cases, poorer quality fits. As a quick check of whether the model may be overparameterized, calculate the condition number of the covariance matrix:
>>> np.linalg.cond(pcov) 34.571092161547405 # may vary
The value is small, so it does not raise much concern. If, however, we were to add a fourth parameter d to func with the same effect as a :
>>> def func(x, a, b, c, d): . return a * d * np.exp(-b * x) + c # a and d are redundant >>> popt, pcov = curve_fit(func, xdata, ydata) >>> np.linalg.cond(pcov) 1.13250718925596e+32 # may vary
Such a large value is cause for concern. The diagonal elements of the covariance matrix, which is related to uncertainty of the fit, gives more information:
>>> np.diag(pcov) array([1.48814742e+29, 3.78596560e-02, 5.39253738e-03, 2.76417220e+28]) # may vary
Note that the first and last terms are much larger than the other elements, suggesting that the optimal values of these parameters are ambiguous and that only one of these parameters is needed in the model.