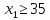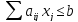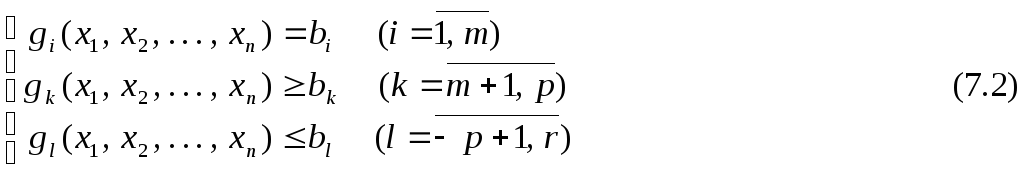Компоненты задачи математического программирования

1. Определение задачи математического программирования

Математическое программирование — это область математики, разрабатывающая теорию, решения многомерных задач с ограничениями. В отличие от классической математики, мы находим наилучший вариант из всех возможных.

Итак, математическое программирование — это раздел высшей математики, занимающийся решением задач, связанных с нахождением экстремумов функций нескольких переменных при наличии ограничений на переменные.

Общая задача М. п. состоит в нахождении оптимального (максимального или минимального) значения целевой функции, причем значения переменных должны принадлежать некоторой области допустимых значений.

Классическая задача математического программирования – задача выбора таких значений некоторых переменных, подчиненных системе ограничений в форме равенств, при которых достигается max или min функции.

2. Допустимое решение задачи, одр, оптимальное решение задачи.

Допустимым решением задачи называется любой n-мерный вектор

x (x = (,,…,)), удовлетворяющий системе ограничений и условию неотрицательности.

Множество допустимых решений образует ОДР.

Оптимальным решением задачи называется такое допустимое решение, при котором целевая функция достигает экстремума.

3. Экономико–математические модели задач лп: задача о банке

К экономико-математическим моделям задач ЛП относятся:Задача планирования производства, определения оптимального ассортимента продукции, о диете, о банке, составления жидких смесей, Транспортная задача

Построение экономико – математической модели.

Задача о банке

Собственные средства банка в сумме с депозитами составляют 100 млн. $. Не менее 35 млн. $ из этой суммы размещена в кредитах (не ликвид). Ликвидное ограничение ценных бумаг должны составлять не менее 30 %, размещенных в кредитах и ликвидных активах.

Пусть 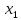— средства, размещенные в кредитах,– средства, размещенные в ликвидных активах.

Банк. Огран. (1)

Кред. Огран.

Ликвид. Огран.

Условие неопределенности ,≥0 (4)

— доходность кредитов, — доходность ликвидных активов

F = при услов. (1) – (4).

4. Экономико – математические модели задач лп: задача определения оптимального ассортимента продукции.

— П1, — П2

F = 3

2

3

5. Задача лп, стандартная форма, каноническая форма.

К математическим задачам линейного программирования относят исследования конкретных производственно-хозяйственных ситуаций, которые в том или ином виде интерпретируются как задачи об оптимальном использовании ограниченных ресурсов.

Задачей линейного программирования является выбор из множества допустимых планов наиболее выгодного (оптимального).

Экономико-математическая модель любой задачи линейного программирования включает: целевую функцию, оптимальное значение которой (максимум или минимум) требуется отыскать; ограничения в виде системы линейных уравнений или неравенств; требование неотрицательности переменных.

В общем виде модель записывается следующим образом:

Целевая функция: F (x)= c1x1 + c2x2 + . + cnxn → max(min)

ограничения: a11x1 + a12x2 + . + a1nxn b1,

требование неотрицательности: xj ≥ 0,

Задача имеет каноническую форму, если является задачей на максимум (минимум) линейной функции F и ее система ограничений состоит только из равенств (уравнений). При этом переменные задачи х1, х2, . хn являются неотрицательными:

F (x) =

, i= 1,2…m

, j = 1,2…n

В стандартной форме задача линейного программирования является задачей на максимум (минимум) линейной функции f и система ограничений ее состоит из одних линейных неравенств типа «

F (x) =

, i= 1,2…m

, j = 1,2…n

Допустимое множество решений задачи ЛП либо пусто, либо является выпуклым многогранником (как пересечение полупространств, описываемых ограничениями-неравенствами). Оно может быть как ограниченным, так и неограниченным; в любом случае это замкнутый многогранник.

Если допустимое множество не пусто, а целевая функция ограничена сверху (для задачи максимизации, а для задачи минимизации — ограничена снизу) на этом множестве, то задача ЛП имеет оптимальное решение.

Оптимальные решения задачи ЛП (если они существуют) всегда находятся на границе допустимого множества. Точнее, если существует единственное оптимальное решение, то им является какая-либо вершина многогранника допустимых решений; если две или несколько вершин являются оптимальными решениями, то любая их выпуклая комбинация также является оптимальным решением (т.е. существует бесконечно много точек максимума или минимума)

Источник

7. Общая постановка и разновидности задач математического программирования

Математическое программирование — обширная область знаний. Мы рассмотрели далеко не полностью один из разделов — линейное программирование.

Общая математическая схема задачи математического программирования такова: дана некоторая функция

и некоторая система ограничений , наложенных на переменные x₁, x₂, . . . , x_n:

Требуется найти такой набор значений переменных x₁, x₂, . . . , x_n, который удовлетворяет ограничениям (7.2), и при этом условии минимизирует или максимизирует функцию (7.1).

Если все фигурирующие в (7.1) и (7.2) функции линейны, то мы имеем ЗЛП. В противном случае получается задача нелинейного программирования.

Для задач нелинейного программирования нет такого универсального метода решения, каким является симплекс-метод для ЗЛП. Только для узких классов задач нелинейного программирования разработаны точные методы, основная масса решается приближенно.

В некоторых задачах математического программирования ОДР состоит из дискретного множества точек. Такие задачи называются дискретными оптимизационными задачами. Например, если в ЗЛП потребовать, чтобы переменные принимали только целые значения, то получится дискретная оптимизационная задача — задача целочисленно­го линейного программирования. Дискретные задачи, как правило, сложнее непрерывных. По задачам дискретной оптимизации в настоящее время проводятся интенсивные научные исследования.

Важной областью является и динамическое программирование. Здесь изучаются методы поэтапного решения оптимизационных задач. Такие методы используются в особенно сложных задачах. Например, при составлении плана работы завода на год целесообразно разбить год на месяцы и план работы на каждый месяц увязывать с планами на предыдущие и последующие месяцы.

Наконец отметим, что встречаются задачи математического программирования, в которых исходные данные являются случайными величинами. Такие задачи изучает стохастическое программирование. Стохастическое программирование использует теоретико-вероятностные, статистические и оптимизационные методы.

По математическому программированию написано уже много книг. Приводимая литература — незначительная часть их. Но в ней можно найти изложение основных положений математического программирования, а также ссылки на другие источники.

Литература

1. Крушевский А.В., Швецов К.М. Математическое программирование и моделирование в экономике.-К.: Вища шк., 1979

2. Кузнецов Ю.Н., Кузубов В.М., Волощенко А.Б. Математическое программирование.-М.: Высш.шк.,1980

3. Таха X. Введение в исследование операций. (В 2-х книгах).- М.:Мир,1985

4. Мину М. Математическое программирование. Теория и алгоритмы.-М.: Наука, 1990.

Источник