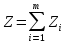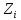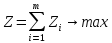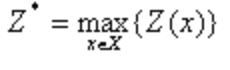Тема 2.3 Динамическое программирование
Динамическое программирование – раздел оптимального программирования (оптимального управления), в котором процесс принятия решения и управления, может быть разбит на отдельные этапы (шаги). Все шаги могут быть уникальными или одинаковыми и чередоваться друг с другом. Некоторые задачи оптимизации легко разделяются на шаги естественным способом, а для других вводится искусственное разделение на шаги.
Динамическое программирование позволяет свести одну сложную задачу со многими переменными ко многим задачам с малым числом переменных. Это значительно сокращает объем вычислений и ускоряет процесс принятия управленческого решения.
Экономический процесс является управляемым, если можно влиять на ход его развития.
Управление – совокупность решений, принимаемых на каждом этапе для влияния на ход развития процесса.
Операция – управляемый процесс, т.е. мы можем выбирать какие-то параметры, влияющие на ход процесса и управлять шагами операции, обеспечивать выигрыши на каждом шаге и в целом за операцию.
Решение на каждом шаге называется «шаговым управлением». Совокупность всех шаговых управлений представляет собой управление операцией в целом.
Примерами задач, решаемых методом динамического программирования, могут быть: распределение ресурсов (финансовых, сырьевых, материальных и т.д.) между предприятиями, замена или ремонт промышленного оборудования, прокладка коммуникаций (трубопроводов, дорог и т.д.) и пр. В этих задачах, как правило, в качестве шагов выступают отрезки времени, которые явно задаются в условии задачи.
Требуется найти такое управление (х), при котором выигрыш обращался бы в максимум:
где F– выигрыш за операцию;
Fi(xi) – выигрыш наi-мшаге;
х – управление операцией в целом;
хi– управление наi-мшаге(i=1,2,…,m).В общем случае шаговые управления(х1, х2, … хm)могут стать числами, векторами, функциями.
То управление (х*), при котором достигается максимум, называется оптимальным управлением. Оптимальность управления состоит из совокупности оптимальных шаговых управленийх* = х*1, х*2, … х*m
F* = max –максимальный выигрыш, который достигается при оптимальном управлении х*.
Исходя из условий, каждой конкретной задачи длину шага выбирают таким образом, чтобы на каждом шаге получить простую задачу оптимизации и обеспечить требуемую точность вычислений.
Нахождение кратчайшего пути
Выбор оптимального решения на конкретном шаге не дает гарантии получения оптимального решения всей задачи. Поэтому для получения оптимального решения в задаче иногда приходится выбирать не лучшее решение на конкретном шаге. Планирование многошаговой задачи сводится к выбору такого решения на каждом шаге, которое учитывает последствие на следующих шагах. На текущем шаге выбирается не лучшее решение, а то, которое предполагает максимальную сумму выигрыша от всех оставшихся шагов. Поэтому выполнять вычисления в задачах ДП удобнее от конца к началу. Выполняя вычисление по последнему шагу, делается ряд предположений, как закончился предыдущий шаг и для каждого предположения найти условно оптимальное решение до первого шага. Т.о. будут найдены условно-оптимальные решения на каждом шаге. Далее выполняется переход от условно-оптимального к безусловно-оптимальному решению. Вычисления идут от первого шага к последнему, используя полученные условно-оптимальные решения.
Распределение ресурсов
Общий подход к решению задач распределения ресурсов тот же, но имеют некоторые особенности. Распределить некоторый ресурс, например, финансы в объеме Sмежду предприятиямиP1,P2,Pn. Вложение в каждое предприятие должно приносить дополнительную прибыль. Чем больше сумма финансовых вложений в предприятие, тем больше дополнительный доход. Но может быть так, что начиная с какого-то момента, дополнительная прибыль не увеличивается, т. е. предприятие не может освоить выделенные ресурсы.
Задача распределения ресурсов стоит так: как распределить выделенные ресурсы между предприятиями, чтобы суммарный доход от всех предприятий был максимальным. Распределяемые ресурсы выделяются порциями, распределенные во времени. Перед каждым шагом имеется некоторая сумма Sеще не распределенных ресурсов. На каждом шаге предприятиям назначаются ресурсыx1,x2,xn. Требуется найти оптимальное сочетаниеx1,x2,xn, при котором совокупный доход максимален.
Оптимизацию начинаем с последнего шага m. На этом шаге остаток ресурсовS. Их нужно назначить последнему предприятиюPn. Оптимальное решение будет выглядитxn(S)=S. Условно-оптимальный доход составитLm(S)=αm(S). На предпоследнем шагеn-1 запас ресурсовS, а условно-оптимальный доход на двух последних шагах,Ln-1(S)Если на предпоследнем шаге будут выделены ресурсыx, то на последнем шаге ресурсов останетсяS-xи условно—оптимальный жоход на двух последних шагах составитLn-1(S)=αn-1(S)+Ln(S-x) и нужно найти такойx, чтобы доход был максимальным.
Дойдя до первого шага будем иметь начальное значение ресурсов Q, поэтому условно-оптимальный доход составит:L=max1(x)+L2(Q—x)>. Далее выполнить обратное вычисление и уточнить распределение ресурсов.
Принцип оптимальности Беллмана
Основным методом динамического программирования является метод рекуррентных соотношений; который основывается на использовании принципа оптимальности, разработанного американским математиком Р.Беллманом.
Каковы бы ни были начальное состояние на любом шаге и управление, выбранное на этом шаге, последующие управления должны выбираться ОПТИМАЛЬНЫМИ относительно состояния, к которому придет система в конце каждого шага.
Использование данного принципа гарантирует, что управление, выбранное на любом шаге, не локально лучше, а лучше с точки зрения процесса в целом.
Условная оптимизация
Безусловная оптимизация
Si – состояние системы наi-мшаге. Основная рекуррентная формула динамического программирования в случае решения задачи максимизации имеет вид:
, где максимум в данной формуле берется по всем возможным решениям в ситуации, когда система на шаге mнаходится в состоянииi.
Величина fm(i)– есть максимальная прибыль завершения задачи из состоянияi, если предположить, что на шагеm, система находится в состоянииi.
Максимальная прибыль может быть получена максимизацией суммы прибылей самого шага m и максимальной прибыли шага(m+1) и далее, чтобы дойти до конца задачи.
Планируя многошаговую операцию надо выбирать управление на каждом шаге с учетом всех его будущих последствий на ещё предстоящих шагах.
Управление на i-м шаге выбирается не так, чтобы выигрыш именно на данном шаге был максимальным, а так, чтобы была максимальна сумма выигрышей на всех оставшихся шагах плюс данный шаг.
Среди всех шагов последний шаг планируется без оглядки на будущее, т.е. чтобы он сам, как таковой принес наибольшую выгоду.
Задача динамического программирования решается в два этапа:
1 этап (от конца к началу по шагам):Проводится условная оптимизация, в результате чего находится условные оптимальные управления и условные оптимальные выигрыши по всем шагам процесса.
2 этап (от начала к концу по шагам):Выбираются (просчитываются) уже готовые рекомендации от 1-го шага до последнего и находитсябезусловное оптимальное управлениех*, равныйх*1, х*2, …, х*m.
Пример. Имеется запас средств, который нужно распределить между предприятиями, чтобы получить наибольшую прибыль. Пусть начальный капитал S0=100 д.ед. Функции дохода предприятий даны в матрице прибылей по каждому предприятию.
7. Основные понятия динамического программирования. Задачи, приводящие к динамическому программированию.
Динамическое программирование — это способ решения сложных задач путём разбиения их на более простые подзадачи.
Ключевая идея в динамическом программировании достаточно проста. Как правило, чтобы решить поставленную задачу, требуется решить отдельные части задачи (подзадачи), после чего объединить решения подзадач в одно общее решение. Часто многие из этих подзадач одинаковы. Подход динамического программирования состоит в том, чтобы решить каждую подзадачу только один раз, сократив тем самым количество вычислений.
Для определения сущности динамического программирования представим себе некоторую операцию О, состоящую из ряда последовательных «шагов» или этапов, например, деятельность отрасли промышленности в течение m хозяйственных лет. Выигрыш (эффективность операции) Z за всю операцию складывается из выигрышей на отдельных шагах:
где – выигрыш на i-м шаге.
Если Z обладает таким свойством, то его называют аддитивным критерием.
Операция О является управляемым процессом, то есть мы можем выбирать какие-то параметры, которые влияют на его ход и исход, причем на каждом шаге выбирается решение, от которого зависит выигрыш и на данном шаге, и выигрыш за операцию в целом. Эти решения называются шаговыми.
Совокупность всех шаговых решений является управлением операцией в целом. Обозначим его буквой х, а шаговые управления – буквами х1, х2, . , хm:
Требуется найти такое управление х, при котором выигрыш Z обращается в максимум:
Управление х*, при котором этот максимум достигается, называется оптимальным управлением. Оно состоит из совокупности оптимальных шаговых управлений: х*=х*(х1*, х2*, . , хm*).
Максимальный выигрыш, который достигается при этом управлении, обозначим следующим образом:
где Х– множество допустимых (возможных) управлений.
Самый простой способ решения задачи – полный перебор всех вариантов. Когда количество вариантов невелико, этот способ вполне приемлем. Однако на практике задачи с небольшим числом вариантов встречаются весьма редко, поэтому полный перебор, как правило, неприемлем из-за чрезмерных затрат вычислительных ресурсов. Поэтому в таких случаях на помощь приходит динамическое программирование.
В идее динамического программирования есть принципиальная тонкость: каждый шаг оптимизируется не сам по себе, а с «оглядкой на будущее», на последствия принимаемого «шагового» решения. Оно должно обеспечить максимальный выигрыш не на данном конкретном шаге, а на всей совокупности шагов, входящих в операцию.
Метод динамического програмирования может применяться только для определенного класса задач. Эти задачи должны удовлетворять таким требованиям:
- Задача оптимизации интерпретируется как n-шаговый процесс управления.
- Целевая функция равна сумме целевых функций каждого шага.
- Выбор управления на k-м шаге зависит только от состояния системы к этому шагу и не влияет на предшествующие шаги (нет обратной связи).
- Состояние системы sk после k-го шага управления зависит только от предшествующего состояния sk-1 и управления xk (отсутствие последействия).
- На каждом шаге управление xk зависит от конечного числа управляющих переменных, а состояние sk – от конечного числа параметров.