Классификация методов линейного программирования

Классификация методов решения задач целочисленного линейного программирования

Целочисленное линейное программирование (ЦЛП) — раздел математического программирования, ориентированный на решение задач, в которых на все или на некоторые переменные наложено требование целочисленности. В соответствии с этим определением все задачи ЦЛП подразделяются на полностью целочисленные и частично целочисленные. В полностью целочисленных задачах требование целочисленности накладывается на все переменные, а в частично целочисленных задачах — только на часть переменных.

Основные трудности решения задач ЦЛП связаны с эффектом округления чисел, возникающим при использовании ЭВТ. Округление чисел неприемлемо для получения решения задачи ЦЛП по следующим причинам:

• 1) решение в результате округления может быть получено в точке, не являющейся на самом деле оптимальной. Например, если значение одной из базисных переменных в оптимальном решении равно 10,1, то округление ее до 10 может привести к недопустимости решения, т. е. к выходу из области допустимых решений;
• 2) округление не имеет смысла в том случае, если переменные задачи ЦЛП — булевы, т. е. могут принимать только два значения: 0 или 1;
• 3) округление невозможно в том случае, если в задаче речь идет о неделимых объектах, например о предприятиях, наручных часах, людях и т. д.

Существуют следующие методы решения задач ЦЛП:

• 1. Методы отсечений. К этой группе методов относятся методы отсекающих плоскостей Гомори, которые разработаны для решения как частично, так и полностью целочисленных задач. Существо метода состоит в следующем: сначала решается задача ЦЛП как задача линейного программирования без учета требования целочисленности, а затем вводятся дополнительные ограничения, которые отсекают от области допустимых решений части плоскости, не содержащие целочисленных значений переменных.
• 2. Комбинаторные методы. К этой группе методов относится метод ветвей и границ. Существо метода заключается в переборе всех допустимых целочисленных решений. Основная трудность реализации метода состоит в формировании множества приемлемой мощности допустимых целочисленных решений.
• 3. Комбинированные методы. Эти методы используются только тогда, когда целочисленные переменные являются булевыми. Булевы свойства переменных значительно упрощают процесс решения задачи ЦЛП, поэтому существуют специальные процедуры приведения таких задач к виду, где целочисленные переменные преобразуются в булевые. К этой группе методов может быть отнесен метод частичного перебора.

Источник

Классификация методов оптимизации

Линейное программирование — раздел математики, в котором изучаются методы решения задач на отыскание экстремумов (максимума, минимума) линейной функции при наличии ограничений в виде линейных уравнений или линейных неравенств.

2.1 Общая задача линейного программирования (злп)

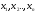
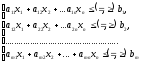
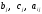
Найти решение X(), при котором функция (2.1) достигает экстремума – максимума (минимума) при выполнении условий (2.2) (2.3) Значения предполагаются известными (выявлены на стадии анализа реальной ситуации). Линейная функция (2.1) называется целевой функцией (линейной формой), х₁, х₂. х_n— аргументами целевой функции. Условия (2.2) называются ограничениями задачи, Условия (2.3) показывают, что аргументы могут быть любого знака. Решение X(), системы (2.2) называется допустимым решением ЗЛП, если числа — неотрицательны. Совокупность всех допустимых решений называется областью допустимых решений задачи (ОДР). Допустимое решение, которое обращает в максимум (минимум) целевую функцию (2.1) называется оптимальным решением ЗЛП.

2.2 Математические модели задач линейного программирования

Рассмотрим некоторые экономические задачи, которые являются задачами линейного программирования. Пример 1. Задача использования сырья Для использования двух ви­дов продукции P₁ и P₂ используется три вида сырья S₁, S₂ и S₃,запасы сырья соответственно равны 40,60,50 единиц сырья. Затраты сырья на изго­товление единицы продукции P₁ соответственно равны 2,8,5. Затраты сырья на изго­товление единицы продукции P₂ соответственно равны 5,3,6. Прибыль от реализации единицы продукции каждого вида соответственно равна 100, 200 у.е. Необходимо составить математическую модель плана выпуска продук­ции, при котором прибыль от реализации изделий будет максимальной. Решение Условие задачи запишем в следующую таблицу:

Вид сырья	Запасы	Затраты сырья на ед. изделий вида
		P1	P2
S1	40	2	5
S2	60	8	3
S3	50	5	6
Прибыль от единицы продукции		100	200

Составим математическую модель задачи: пусть — количество единиц продукцииP₁, — количество единиц продукции P₂, планируемое к выпуску. Тогда целевая функции – суммарная прибыль от реализации изделий имеет вид: . Ограничения по запасам сырья записываются следующими неравенствами: Если продукция P₁ не выпускается, то , а если выпускается, то х₁ > 0, аналогично и для Р₂, следовательно имеют место условия неотрицательности: Таким образом, математическая модель данной задачи линейного программирования имеет вид: Найти оптимальный план производства X(,), такой, что Пример 2. Задача составления рациона (задача «о диете») На животноводческой ферме каждое животное ежедневно должно получать не менее 7 единиц питательного вещества S₁, 9 единиц вещества S₂ и 14 единиц вещества S₂ Для составления рациона используют два вида корма. Содержание количества единиц питательных веществ в 1 кг корма приведены в таблице. Необходимо составить рацион нужной питательности, причем затраты на него должны быть минимальными.

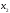
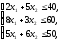
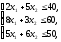
Вещества	Кол-во ед. питательных веществ в кг. корма
	Корм 1	Корм 2
S1	2	5
S2	8	5
S3	5	4
Стоимость 1 кг корма	14	26

Решение Составим математическую модель задачи пусть — количество килограммов корма 1, — количество килограммов корма 2. Ограничения на питательность рациона по трем видам питательных веществ S_1, S₂ , S₃ имеют вид условия неотрицательности : Затраты на питание выражаются целевой функцией:

Источник

Основная задача линейного программирования

Получение оптимального плана-решения в задачах с линейной структурой. Классификация методов линейного программирования. Модель основной задачи линейного программирования в разных формах записи. Графический метод решения задачи линейного программирования.

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Размещено на http://www.allbest.ru/

Линейное программирование. Основная задача линейного программирования

1. Классификация методов линейного программирования

2. Основная задача линейного программирования и её модель в различных формах записи

3. Графический метод решения задачи линейного программирования

линейный задача программирование графический

1. Классификация методов линейного программирования

Большое число экономических задач сводится к линейным математическим моделям. Традиционно оптимизационные линейные математические модели называются моделями линейного программирования. Этот термин появился, когда программирование на компьютере еще не было развито, и соответственно не очень удачному переводу английского «programmation». Линейное программирование возникло в СССР. В конце 30-х годов XX в. советский экономист-математик Леонид Витальевич Канторович открыл класс этих задач и придумал некоторые частные методы их решения. В 1975 г. фактически за это открытие он был удостоен Нобелевской премии по экономике, что уже свидетельствует о большой важности задач линейного программирования.

С чисто математической точки зрения задачи линейного программирования интересны тем, что здесь неприменимы методы нахождения экстремумов с помощью производной.

Под линейным программированием понимается линейное планирование, т.е. получение оптимального плана-решения в задачах с линейной структурой.

Задачами линейного программирования называются задачи, в которых линейны как целевая функция, так и ограничения в виде равенств и неравенств и для которых методы математического анализа оказываются непригодными. Линейное программирование представляет собой наиболее часто используемый метод оптимизации.

Методы линейного программирования подразделяются на группы:

1) группа симплексных методов (точные);

2) группа распределительных методов (точные и приближённые).

Точные — методы перебора вариантов решения задачи в итоге дающие оптимальный вариант. Используются при машинном решении задач.

Приближённые — позволяют получить только один из допустимых вариантов решения задачи. Используются для получения первого варианта в точных распределительных методах или для ручного решения задачи.

Каждая группа методов имеет свою базовую задачу. Для группы симплекс-методов базовой является «Основная задача линейного программирования», для группы распределительных методов — «Транспортная задача».

2. Основная задача линейного программирования и ее модель в различных формах записи

Пусть некоторое предприятие имеет m видов производственных ресурсов. Порядковый номер ресурсов — i, т.е. i=1, 2,…, m.

Наличие каждого вида ресурсов известно и обозначается b_i.

Предположим, что предприятие может производить n видов продукции. Порядковый номер продукции — j, т.е. j=1, 2, …, n.

Необходимо определить какое количество единиц продукции каждого вида надо производить (x_j), чтобы получить максимум этой продукции в стоимостном выражении, если известны затраты на производство единицы продукции каждого вида ресурса (a_ij) и цена реализации (c_j).

Развернутая форма записи модели.

I. Целевая функция — описывает выход продукции в стоимостном выражении:

II. Система основных ограничений — описывает с помощью математической зависимости тот факт, что расходы производственных ресурсов не должны превышать их наличие:

III. Условие неотрицательности переменных величин:

Замечание: в постановке с выбором другого критерия оптимальности целевая функция может стремиться к минимуму. Кроме того система ограничений может быть смешанной, т.е. содержать не только неравенства (,), но и равенства.

Структурная форма записи модели.

В такой форме модели даются в специализированной литературе. В этой форме записи отражается структура и тип ограничений, структура функции, какие переменные входят в функцию Z и в ограничения.

III. x_j0, j=1,2,…,n.

Замечание: одной формулой можно описать ограничения, имеющие одинаковую структуру и тип и включающие в себя одни и те же переменные.

Существуют также векторная, матричная и табличная формы записи модели.

Подобные документы

Сущность линейного программирования. Изучение математических методов решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейной целевой функцией. Нахождение точек наибольшего или наименьшего значения функции.

Общее понятие вектора и векторного пространства, их свойства и дополнительные структуры. Графический метод в решении задачи линейного программирования, его особенности и область применения. Примеры решения экономических задач графическим способом.

История зарождения и создания линейного программирования. Транспортная задача. Общая постановка, цели, задачи. Основные типы, виды моделей. Методы составления начального опорного плана. Понятие потенциала и цикла. Задача, двойственная к транспортной.

Понятие линейного программирования и его основные методы. Формулировка задачи линейного программирования в матричной форме и ее решение различными методами: графическим, табличным, искусственного базиса. Особенности решения данной задачи симплекс-методом.

Задача целочисленного линейного программирования, приведение к канонической форме. Общие идеи методов отсечения. Алгоритм Гомори для решения целочисленных задач линейного программирования. Понятие правильного отсечения и простейший способ его построения.

Источник