Нелинейное программирование Общая постановка задачи
где xj – переменные, — заданные функции от п переменных, bi – фиксированные значения.
Для задачи нелинейного программирования в отличие от линейных задач нет единого метода решения. В зависимости от вида целевой функции и системы ограничений разработаны специальные методы решения, к которым относятся методы множителей Лагранжа, квадратичное и выпуклое программирование, градиентные методы, приближённые методы решения, графический метод.
Графический метод
Рассмотрим примеры решение задач нелинейного программирования с двумя переменными, причём их целевые функции и системы ограничений могут быть заданы в линейном и нелинейном виде. Так же как и в задачах линейного программирования, они могут быть решены графически.
Задача с линейной целевой функцией и нелинейной системой ограничений
Пример 1. Найти глобальные экстремумы функции
ОТВЕТ. Глобальный минимум, равный нулю, достигается в точке О(0, 0), глобальный максимум, равный , — в точке
Задача с нелинейной целевой функцией и линейной системой ограничений
Пример 2. Найти глобальные экстремумы функции
ОТВЕТ. Глобальный максимум, равный 58, достигается в точке D(9, 0), глобальный минимум, равный нулю, — в точке О1(2, 3).
Пример 3. Найти глобальные экстремумы функции
ОТВЕТ. Глобальный максимум, равный 52, находится в точке О(0, 0). Глобальный минимум, равный 1053/169, находится в точке Е(51/13б21/13).
Задача с нелинейной целевой функцией и нелинейной системой ограничений
Пример 4. Найти глобальные экстремумы функции
ОТВЕТ. Глобальный минимум, равный нулю, достигается в точке О1(2, 1), глобальный максимум, равный 13, находится в точке А(0, 4).
Пример 5. Найти глобальные экстремумы функции
ОТВЕТ. Целевая функция имеет два глобальных минимума, равных 17, в точках А(1, 4) и В(4, 1), глобальный максимум, равный 2417/49, достигается в точке Е(7, 4/7).
Дробно-линейное программирование
Дробно-линейное программирование относится к нелинейному программированию, так как имеет целевую функцию, заданную в нелинейном виде.
Задача дробно-линейного программирования в общем виде записывается следующим образом:
где — постоянные коэффициенты и
Рассмотрим задачу дробно-линейного программирования в виде
Для решения этой задачи найдём область допустимых решений, определяемую заданными ограничениями. Пусть эта область не является пустым множеством.
Из выражения, задающего целевую функцию, найдём х2:
Прямая x2 = kx1 проходит через начало координат. При некотором фиксированном значении L угловой коэффициент k тоже фиксирован, и прямая займёт определённое положение. При изменении значений L прямая x2 = kx1 будет поворачиваться вокруг начала координат.
Установим, как будет вести себя угловой коэффициент k при монотонном возрастании L. Найдём производную от k по L:
Знаменатель производной всегда положителен, а числитель от L не зависит. Следовательно, производная имеет постоянный знак, и при увеличении L угловой коэффициент будет только возрастать или только убывать, а прямая будет поворачиваться в одну сторону. Если имеет положительное значение, то прямая вращается против часовой стрелки, при отрицательном значении — по часовой стрелке. Установив направление вращения, находим вершину или вершины многогранника, в которых функция принимает max (min) значение, либо устанавливаем неограниченность задачи.
При этом возможны следующие случаи.
1. Область допустимых решений ограничена, максимум и минимум достигаются в её угловых точках (рис. а).
2. Область допустимых решений неограниченна, однако существуют угловые точки, в которых целевая функция принимает максимальное и минимальное значения (рис. б).
3. Область допустимых решений неограниченна, имеется один из экстремумов. Например, минимум достигается в одной из вершин области и имеет так называемый асимптотический максимум (рис. в).
4. Область допустимых решений неограниченна. Максимум и минимум являются асимптотическими (рис. г).
1 Классический медод решения задач нелинейного программирования
Математическая формулировка задачи принятия решения часто эквивалентна задаче отыскания экстремума функции одной или многих переменных. Поэтому для решения подобных задач могут быть использованы различные методы исследования функций классического анализа, в частности, методы поиска экстремума. Эти методы применяют в тех случаях, когда известен аналитический вид зависимости оптимизируемой функции Q от независимых переменныхuι.
1.1 Постановка задачи
В задаче нелинейного программирования требуется найти значение многомерной переменной х=(
), минимизирующее целевую функциюf(x) при условиях, когда на переменную х наложены ограничения типа неравенств
,i=1,2,…,m, а переменные
, т.е. компоненты вектора х, неотрицательны:
.
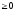
Иногда в формулировке задачи ограничения имеют противоположные знаки неравенств. Учитывая, однако, что если 
, то
, всегда можно свести задачу к неравенствам одного знака. Если некоторые ограничения входят в задачу со знаком равенства, например
, то их можно представить в виде пары неравенств
,
, сохранив тем самым типовую формулировку задачи.
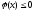
1.2 Экстремум функции одной переменной
Большинство простейших задач принятия решений эквивалентно задачам отыскания экстремума функции одной переменной.
Пусть требуется найти экстремум функции одной переменной Q (u) при отсутствии ограничений на диапазон изменения переменнойu.
Необходимым условием существования экстремума непрерывной функции Q (u) является равенство нулю первой производной (dQ /du = 0) или ее отсутствие. Графически равенство нулю производной означает, что касательная к кривойQ (u) в этой точке параллельна оси абсцисс (рис. 1.1,а), на рис. 1.1,бизображен случай, когда производные в точках экстремума не существуют.
Рисунок 1.1 –Различные типы экстремума функции одной переменной:
а – производная в точке экстремума существует;
б – производная в точке экстремума не существует.
Названные условия являются лишь необходимыми условиями. Их выполнение не означает еще, что в данных точках функция имеет экстремум (рис. 1.2).
Рисунок 1.2 –ФункцииQ(u), удовлетворяющие необходимым условиям экстремума:
а – производная равна нулю; б – производная не существует;
в – производная равна бесконечности
Для того, чтобы определить, действительно ли в исследуемой точке существует экстремум, необходимо проверить выполнение достаточных условий одним из методов, приведенных ниже.
1) Сравнение значений функций. Этот способ сводится к определению значений функции в точках, расположенных слева и справа в достаточной близости от исследуемой точки, т.е. в точках
где
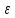
– малая положительная величина. Если
то в точкеu1 существует максимум (рис.1.3).
Если 
, то в точке u1 существует минимум (рис. 1.3, б). Если же Q(u1) будет занимать промежуточное между положение
например,
, то в точке u1 экстремума не будет (рис. 1.3,в).
Рисунок 1.3 –Проверка достаточных условий экстремума:
а – максимум;б – минимум;в – экстремума нет
2) Сравнение знаков производной. При этом способе определяется знак первой производной функции 
в точках
и
Если знаки производных различны, то в точкеu1 имеется экстремум функцииQ(u), причем, если при переходе от точки
к точке
знак производной изменяется с «+» на «–», то в точкеu1 – максимум (рис. 1.3,а). Если же знак меняется с «–» на «+», то в точкеu1 – минимум (рис. 1.3,б).
Если же знаки производных в точках 
и
одинаковы, то в точкеu1 экстремума нет (рис. 1.3,в).
3)Исследование знаков высших производных. Этот способ применяется в тех случаях, когда исследуемая функция имеет производные высших порядков. Если в точке u1 выполняется необходимое условие экстремума, т.е.
и существует вторая производная –
, значение которой вычисляется в «подозреваемой» точке u1, то точка u1 является точкой максимума, если
< 0, и точкой минимума, если
.
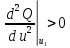
Если же 
, то для дальнейших исследований вычисляются 
и т.д.
При решении практических задач, как правило, приходится исследовать функции, имеющие несколько экстремумов. В этом случае говорят о нахождении наибольшего и наименьшего значения функции, которые называют глобальными экстремумами. Остальные экстремумы называются локальными. Также в практических задачах диапазон изменения переменной u часто бывает ограничен заданным интервалом [a,b], поэтому в число «подозреваемых» точек должны быть включены и крайние точки этого интервала, так как в них может достигаться глобальный экстремум.
Общая постановка задачи нелинейного программирования (ЗНП).
Задача нелинейного программирования встречается в естественных науках, технике, экономике, математике, в сфере деловых отношений и в науке управления государством.
Нелинейное программирование, например, связано с основной экономической задачей. Так в задаче о распределении ограниченных ресурсов максимизируют либо эффективность, либо, если изучается потребитель, потребление при наличии ограничений, которые выражают условия недостатка ресурсов. В такой общей постановке математическая формулировка задачи может оказаться невозможной, но в конкретных применениях количественный вид всех функций может быть определен непосредственно. Например, промышленное предприятие производит изделия из пластмассы. Эффективность производства здесь оценивается прибылью, а ограничения интерпретируются как наличная рабочая сила, производственные площади, производительность оборудования и т.д.
Метод «затраты — эффективность» также укладывается в схему нелинейного программирования. Данный метод был разработан для использования при принятии решений в управлении государством. Общей функцией эффективности является благосостояние. Здесь возникают две задачи нелинейного программирования: первая — максимизация эффекта при ограниченных затратах, вторая — минимизация затрат при условии, чтобы эффект был выше некоторого минимального уровня. Обычно эта задача хорошо моделируется с помощью нелинейного программирования.
Результаты решения задачи нелинейного программирования являются подспорьем при принятии государственных решений. Полученное решение является, естественно, рекомендуемым, поэтому необходимо исследовать предположения и точность постановки задачи нелинейного программирования, прежде чем принять окончательное решение.
Задачи нелинейного программирования часто возникают и в других отраслях науки. Так, например, в физике целевой функцией может быть потенциальная энергия, а ограничениями — различные уравнения движения. В общественных науках и психологии возникает задача минимизации социальной напряженности, когда поведение людей ограничено определенными законами.
КЛАССИЧЕСКИЙ МЕДОД РЕШЕНИЯ ЗАДАЧ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Математическая формулировка задачи принятия решения часто эквивалентна задаче отыскания экстремума функции одной или многих переменных. Поэтому для решения подобных задач могут быть использованы различные методы исследования функций классического анализа, в частности, методы поиска экстремума. Эти методы применяют в тех случаях, когда известен аналитический вид зависимости оптимизируемой функции Q от независимых переменных u?.
Постановка задачи
В задаче нелинейного программирования требуется найти значение многомерной переменной х=(), минимизирующее целевую функцию f(x) при условиях, когда на переменную х наложены ограничения типа неравенств, i=1,2,…,m, а переменные, т.е. компоненты вектора х, неотрицательны:
Иногда в формулировке задачи ограничения имеют противоположные знаки неравенств. Учитывая, однако, что если, то, всегда можно свести задачу к неравенствам одного знака. Если некоторые ограничения входят в задачу со знаком равенства, например, то их можно представить в виде пары неравенств, сохранив тем самым типовую формулировку задачи.
Общая постановка задачи нелинейного программирования (ЗНП).
gi(X) = bi (1 ≤ i ≤ k),
gi(X) ≤ bi (k+1 ≤ i ≤m),
где Х= (x1, x2, …,xn)
Определить max(min) целевой функции Z= f(Х) при заданной системе ограничений, где хотя бы одна из указанных функций нелинейная.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: